1.2. Основные понятия теории множеств и 1.3. Основные структуры. 2

1.4. Перестановки. 3

1.5. Размещения. 4

1.6. Сочетания. 5

2.1. Классическое определение вероятности. 5

2.2. Теоремы сложения и умножения вероятностей. 5

2.3. Дискретные случайные величины. 5

2.4. Нормальный закон распределения вероятностей. 7

2.5. Основные понятия теории вероятности. 8

2.6. Аксиомы теории вероятности. 9

3.1. Дифференциальное исчисление функции одной переменной 9

3.2. Разрыв функции. 11

3.3. Функция. График. 14

3.4. Понятие дифференциального уравнения 18

4.1. Языки программирования высокого уровня 18

4.2. Задачи на циклы с параметром. 21

4.3. Алгоритмы 22

4.4. Работа с заданными массивами. 24

4.5. Блок – схемы. Ветвление. 26

4.6. Блок – схемы. Циклы с проверкой условия. 27

Текстовые редакторы. Таблицы 28

Электронные таблицы. Встроенные функции. 28

5.3. Компьютерная графика 29

5.4. Служебные программы. 31

5.7. Основные компоненты операционных систем. 32

5.8. Обзор программного обеспечения. 36

Двоичная система счисления. 36

Представление чисел в различных системах счисления 38

Система счисления 38

6.2 Количество информации. 39

Интернет 39

Адресация в Интернет 43

Способы подключения к Интернету 45

Защита информации. Шифрование. 45

Кодирование информации 54

1.1. АКСИОМАТИЧЕСКИЙ МЕТОД — способ построения на­учной теории (обладающей одной и той же синтаксической структурой), при котором в основу теории кладутся неко­торые исходные положения, называемые аксиомами тео­рии, а все остальные предложения теории получаются как логические следствия аксиом.

Основу построения научной теории составляют аксиомы - основное положение, не требующее доказательства. Остальные утверждения( например, теоремы) извлекаются из системы аксиом путем логических доказательств.

Дополнительно:

В математике аксиоматический метод зародился в работах древнегреческих геометров. Блестящим образцом применения аксиоматический метод вплоть до 19 в. была геометрическая система, известная под названием «Начал» Евклида (около 300 до н. э.). Хотя в то время не вста­вал ещё вопрос об описании логических средств, применяемых для извлечения содержательных следствий из аксиом, в системе Евклида уже достаточно чётко проведена идея получения всего основного содержания геометрической тео­рии чисто дедуктивным путём, из некоторого, относительно небольшого, числа утверждений — аксиом, истинность которых представлялась наглядно очевидной.

Открытие в начале 19 в. неевклидовой геометрии Н. И. Лобачевским и Я. Больяй явилось толчком к дальнейшему развитию аксиоматического метода. Они установили, что, заменив привычный и, казалось бы, единственно «объективно истинный» пятый постулат Евклида о параллельных его отрицанием, можно, развивать чисто логическим путём геометрическую теорию, столь же стройную и богатую содержанием, как и геометрия Евклида. Этот факт заставил математиков 19 в. обратить специальное внимание на дедуктивный способ построения математической теорий, что повлекло за собой возникновение связанной с самим понятием аксиоматического метода и формальной (аксиоматической) математической теории новой проблематики, на основе которой выросла так называемая теория доказательств как основной раздел современной математической логики. Понимание необходимости обоснования математики и конкретные задачи в этой области зародились в более или менее отчётливой форме уже в 19 в. Уточнение основных понятий анализа и сведение более сложных понятий к простейшим на точной и логически всё более строгой осно­ве, а также открытие неевклидовых геометрий стимулировали развитие аксиоматического метода и возникновение проблем более общего математического. характера, таких, как непротиворечивость, полнота и независимость той или иной системы аксиом.

1.2. Основные понятия теории множеств и 1.3. Основные структуры.

Множество – это набор, совокупность, собрание каких-либо объектов, называемых его элементами, обладающими общим для всех них характеристическим свойством.

Обозначения: М – множество (принято обозначать заглавными латинскими буквами),

x M – элемент x принадлежит множеству М,

М = {x₁, x₂, x₃, … , x_n} – множество М состоит из элементов x_i, где i =1…n,

M = {Ø} – множество М – пустое, т.е. не содержит элементов,

А В – множество А является подмножеством множества В, т.е. все элементы множества А являются одновременно элементами множества В.

А = В – множество А равно множеству В, т.е. множество А является подмножеством множества В, а множество В является подмножеством множества А.

Способы задания множеств

1. Перечисление элементов – самый простой способ задания множества. Примером может служить список имен студентов, присутствующих на занятии.

2. Аналитический способ предполагает описание характеристического свойства множества. Пусть Р(x) – некоторое предложение, зависящее от x. Тогда запись А = {x | P(x)}, говорит о том, что множество А состоит из всех элементов x, обращающих в истинное утверждение P(x). Например, А = {x | x N} – множество, всех натуральных чисел или В = {x | x - это студент} – множество всех студентов.

3. Графический. Множество может задаваться графически. Например, А и В – множества точек круга и отрезка, соответственно:

Операции над множествами

Суммой или объединением нескольких множеств называется множество всех элементов, которые являются элементами хотя бы одного из исходных множеств. Обозначается А В.

Пример. Если А = {1,2,4,7,8} и В = {1,3,5,6,9}, тогда А В = {1,2,3,4,5,6,7,8,9}.

Пересечением множеств называется множество, состоящее из общих элементов исходных множеств. Обозначается А В.

Пример. Если А = {1,2,4,7,8} и В = {1,2,5,6,9}, тогда А В = {1,2}.

Разностью двух множеств А и В называется множество, состоящее из элементов множества А, не принадлежащих множеству В. Обозначается А\В.

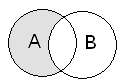
Пример. Если А = {1,2,4,7,8} и В = {1,3,5,6,9}, тогда А\В = {2,4,7,8}.

Разность между множеством В и его частью - множеством А, называется дополнением множества А до множества В. Обозначается .

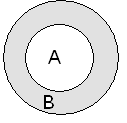
Пример. Если А = {1,2,4} и В = {1,2,4,6,8,10}, тогда = {6,8,10}.

Разбиением множества А называется такая расчлененная система U непустых подмножеств множества А, что каждый элемент А является элементом некоторого (единственного) множества системы U.

Пример. U = {{1},{2, 4},{7},{8}} – разбиение множества А = {1,2,4,7,8}.

1.4. Перестановки.

Пусть А — некоторое конечное множество, состоящее из п различных элементов;

A — {a_l; а₂; а₃;...; а_п}. (I)

Будем образовывать из элементов множества А упорядоченные множества. В качестве первого упорядоченного множества возьмем множество, в котором элементы расположены в порядке возрастания их номеров:

{a_l; а₂; а₃;...; а_п}

Второе упорядоченное множество можно образовать, поменяв местами элементы а₁ и а₂, а все остальные элементы первого множества оставив на своих местах:

{ а₂; a_l; а₃;...; а_п}

Поменяв местами элементы а₂ и а₃ оставляя на своих местах все остальные элементы в первом упорядоченном множестве, получаем упорядоченное множество, отличное как от первого, так и от второго упорядоченного множества. Аналогичным способом из элементов множества А можно строить и другие упорядоченные множества.

Всевозможные конечные упорядоченные множества, содержащие п различных элементов, которые можно получить из некоторого не­упорядоченного множества, состоящего из п различных элементов, называются перестановками из n элементов.

Таким образом, перестановка есть не что иное, как способ упорядо­чивания элементов некоторого конечного множества. При этом любые две различные перестановки представляют собой два различных спо­соба образования упорядоченного множества (из данного неупорядо­ченного множества).

Число перестановок из п элементов (которое обычно обозначается Р_п) равно произведению п последовательных натуральных чисел, начиная с единицы. Это произведение имеет специальное обозна­чение n! (читается: n факториал):

Р_п= 1*2*3*...* (n— 1)*n = n!

Для пустого множества принимается соглашение: пустое мно­жество можно упорядочить только одним способом; поэтому считается, что

Ø! = 1.

Если в заданной перестановке поменять местами какие-либо два элемента, а все остальные элементы оставить на своих местах, то полу­чится новая перестановка.

Такое преобразование перестановки называется транспозицией.

Все n!перестановок из n элементов можно расположить в таком порядке, что каждая следующая перестановка будет излучаться из предыдущей одной транспозицией, причем в качестве исходной пере­становки можно выбрать любую из n! перестановок. В частности, от любой перестановки из n элементов можно перейти к любой другой перестановке из тех же элементов при помощи нескольких транспо­зиций.

Перестановки с повторениями. Пусть А — некоторая со­вокупность, состоящая из п элементов: А= {a_l; а₂; а₃;...; а_п}

т различных типов (m n), причем элементы одного типа, неразли­чимы между собой, И пусть k₁ элементов принадлежат первому типу, k₂ элементов принадлежат второму типу, k ₃ — третьему, k_m — m-му типу, причем k₁+k₂+k₃+…+k_m= n.

Например, если A = {1, 1, 2, 3, 1, 3}, то, считая элементами первого типа единицы, элементами второго типа двойки, а элементами третьего типа тройки, имеем

k₁ = 3, k₂ = 1, k₃=2.

Различные конечные совокупности, содержащие п элементов, из которых k₁ принадлежат первому типу, k₂ — второму типу . . ., k_m — m-му, типу, называются перестановками с повторениями (кортежами), имеющими состав (или спецификацию) (k_1,k_2,k_3,…,k_m).

Число таких различных перестановок с повторениями обычно обо­значается С_п (k_1,k_2,k_3,…,k_m)

и вычисляется по формуле

С_п (k_1,k_2,k_3,…,k_m)=