
- •Оглавление
- •Введение
- •Указания по выполнению лабораторных работ
- •Правила техники безопасности в учебнох лабораториях
- •Глава 1. Механика Лабораторная работа №1 статистическая обработка результатов измерений
- •Введение
- •3. Вычисляем среднее значение:
- •5. Вычисляем среднеквадратичное отклонение:
- •7. Вычисляем абсолютную ошибку измерения:
- •Для полной характеристики точности эксперимента определяют кроме абсолютной ошибки еще и относительную ошибку эксперимента, которую выражают зачастую в относительных процентах:
- •2. Записываем расчетную формулу:
- •И выводим формулу для вычисления абсолютной ошибки:
- •6. По формуле (5) вычисляем относительную ошибку.
- •Порядок выполнения работы
- •Лабораторная работа №2 скатывание тела по наклонной плоскости
- •Введение Движение тела в поле силы подчиняется второму закону Ньютона:
- •При равенстве нулю начальной скорости и координаты уравнения (1) примут вид
- •Описание установки
- •Порядок выполнения работы
- •8. Вычислить (и записать в шестую строку) шесть моментов времени tcpi, с которыми ассоциируются величины Vcpi:
- •Результаты эксперимента по изучению равноускоренного движения
- •Лабораторная работа №3 скольжение тела по наклонной плоскости
- •Введение
- •И соответственно:
- •Из полученного выражения выразим коэффициент трения скольжения:
- •Порядок выполнения работы
- •7. Вычислить и занести в таблицу значения изменения скорости ∆VI и ускорения ai по формулам:
- •Лабораторная работа №4 движение тел вращения по наклонной плоскости
- •Введение
- •С учетом того, что уравнение (13) перепишем в виде:
- •Порядок выполнения работы
- •Результаты эксперимента по определению потерь на вращение
- •11. Вычислить и занести в таблицу значения скорости тела VI и коэффициентов потерь энергии на вращение по формулам:
- •Лабораторная работа №5 поступательное движение тела в гравитационном поле земли
- •Введение
- •В общем случае для тела находящегося на поверхности Земли можно считать, что сила тяжести и сила гравитационного тяготения равны между собой:
- •Равноускоренное движение характеризуется линейным изменением скорости и параболическим изменением пройденного пути со временем: :
- •Описание установки
- •Измеренные с помощью датчиков временных интервалов средние скорости v1 и v2 вычисляются:
- •Порядок выполнения работы
- •Лабораторная работа №6 неупругий удар двух тел
- •Введение
- •Порядок выполнения работы
- •Результаты измерений временных интервалов
- •Результаты расчета скоростей и погрешности эксперимента
- •Лабораторная работа №7 механические колебания маятника
- •Введение
- •Описание экспериментальной установки
- •Порядок выполнения работы
- •Результаты эксперимента по определению периода колебаний маятника
- •Изучение малых колебаний маятника
- •Описание установки
- •Методика измерений момента инерции
- •Порядок выполнения работы
- •Лабораторная работа №9 определение скорости «пули» с помощью крутильно-баллистического маятника
- •Описание установки
- •Методика измерений
- •Порядок выполнения работы
- •Лабораторная работа №10 изучение основного уравнения динамики вращательного движения на маятнике обербека
- •Введение
- •Методика измерений
- •Описание установки
- •Порядок выполнения работы
- •Лабораторная работа №11 определение момента инерции маятника максвелла
- •Введение
- •Методика измерений
- •Описание экспериментальной установки
- •Порядок выполнения работы
- •Методика измерений
- •Порядок выполнения работы
- •Лабораторная работа № 13 изучение колебаний связанных маятников
- •Введение
- •Описание экспериментальной установки
- •Порядок выполнения работы
- •Глава 2. Электричество Лабораторная работа № 14 закон ома для участка цепи
- •Введение
- •Описание экспериментальной установки
- •Порядок выполнения работы
- •Порядок выполнения работы
- •Лабораторная работа № 16 Изучение зависимости сопротивления металла от температуры
- •Введение
- •Методика измерений
- •Описание экспериментальной установки
- •Порядок выполнения работы
- •Лабораторная работа № 17. Определение удельного сопротивления проводника
- •Описание экспериментальной установки
- •Лабораторная работа № 18 Закон Ома для полной цепи. Определение емкости химического источника тока
- •Введение
- •Описание экспериментальной установки
- •Порядок выполнения работы
Лабораторная работа №9 определение скорости «пули» с помощью крутильно-баллистического маятника
Цель работы: определить момент инерции маятника, модуль кручений проволоки и скорость «пули».
Описание установки
Лабораторная работа, схема установки которой приведена на рис. 7, проводится на крутильно-баллистическом маятнике. Крутильно-баллистический маятник представляет собой тело, с большим моментом инерции J, подвешенное на упругой нити, которая является его осью вращения.



 3
3
1 2



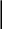

 4
4



l l


1 – первый груз маятника;
2 – второй груз маятника, в который выстреливают «пулей»;
3 – проволока подвеса маятника;
4 – фотодатчик, для измерения периода колебаний маятника/
Рис. 7. Схема установки для определения момента инерции маятника
Маятник выполнен в виде горизонтальной крестовины с двумя грузами 1 и 2 массы m0 каждый. Во второй груз выстреливают из пружинного пистолета «пулей», ствол которого перпендикулярен плоскости мишени. «Пуля» застревает во втором грузе. В установке отсчёт времени и числа колебаний маятника начинается по сигналу фотоэлемента после нажатия клавиши “сброс”, когда флажок маятника пересечёт световой луч фотоэлемента. Счёт времени заканчивается после нажатия клавиши “стоп” в момент окончания очередного колебания.
Методика измерений
Период
гармонических крутильных колебаний
маятника зависит от его момента инерции
![]() и модуля кручения k
проволоки подвески маятника (для данного
маятника k
– постоянная величина):
и модуля кручения k
проволоки подвески маятника (для данного
маятника k
– постоянная величина):
|
(38) |
где J0 – момент инерции крестовины маятника; m0 – масса груза; l – расстояние от центра груза до оси вращения.
Представим уравнение (38) в виде линейной зависимости T2 от l2
|
(39) |
По
этому уравнению экспериментальной
зависимости
![]() можно определить момент инерции
крестовины J0
и модуль кручения проволоки k.
можно определить момент инерции
крестовины J0
и модуль кручения проволоки k.
Маятник
перед ударом «пули» покоится (момент
упругих сил подвески относительно оси
вращения равен нулю). Для системы
«пуля-маятник» выполняется закон
сохранения момента импульса (момент
импульса пули до удара
![]() передаётся в момент удара маятнику):
передаётся в момент удара маятнику):
|
(40) |
где
m
и v
– масса и скорость «пули»; r
– расстояние от оси маятника до места
застревания «пули» в грузе 2;
![]() –момент
инерции маятника (с застрявшей в нем
пулей) относительно оси вращения
маятника; ω –
угловая скорость маятника сразу после
удара «пули».
–момент
инерции маятника (с застрявшей в нем
пулей) относительно оси вращения
маятника; ω –
угловая скорость маятника сразу после
удара «пули».
Можно принять расчетную формулу момента
инерции пули
![]() ,
т.е. момент инерции пули определяется
в приближении материальной точки. Тогда
расчетная формула для скорости «пули»
следующая:
,
т.е. момент инерции пули определяется
в приближении материальной точки. Тогда
расчетная формула для скорости «пули»
следующая:
|
(41) |
Массу
«пули» m
и расстояние r
от оси вращения до точки удара «пули»
определяют прямыми измерениями, а момент
инерции маятника J
и его начальную угловую скорость
![]() после удара «пули» – косвенно.
после удара «пули» – косвенно.
После удара «пули» маятник совершает крутильные колебания, которые, при малом сопротивлении воздуха, можно считать гармоническими:
|
(42) |
где
![]() – максимальный угол отклонения маятника
после попадания в него пули;
– максимальный угол отклонения маятника
после попадания в него пули;
![]() – циклическая частота собственных
колебаний маятника; Т
– период этих колебаний.
– циклическая частота собственных
колебаний маятника; Т
– период этих колебаний.
Дифференцируя (42) по времени, получаем формулу угловой скорости маятника:
|
|
Сразу
после удара «пули» угловая скорость
маятника максимальная и равна амплитуде
угловой скорости (![]() ),
которую выразим через период колебаний:
),
которую выразим через период колебаний:
|
(43) |

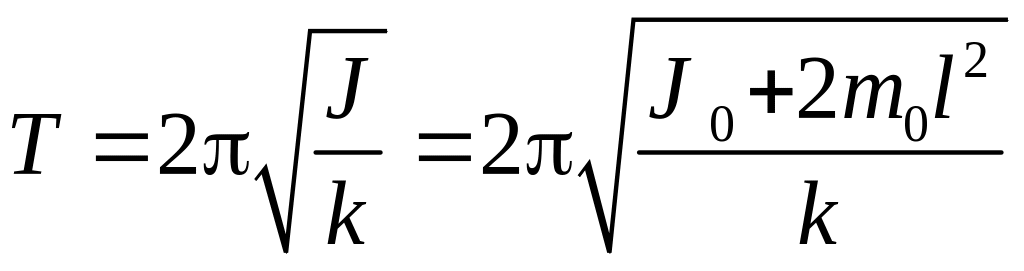

 .
.