
- •6. Функциональный ряд — ряд, каждым членом которого, в отличие от числового ряда, является не число, а функция .
- •Признак Вейерштрасса (мажорантный признак)
- •7. Степенным рядом назовем ряд вида cn(z-z0)n, z0 -центр,
- •8. На любом отрезке целиком лежащем внутри интервала сходимости степенного ряда, сумма ряда есть непрерывная функция.
- •Арифметические операции над степенными рядами.
- •Ряды Тейлора и Маклорена
1.(Понятие
числового ряда)Пусть числа ![]() - члены
некоторой бесконечной числовой
последовательности. Тогда выражение
вида
- члены
некоторой бесконечной числовой
последовательности. Тогда выражение
вида ![]() :(1)
называется числовым рядом. Здесь
:(1)
называется числовым рядом. Здесь ![]() -
общий член ряда (1). Ряд (1) называется
сходящимся, если последовательность
его частичных сумм
-
общий член ряда (1). Ряд (1) называется
сходящимся, если последовательность
его частичных сумм :(2)
имеет конечный предел. Этот
предел
:(2)
имеет конечный предел. Этот
предел 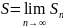 называется
суммой ряда. Если последовательность
частичных сумм (2) расходится, то ряд
(1) называется расходящимся. Основные
свойства сходства рядов:
называется
суммой ряда. Если последовательность
частичных сумм (2) расходится, то ряд
(1) называется расходящимся. Основные
свойства сходства рядов:
1°. Отбрасывание конечного числа членов не влияет на сходимость ч.р.
Рассмотрим
 и
и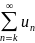 .
Пусть
.
Пусть![]()
![]() тогда
тогда
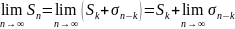 (3).
Если существует конечный предел справа
в (3) то существует и предел слева, и ряд
сходится
(3).
Если существует конечный предел справа
в (3) то существует и предел слева, и ряд
сходится
2°.
Если ряд
сходится
и имеет сумму S, то ряд ,с
= const, сходится и имеет сумму cS.
,с
= const, сходится и имеет сумму cS.
Пусть![]() тогда
тогда
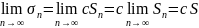 .
.
3°.
Если ряды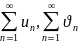 сходятся и имеют суммы
сходятся и имеют суммы  соответственно,
то ряд
соответственно,
то ряд
 сходится
и имеет сумму
сходится
и имеет сумму
 Пусть
Пусть![]()
![]() тогда
тогда
 .
.
Геометрич прогрессия. последовательность чисел {an} называется
геометрической
прогрессией,
если отношение последующего члена к
предыдущему равно одному и тому же
постоянному числу q,
называемому знаменателем
геометрической прогрессии.
Таким образом, ![]() для
всех членов геометрической прогрессии.
Предполагается, что q
≠ 0 и q
≠ 1.
Любой
член геометрической прогрессии можно
вычислить по формуле:
для
всех членов геометрической прогрессии.
Предполагается, что q
≠ 0 и q
≠ 1.
Любой
член геометрической прогрессии можно
вычислить по формуле:![]() .
.![]() - этим выражением определяется сумма
первых n членов геометрической прогрессии
- этим выражением определяется сумма
первых n членов геометрической прогрессии
определяется
выражением. Говорят,
что бесконечная геометрическая
прогрессия сходится,
если предел 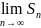 существует
и конечен.
В
противном случае
прогрессия расходится.
Пусть
существует
и конечен.
В
противном случае
прогрессия расходится.
Пусть ![]() представляет
собой бесконечный ряд геометрической
прогрессии. Данный ряд сходится к
представляет
собой бесконечный ряд геометрической
прогрессии. Данный ряд сходится к 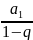 ,
если знаменатель |q|
< 1, и расходится, если знаменатель |q|
> 1.
,
если знаменатель |q|
< 1, и расходится, если знаменатель |q|
> 1.
2.
Ряд сходится, если S конечно;
тогда 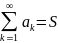 .
Необходимое условие сходимости ряда:
.
Необходимое условие сходимости ряда: 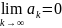 .
В математике гармонический ряд
.
В математике гармонический ряд
представляет
собой сумму, составленную из бесконечного
количества членов, обратных последовательным
числам натурального
ряда:![]() .
Достаточные
признаки сходимости
.
Достаточные
признаки сходимости
числовых рядов с положительными членами.
Теорема 1 (признак сравнения). Если члены двух числовых рядов
и  удовлетворяют
неравенству
удовлетворяют
неравенству для
любых n,
то из сходимости второго
ряда следует сходимость первого ряда.
Из расходимости первого ряда следует
расходимость второго ряда.
для
любых n,
то из сходимости второго
ряда следует сходимость первого ряда.
Из расходимости первого ряда следует
расходимость второго ряда.
3.(Признак
Даламбера)
(возьмем дробь за (1) )
Допустим, что строго положительный ряд
a1 + a1q + a1q2 + a1q3 +
... таков, что существует (конечный
или бесконечный) предел
за (1) )
Допустим, что строго положительный ряд
a1 + a1q + a1q2 + a1q3 +
... таков, что существует (конечный
или бесконечный) предел
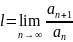 .
Тогда при l >
1 ряд a1 + a2 + a3 +
... an
расходится,
а при L <
1 сходится.
Допустим
сначала, что L >
1. Так как дробь (1) стремится к L,
то достаточно далекие значения этой
дроби будут удовлетворять неравенству
(1)>1. Пусть,
например, это неравенство выполнено
для всех n,
удовлетворяющих неравенству n > m.
Тогда ряд am+1 + am+2 + am+3 +
... таков,
что у него отношение уже любого
последующего члена к своему предыдущему
оказывается удовлетворяющим неравенству
(1)>1 Значит по лемме
1:
(Если строго положительный ряд
a1 + a2 + a3 +
... an
таков,
что при всех n оказывается
(1)>1, то этот ряд расходится), ряд
am+1 + am+2 + am+3 +
... а так как это есть остаток ряда
a1 + a2 + a3 +
... an
то
этот последний ряд также расходится.
Пусть
теперь l <
1.
Закрепим какое-нибудь число q
,удовлетворяющее
неравенству l < q <
1 (например, положим
.
Тогда при l >
1 ряд a1 + a2 + a3 +
... an
расходится,
а при L <
1 сходится.
Допустим
сначала, что L >
1. Так как дробь (1) стремится к L,
то достаточно далекие значения этой
дроби будут удовлетворять неравенству
(1)>1. Пусть,
например, это неравенство выполнено
для всех n,
удовлетворяющих неравенству n > m.
Тогда ряд am+1 + am+2 + am+3 +
... таков,
что у него отношение уже любого
последующего члена к своему предыдущему
оказывается удовлетворяющим неравенству
(1)>1 Значит по лемме
1:
(Если строго положительный ряд
a1 + a2 + a3 +
... an
таков,
что при всех n оказывается
(1)>1, то этот ряд расходится), ряд
am+1 + am+2 + am+3 +
... а так как это есть остаток ряда
a1 + a2 + a3 +
... an
то
этот последний ряд также расходится.
Пусть
теперь l <
1.
Закрепим какое-нибудь число q
,удовлетворяющее
неравенству l < q <
1 (например, положим ![]() ).
Тогда найдется такое m,
что при всех n > m будет
(1)<q.
Снова составляя ряд am+1 + am+2 + am+3 +
..
и
применяя к нему лемму
2:
(Если строго положительный ряд
a1 + a2 + a3 +
... an
таков, что при всех n оказывается
(1) <= q
где q -
некоторое постоянное число, меньшее
единицы, 0 < q <
1, то этот ряд сходится.)
убеждаемся
сначала в сходимости ряда
am+1 + am+2 + am+3 +
... а затем и ряда
a1 + a2 + a3 +
... an.(Радикальный
признак Коши)
Если
для числового ряда
с неотрицательными членами существует
такое число
).
Тогда найдется такое m,
что при всех n > m будет
(1)<q.
Снова составляя ряд am+1 + am+2 + am+3 +
..
и
применяя к нему лемму
2:
(Если строго положительный ряд
a1 + a2 + a3 +
... an
таков, что при всех n оказывается
(1) <= q
где q -
некоторое постоянное число, меньшее
единицы, 0 < q <
1, то этот ряд сходится.)
убеждаемся
сначала в сходимости ряда
am+1 + am+2 + am+3 +
... а затем и ряда
a1 + a2 + a3 +
... an.(Радикальный
признак Коши)
Если
для числового ряда
с неотрицательными членами существует
такое число ![]() ,
, ![]() ,
что, начиная с некоторого номера,
выполняется неравенство
,
что, начиная с некоторого номера,
выполняется неравенство ![]() ,
то данный ряд сходится. Условие
радикального признака равносильно
следующему:
,
то данный ряд сходится. Условие
радикального признака равносильно
следующему:
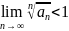 ,
то есть можно сформулировать радикальный
признак сходимости знакоположительного
ряда в предельной форме:
Если
для ряда
,
то есть можно сформулировать радикальный
признак сходимости знакоположительного
ряда в предельной форме:
Если
для ряда
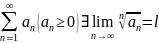 ,
то если
,
то если ![]() ряд
сходится, если
ряд
сходится, если ![]() ряд
расходится, если
ряд
расходится, если ![]() вопрос
о сходимости ряда остается открытым.
вопрос
о сходимости ряда остается открытым.
4.(Интегральный
признак)
Пусть данный ряд имеет вид  причем f (n)
есть значение в точке x = n некоторой
функции f (x),
определенной при x ≥ n0.
Если f(x)
монотонно убывает и в области определения
справедливо неравенство f (x)
≥ 0, то ряд
сходится тогда и только тогда, когда
сходится несобственный интеграл
причем f (n)
есть значение в точке x = n некоторой
функции f (x),
определенной при x ≥ n0.
Если f(x)
монотонно убывает и в области определения
справедливо неравенство f (x)
≥ 0, то ряд
сходится тогда и только тогда, когда
сходится несобственный интеграл 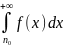 .
.
5.(Знакочередующиеся
ряды) Ряд называется знакочередующимся,
если его члены попеременно принимают
значения противоположных знаков, т. е.:
![]() .
.
Признак
Лейбница —
признак сходимости знакочередующегося
ряда, установлен Готфридом
Лейбницем.
Формулировка теоремы: Пусть для
знакочередующегося ряда
выполняются
следующие условия:1.![]() (монотонное
невозрастание {an}
по абсолютной
величине)2.
(монотонное
невозрастание {an}
по абсолютной
величине)2.![]() .Тогда
этот ряд сходится.
.Тогда
этот ряд сходится.
Знакопеременные ряды. Числовой ряд, содержащий бесконечное множество положительных и бесконечное множество отрицательных членов, называется знакопеременным. Частным случаем знакопеременного ряда являетсязнакочередующийся ряд, то есть такой ряд, в котором последовательные члены имеют противоположные знаки.
Признак абсолютной сходимости. Понятие условной сходимости.
Ряд
называется абсолютно
сходящимся,
если ряд  также
сходится. Если
ряд
сходится
абсолютно, то он является сходящимся
(в обычном смысле). Обратное утверждение
неверно.
Ряд
называется условно
сходящимся,
если сам он сходится, а ряд, составленный
из модулей его членов, расходится.
также
сходится. Если
ряд
сходится
абсолютно, то он является сходящимся
(в обычном смысле). Обратное утверждение
неверно.
Ряд
называется условно
сходящимся,
если сам он сходится, а ряд, составленный
из модулей его членов, расходится.
6. Функциональный ряд — ряд, каждым членом которого, в отличие от числового ряда, является не число, а функция .
(Понятие
равномерной сходимости для функциональной
последовательности и ряда.)Существует
функция ![]() такая,
что:
такая,
что: ![]() .Факт
равномерной сходимости последовательности
к
функции
.Факт
равномерной сходимости последовательности
к
функции ![]() записывается:
записывается: ![]()
Мажорируемые ряды. если каждый член положительного ряда не больше, чем имеющий тот же номер член другого ряда, то второй ряд называется мажорантным по отношению к первому.Иначе говоря, ряд b1 + b2 + b3 + ... является мажорантным по отношению к ряду a1 + a2 + a3+..,
если при всех n будет an ≤ bn.
Признак Вейерштрасса (мажорантный признак)
и
если
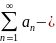 сходится,
то функциональный ряд
сходится,
то функциональный ряд 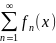 сходится
равномерно на Е. Доказательство (по
критерию Коши).
сходится
равномерно на Е. Доказательство (по
критерию Коши).
![]()
7. Степенным рядом назовем ряд вида cn(z-z0)n, z0 -центр,
cn - коэффициенты - заданные комплексные числа. При z= z0 ряд очевидно сходится. Это может быть единственная точка сходимости Sn!zn, а также ряд может сходится на всей комплексной плоскости Szn/n!. При исследовании степенного ряда важно установить область его равномерной сходимости. Как будет показано далее, область сходимости степенного ряда определяется видом его коэффициентов cn.
Теорема Абеля. Если степенной ряд Scn(z-z0)n сходится в точке z1 ¹ z0 , то он абсолютно сходится и при " z: |z-z0|<|z1-z0 |, причем в замкнутом круге |z-z0|£r<|z1-z0| сходится равномерно
Интервал
и радиус сходимости Рассмотрим
функцию![]() .
Ее областью определения является
множество тех значений x,
при которых ряд сходится. Область
определения такой функции
называется интервалом
сходимости.
Если
интервал сходимости представляется в
виде
.
Ее областью определения является
множество тех значений x,
при которых ряд сходится. Область
определения такой функции
называется интервалом
сходимости.
Если
интервал сходимости представляется в
виде ![]() ,
где
,
где
R > 0, то величина R называется радиусом сходимости.
8. На любом отрезке целиком лежащем внутри интервала сходимости степенного ряда, сумма ряда есть непрерывная функция.
(Почленное
интегрирование степенного ряда). Если
пределы интегрирования лежат внутри
интервала сходимости степенного
ряда, то последовательность интегралов от
частичных сумм ряда сходится к интегралу
от суммы ряда.
(Почленное дифференцирование степенного
ряда).Пусть
степенной ряд![]() (2.1)
(2.1)
имеет
радиус сходимости R.
Тогда ряд![]()
(2.2)
полученный
в результате почленного дифференцирования
ряда (2.1), также имеет радиус
сходимости R. Производная
суммы ряда (2.1) равна сумме ряда
(4.2): 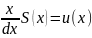 . Степенной
ряд в пределах его интервала сходимости
можно дифференцировать почленно любое
число раз. При этом радиусы сходимости
всех рядов, полученных дифференцированием
данного ряда, совпадают с радиусом
сходимости этого ряда.
. Степенной
ряд в пределах его интервала сходимости
можно дифференцировать почленно любое
число раз. При этом радиусы сходимости
всех рядов, полученных дифференцированием
данного ряда, совпадают с радиусом
сходимости этого ряда.
Наряду
со степенными рядами вида![]()
Арифметические операции над степенными рядами.
1![]() )
Интегрирование степенных рядов.
)
Интегрирование степенных рядов.
Если некоторая функция
f(x) определяется - степенным рядом, то интеграл от этой функции можно записать в виде ряда:
![]() 2)
Дифференцирование степенных
рядов.Производная
функции, которая определяется степенным
рядом, находится по формуле:
2)
Дифференцирование степенных
рядов.Производная
функции, которая определяется степенным
рядом, находится по формуле:
![]()
3) Сложение, вычитание, умножение и деление степенных рядов. Сложение и вычитание степенных рядов сводится к соответствующим операциям с их членами:
![]() П
П![]() роизведение двух
степенных рядов выражается формулой:
роизведение двух
степенных рядов выражается формулой:![]()
Коэффициенты сi находятся по формуле:
![]()
Д![]() еление двух
степенных рядов выражается формулой:
еление двух
степенных рядов выражается формулой:
Для определения коэффициентов
qn рассматриваем произведение
![]() ,
полученное из записанного выше равенства
и решаем систему уравнений:
,
полученное из записанного выше равенства
и решаем систему уравнений:

9.Разложение
функций в степенные ряды Пусть
дана функция f(x),
которую требуется разложить в степенной
ряд, т.е. представить в виде
![]() (30):
Задача состоит в определении
коэффициентов
(30):
Задача состоит в определении
коэффициентов ![]() ряда
(30). Для этого, дифференцируя равенство
(30) почленно, последовательно найдём:
ряда
(30). Для этого, дифференцируя равенство
(30) почленно, последовательно найдём:
![]()
![]()
![]() (31)
(31)![]() Полагая
в равенствах (30) и (31) х =
0, находим
Полагая
в равенствах (30) и (31) х =
0, находим
![]()
![]()
Тогда![]()
Подставляя
найденные выражения в равенство (30),
получим![]() (32)
(32)
Это разложение функции f(x) в ряд называется рядом Маклорена.
