П5. Метод итераций (метод последовательных приближений).

Основным преимуществом этого метода является однотипность выполняемых на каждом шаге операций, что облегчает составление программ для ЭВМ.

Сущность метода состоит в следующем:

Рассмотрим уравнение:

f(x) = 0 (1).

Пусть f(x) – непрерывная на функция, обращающаяся внутри этого интервала в нуль, по крайней мере, один раз. Требуется уточнить хотя бы один из вещественных корней, расположенных на .

Заменим уравнение (1) эквивалентным ему уравнением (2).

Выберем в качестве начального приближения какое-либо значение , например:

.

Затем вычислим и полученное число примем за первое приближение искомого корня . Подставив вместо х в правую часть уравнения (2), получим новое число:

и т.д.

Продолжая этот процесс, приходим к последовательности чисел .

Если и функция непрерывна, то получим, что: , т.е. является корнем уравнения (1).

Функция в уравнении (2) может быть найдена различными способами. Вид функции оказывает большое влияние, как на сам факт сходимости, так и на ее скорость.

Теорема. Пусть выполнены условия:

определена и дифференцируема на ;

все значения при х ;

такое число <1, что при х <1 (3).

Тогда итерационный процесс:

сходится независимо от выбора начального приближения , и есть единственный и однократный корень уравнения на .

Оценка погрешности:

,

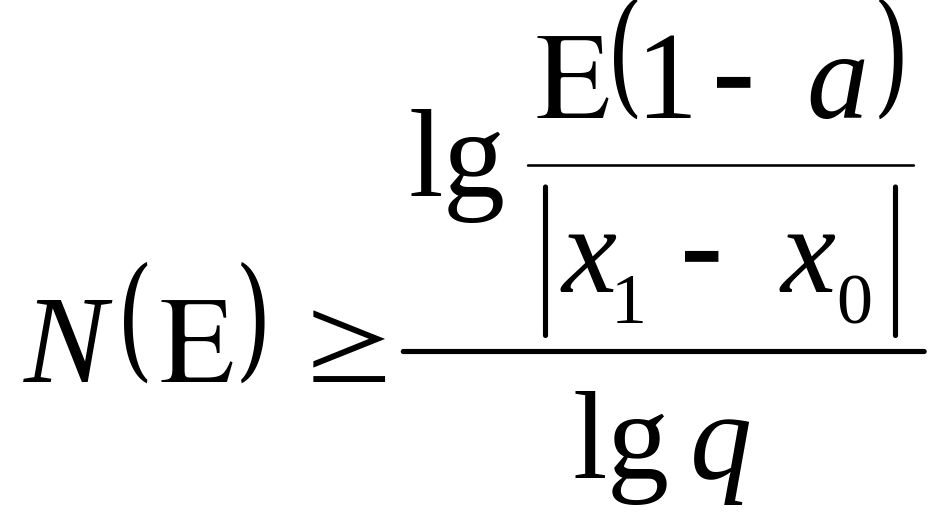, где N(E) – максимальное число итераций, необходимых для вычисления корня с заданной точностью.

При q :

.

Для выбора функции можно пользоваться следующим приемом.

Рассмотрим f(х) = 0 (1).

Пусть , и пусть > 0.

,

,

.

Заменим уравнение (1) следующим уравнением:

и выберем таким образом, чтобы выполнялось условие 3 теоремы:

,

,

< 1,

-1 < 1- <1,

-2 < < 0, > 0,

0 < < , ,

или 0 < < .

Обычно в качестве выбирают . Таким образом, имеем уравнение:

.

Тогда соответствующий итерациональный процесс имеет вид:

.

Аналогично, если < 0, то:

.

Геометрическая интерпретация.

Пример 1: .

,

, f(0) < 3; f(1) = -12.

Данное уравнение приведем к виду .

1) , ;

2) , ;

3) , .

Т.к. q < 1, то:

> 1 на ;

< 1 на .

Следовательно, можно взять :

,

до тех пор, пока:

.

Или: , .

,

< 0,

следовательно:

,

где ,

,

.

Т3. Методы решения системы двух нелинейных уравнений. §1. Постановка задачи.

Пусть дана система двух нелинейных уравнений с двумя неизвестными:

(1),

где и – нелинейные функции, определенные и непрерывные в некоторой области . Требуется найти такой вектор , который при подстановке в систему (1) превращает каждое уравнение в верное числовое равенство.

Замечание. Для рассматриваемых ниже методов требуется находить начальное приближение . Предполагается, что система (1) имеет лишь изолированные корни. Число этих корней и их грубые приближенные значения можно установить, построив кривые и и определив координаты их точек пересечения.