Т6. Численное решение Определенного интеграла. П1. Приближенное вычисление определенного интеграла.

Пусть требуется найти определенный интеграл от непрерывной функции f(x). Если можно найти первообразную F(x) функции f(x), то интеграл вычисляется по формуле Ньютона-Лейбница:

= F(b)-F(a).

Но отыскание первообразной функции иногда весьма сложно; кроме того, как известно, не для всякой непрерывной функции ее первообразная выражается через элементарные функции. В этих и других случаях (например, функция у = f(x) задана графически или таблично) прибегают к приближенным формулам, с помощью которых определенный интеграл находится с любой степенью точности.

Рассмотрим три наиболее употребительные формулы приближенного вычисления определенного интеграла – формулу прямоугольников, формулу трапеций, формулу парабол (Симпсона), основанные на геометрическом смысле определенного интеграла.

П2. Формула Прямоугольников.

П усть на отрезке [a; b], a < b, задана непрерывная функция f(x). Требуется вычислить интеграл , численно равный площади соответствующей криволинейной трапеции. Разобьем основание этой трапеции, т. е. отрезок [a; b], на n равных частей (отрезков) длины h = = = x_i – x_i-1 (шаг разбиения) с помощью точек х₀ = а, x_i, x₂, ... , x_n = b. Можно записать, что x_i = x₀ + h*i, где i = 1,2, ... , n.

В середине c_i = каждого такого отрезка построим ординату =f(c_i) графика функции y=f(x). Приняв эту ординату за высоту, построим прямоуголь­ник с площадью h* .

Тогда сумма площадей всех n прямоугольников дает площадь ступенчатой фигуры, представляющую собой приближенное значение искомого определенного интеграла:

≈ = (1)

формула (1) называется формулой средних прямоугольников.

Абсолютная погрешность приближенного равенства (1) оценивается с помощью следующей формулы:

где M₂ – наибольшее значение |f "(x)| на отрезке [a; b].

Отметим, что для линейной функции (f(x) = kx + b) формула (1) дает точный ответ, поскольку в этом случае f "(x) = 0.

П3. Формула трапеций.

Формулу трапеций получают аналогично формуле прямоугольников: на каждом частичном отрезке криволинейная трапеция заменяется обычной.

Р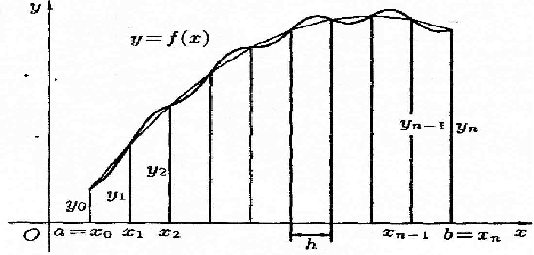 азобьем отрезок [a; b] на n равных частей длины h = .Абсциссы точек деления а = x₀, x₁, x₂, … , b = x_n. Пусть y₀, y₁, … , y_n – соответствующие им ординаты графика функции. Тогда расчетные формулы для этих значений примут вид x_i = a + h*i, y_i­=f(x_i), i = 0, 1, 2, … ,n; h = :

Заменим кривую у = f(x) ломаной линией, звенья которой соединяют концы ординат y_i и y_i+i (i = 0, 1, 2, ... , n). Тогда площадь криволинейной трапеции приближенно равна сумме площадей обычных трапеций с основаниями y_i, y_i+1 и высотой h =

≈

или

≈ (1)

формула называется формулой трапеций.

Абсолютная погрешность Rn приближения, полученного по формуле трапеций, оценивается с помощью формулы где M₂ = max |f"(x)|. Снова для линейной функции у = kx + b формула (1) – точная.

П4. Формула парабол (Симпсона)

Если заменить график функции у = f(x) на каждом отрезке [x_i-1, x_i] разбиения не отрезками прямых, как в методах трапеций и прямоугольников, а дугами парабол, то получим более точную формулу приближенного вычисления интеграла .

Предварительно найдем площадь S криволинейной трапеции, ограниченной сверху графиком параболы у — ах² + bx + с, сбоку – прямыми x = - h, х = h и снизу – отрезком [–h; h].

П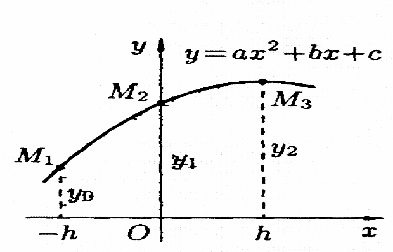 усть парабола проходит через три точки М₁(–h;y₀), М₂(0, y₁), M₃(h; у₂), где у_о = ah² – bh + c – ордината пара­болы в точке х = –h; у₁ = с – ордината параболы в точке x = 0; y₂ = ah² + bh+c – ордината параболы в точке x – h. Площадь S равна

(1)

Выразим эту площадь через h, у_о, у₁, у₂. Из равенств для ординат у₂ находим, что с = у₁ а = (y₀+2y₁+y₂). Подставляя эти значения c и а в равенство (1), получаем:

(2)

Получим теперь формулу парабол для вычисления интеграла .

Для этого отрезок [а; b] разобьем на 2п равных частей (отрезков) длиной h = , точками х₂ = x₀ + ih (i = 0, 1, 2, ... , 2n). В точках деления а = х_о, х₁, x₂, ... , x_2n-2, Х_2n-1, Х_2n = b вычисляем значения подынтегральной функции f(x): у_о, у₁, у₂, … , у_2n-2, У_2n-1, У_2n, где у₂ = f(х₁).

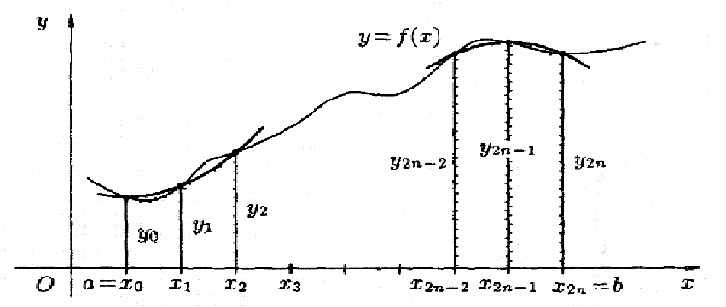
Заменяем каждую пару соседних элементарных криволинейных трапеций с основаниями, равными h, одной элементарной параболической трапецией с основанием, равным 2h. На отрезке [х_о; x₂] парабола проходит через три точки (хо; y₀), (x₁; y₁), (х₂; y₂) – Используя формулу (2), находим:

Аналогично находим:

, … ,

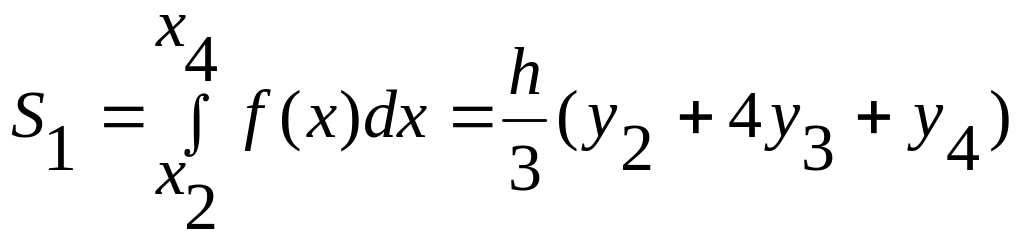Сложив полученные равенства, имеем:

≈ (y₀+4y₁+2y₂+ … +2y_2n-2+4y_2n-1+y_2n)

Или

≈ ((y₀+y_2n)+4(y­­­­₁+y₃+ … +y_2n-1)+2(y₂+y₄+ … +y_2n-2)) (3)

Формула (3) называется формулой парабол (или Симпсона).

Абсолютная погрешность вычисления по формуле (3) оценивается соотношением:

, где: M₄= |f^iv(x)|

О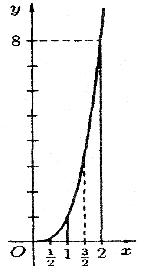 тметим, что формула (3) дает точное значение интеграла во всех случаях, когда f(x) – многочлен, степень которого меньше или равна трем (тогда f ^iv = 0).

Пример: Вычислить , разбив отрезок интегрирования [0; 2] на 4 части.

Решение: Имеем: f(x) = х³,

a=x₀=0; b=x₄=2; h= = = ,

x₀=0, y₀=0; x₁= , y₁= ; x₂=1, y₂=1;

x₃= , y₃= ; x₄=2, y₄=8;

а) по формуле прямоугольников:

с₁= , = ; c₂= , = ;

c₃= , = ; c₄= , = ,

≈ ( + + + )=3,875, т.е. ≈3,875;

б) по формуле трапеций:

≈ ( )=4,25, т.е. ≈4,25;

в) по формуле парабол:

≈ =4, т.е. ≈4.

Точное значение интеграла =

Абсолютные погрешности соответствующих формул таковы: а) 0,125; б) 0,25; в) 0.

81