П.3. Метод Ньютона (метод касательных).

Пусть уравнение f(x) = 0 имеет корень , причем и непрерывны и сохраняют постоянные знаки на .

Геометрический смысл метода Ньютона состоит в том, что дуга кривой у = f(x) заменяется касательной к этой кривой.

Первый случай. > 0

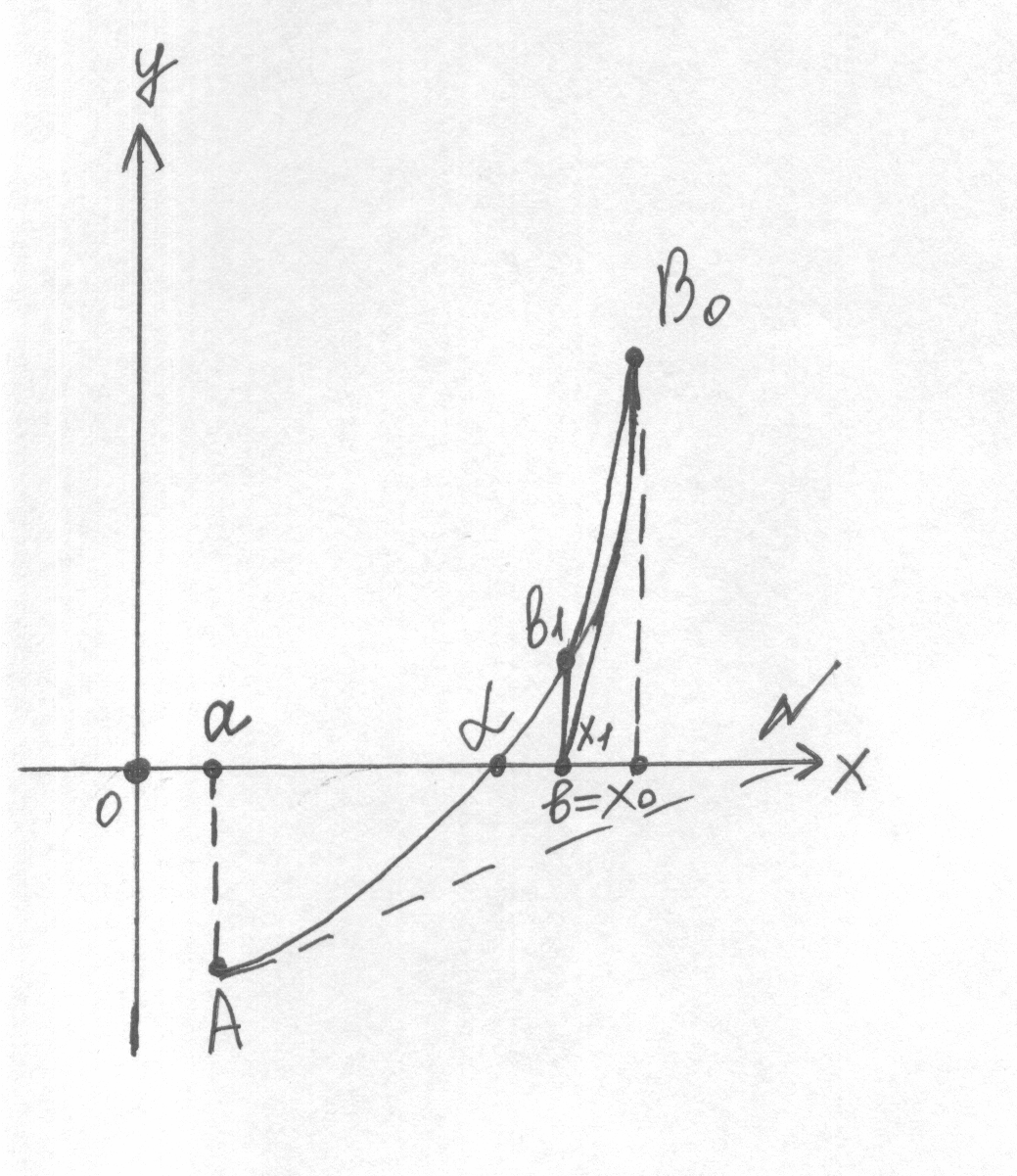
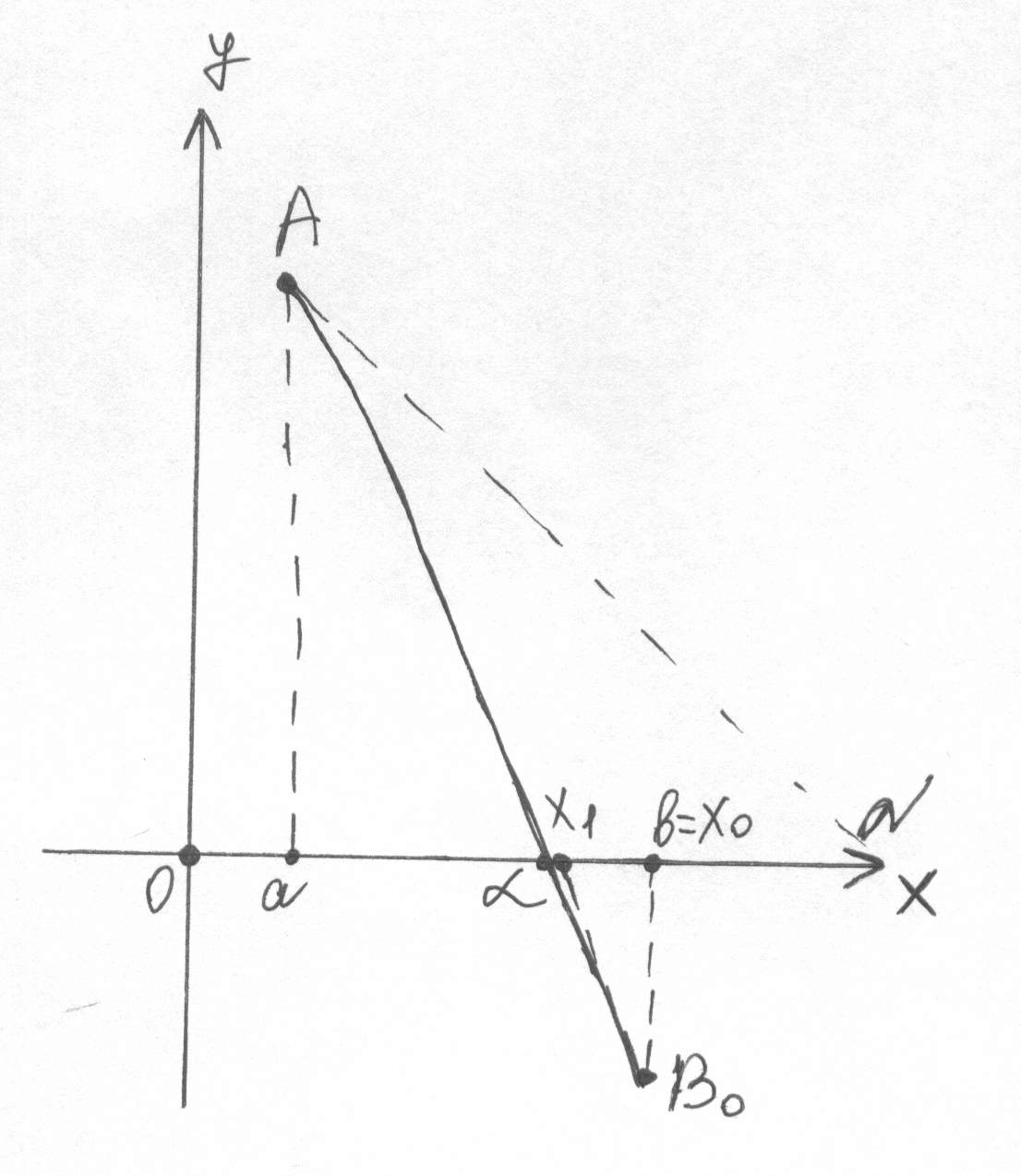
f(x) возрастает и вогнута, f(x) убывает и выпукла,

f(а) < 0, f(b) > 0. f(а) > 0, f(b) < 0.

Проведем касательную к кривой у = f(x) в точке и найдем абсциссу точки пересечения касательной с осью ох.

.

При у = 0 найдем – точку пересечения с осью ох.

,

.

Теперь корень уравнения . Применяя снова метод Ньютона, проведем касательную к кривой в точке .

Получим:

и т.д.

.

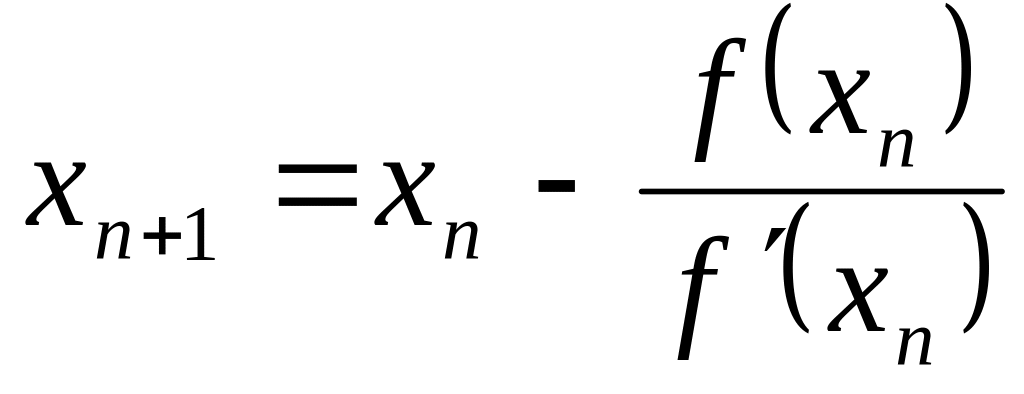Получаем последовательность , , …, , … . Каждый последующий член ближе к точному корню , чем предыдущий.

Однако все > , т.е. – приближенное значение корня с избытком.

Второй случай. < 0.

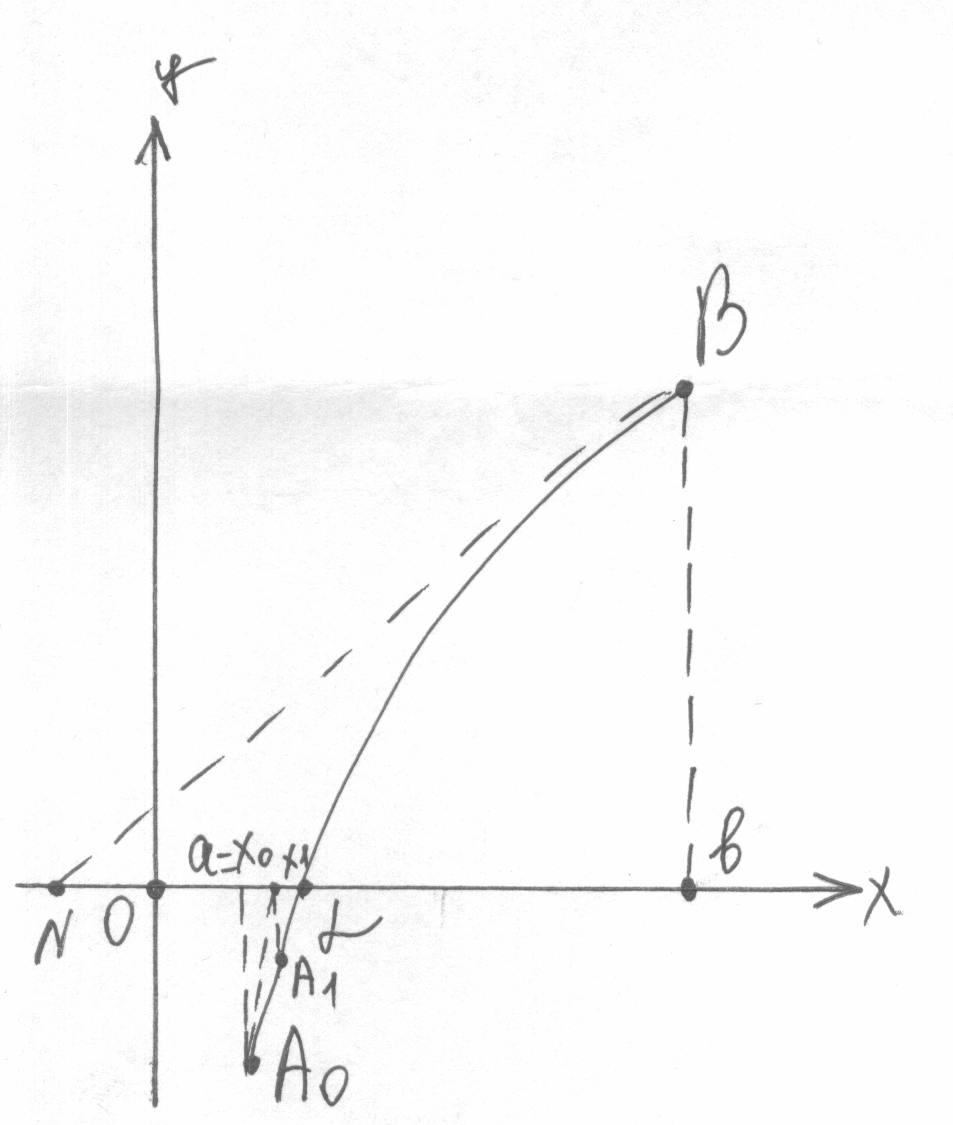
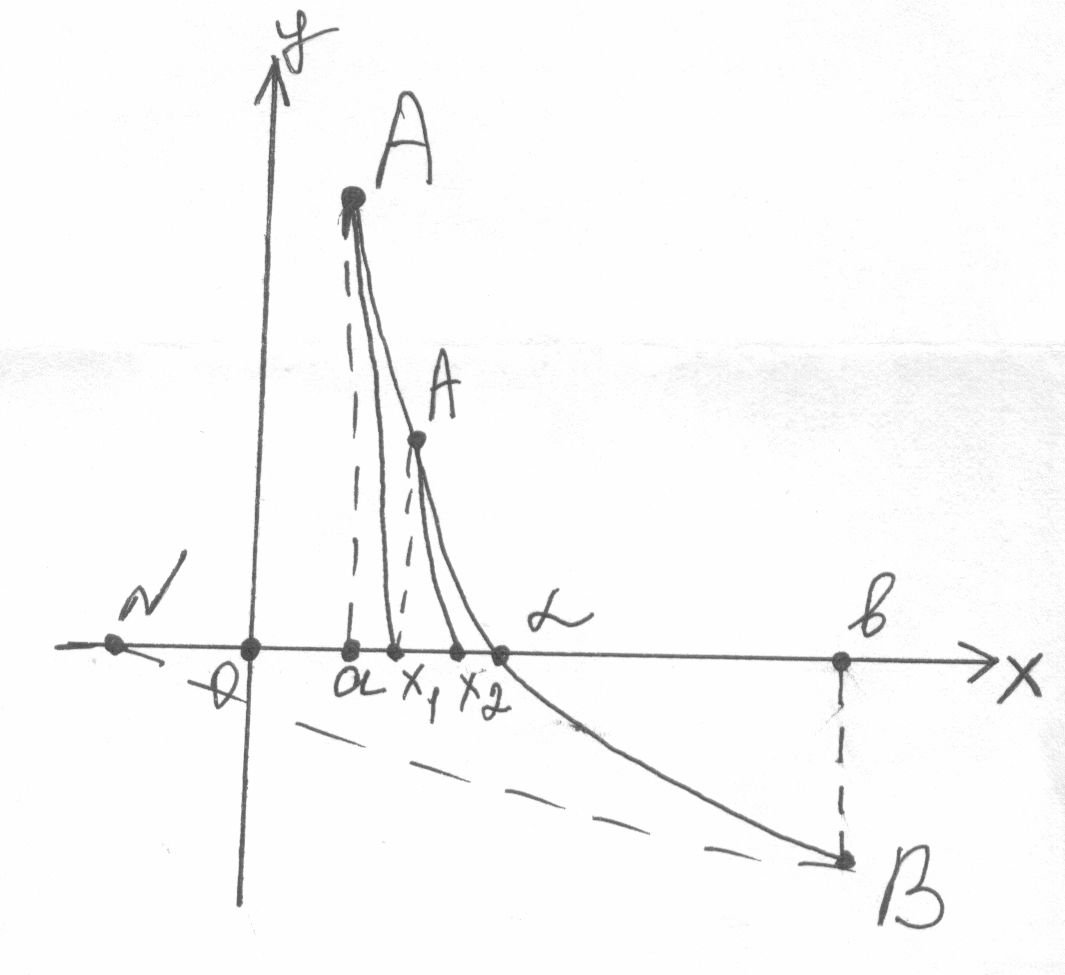
f(x) возрастает и выпукла, f(x) убывает и вогнута,

f(a) < 0, f(a) > 0. f(a) > 0, f(b) < 0.

Касательная в точке B пересечет ось ох в точке .

Поэтому проведем касательную в точке и запишем ее уравнение:

.

Полагая, что у = 0, :

;

.

Применяя снова метод Ньютона, проведем касательную в точке и получим:

и т.д.

.

Правило. При выборе начального приближения корня за исходную точку следует выбрать тот конец , в котором знак функции совпадает со знаком .

В первом случае:

f(b) · > 0 и начальная точка .

Во втором случае:

f(а) · > 0 и начальная точка .

Для оценки погрешности можно пользоваться общей формулой:

,

где .

Эта формула годится и для метода хорд.

З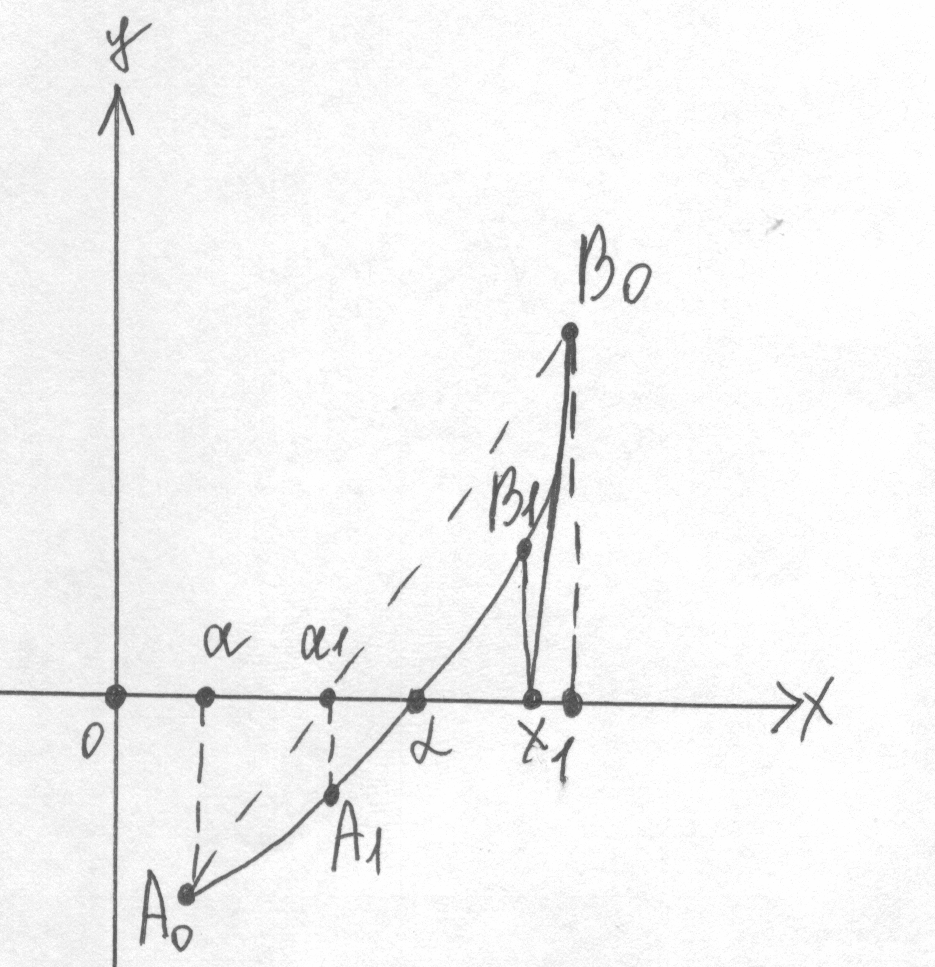 амечание. Если производная мало изменяется на , то для упрощения вычислений можно пользоваться формулой:

,

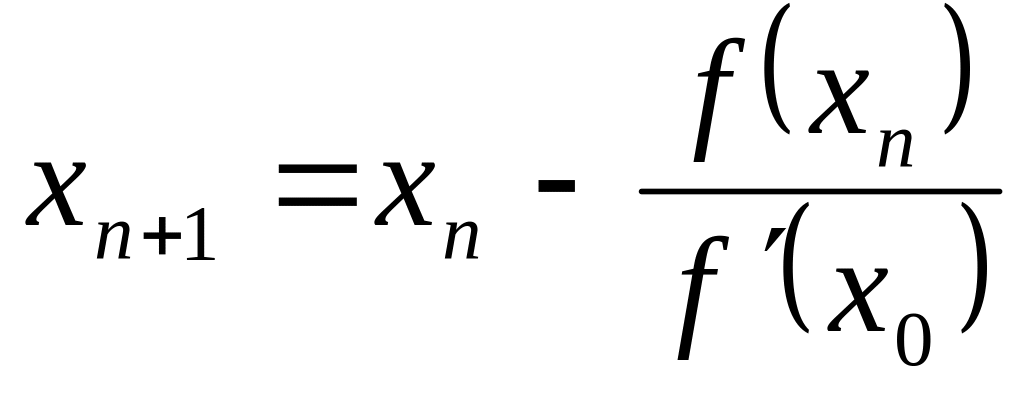т.е. значение производной в начальной точке достаточно вычислить только один раз.

Геометрически это означает, что касательная в точках заменяются прямыми, параллельными касательной, проведенной в точке .

П4. Методы хорд и касательных.

Методы хорд и касательных дают приближения корня с разных сторон. Поэтому их часто применяют в сочетании друг с другом, и уточнение корня происходит быстрее.

Пусть дано уравнение f(х) = 0, корень отделен и принадлежит .

Если > 0, то метод хорд дает приближения корня с недостатком, а метод касательных – с избытком.

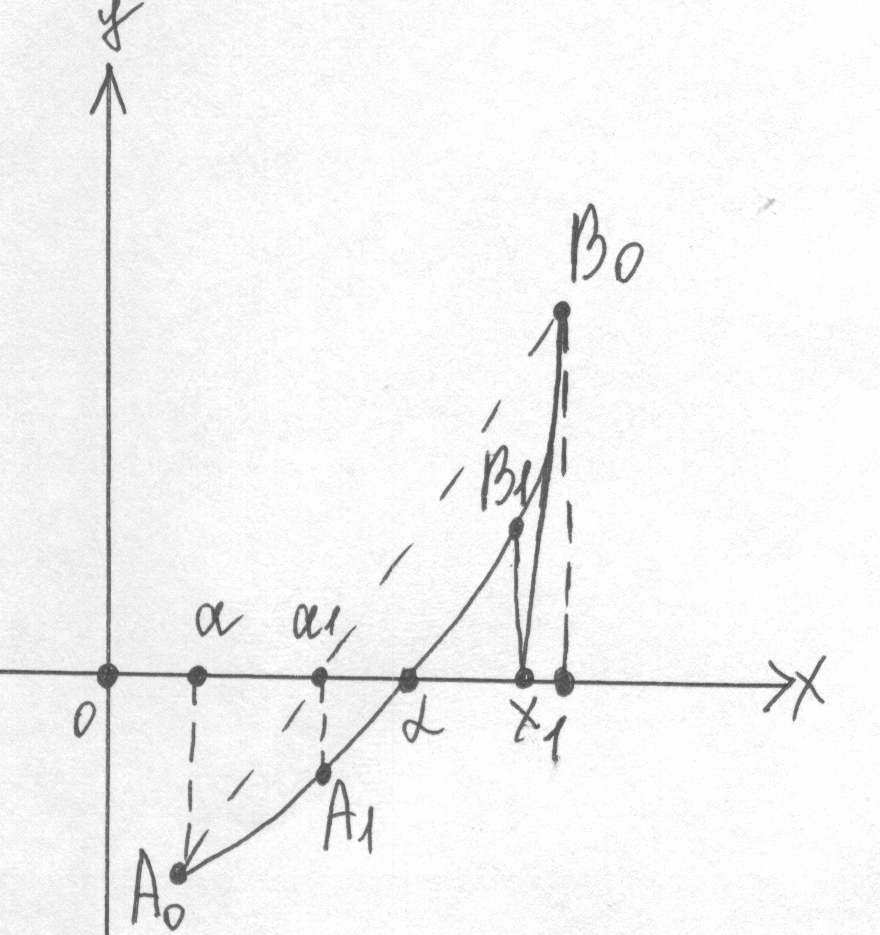
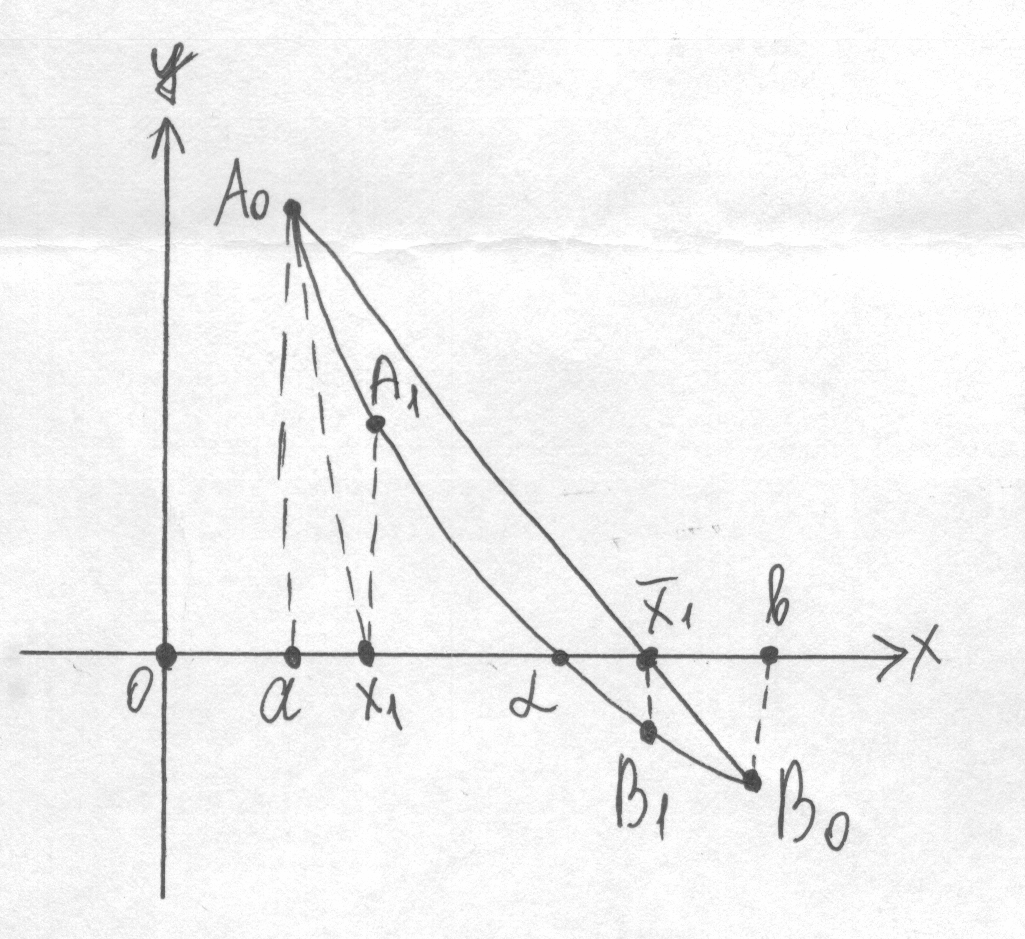
В этом случае для метода хорд следует взять конец а, для метода касательных – b, тогда:

,

.

Теперь . Применяя к этому отрезку комбинированный метод, получаем:

,

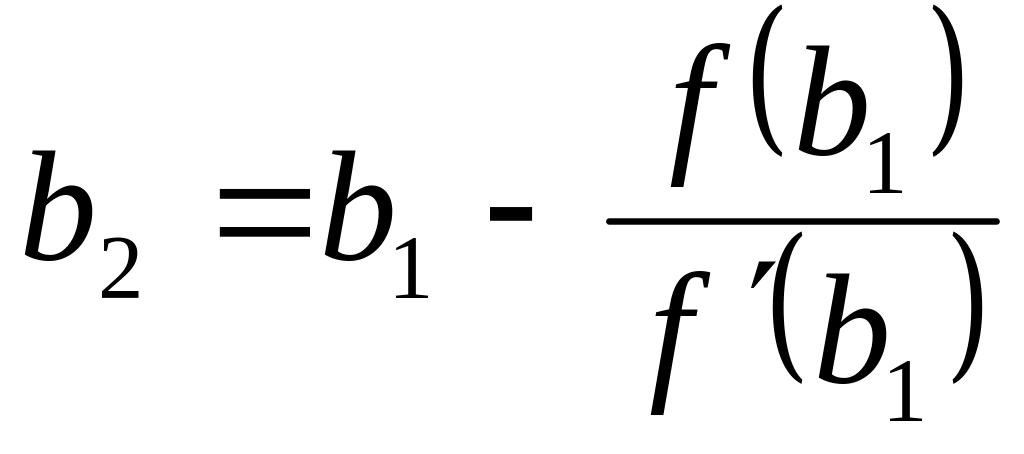и т.д.

;

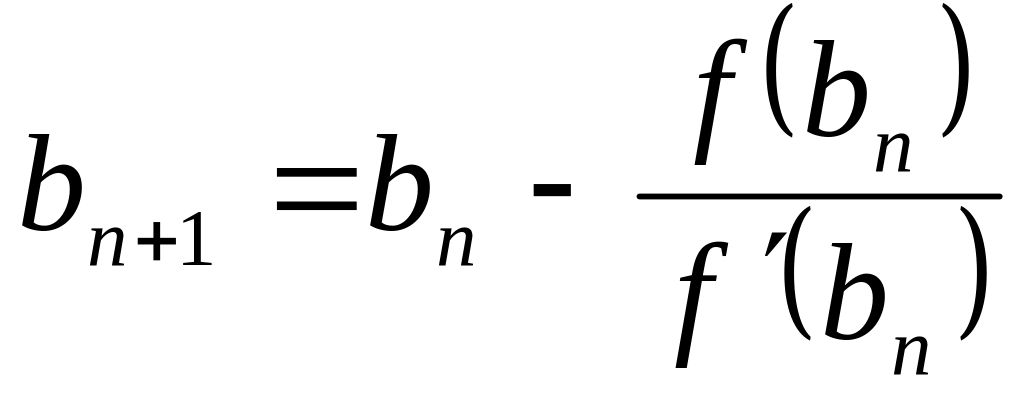(2).

Если же < 0, то методом хорд получаем значение корня с избытком, а методом касательных – с недостатком.

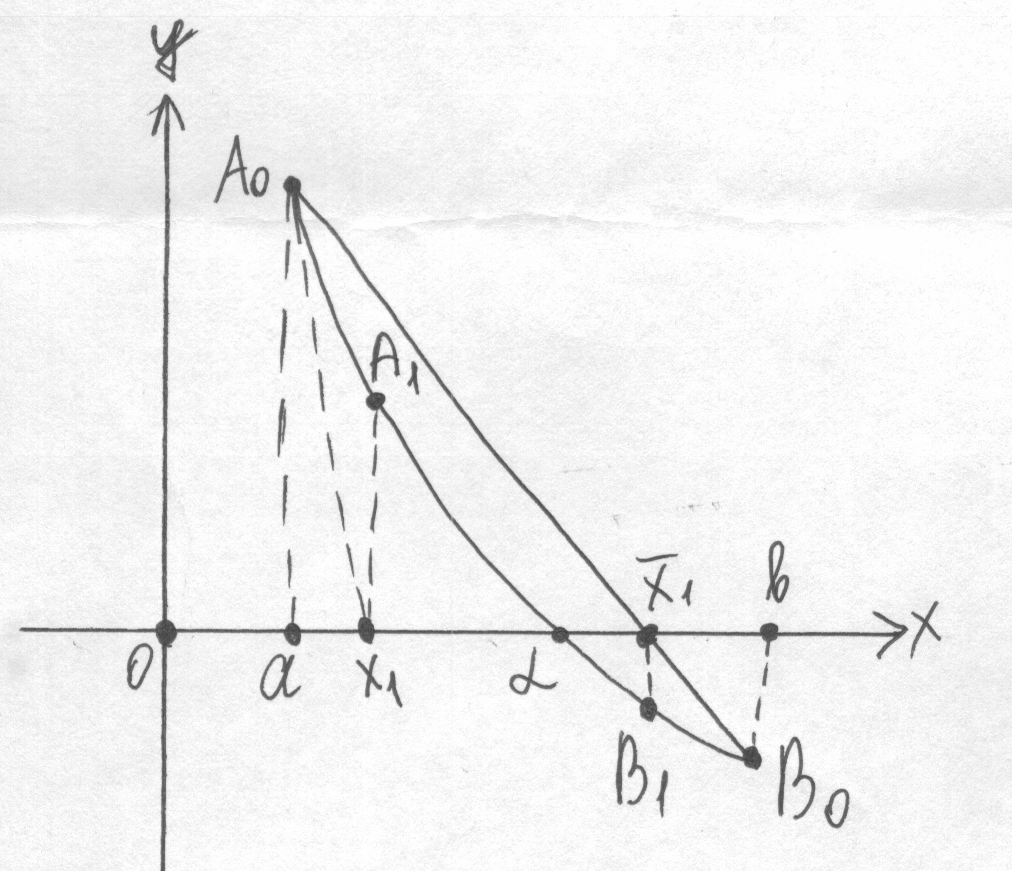
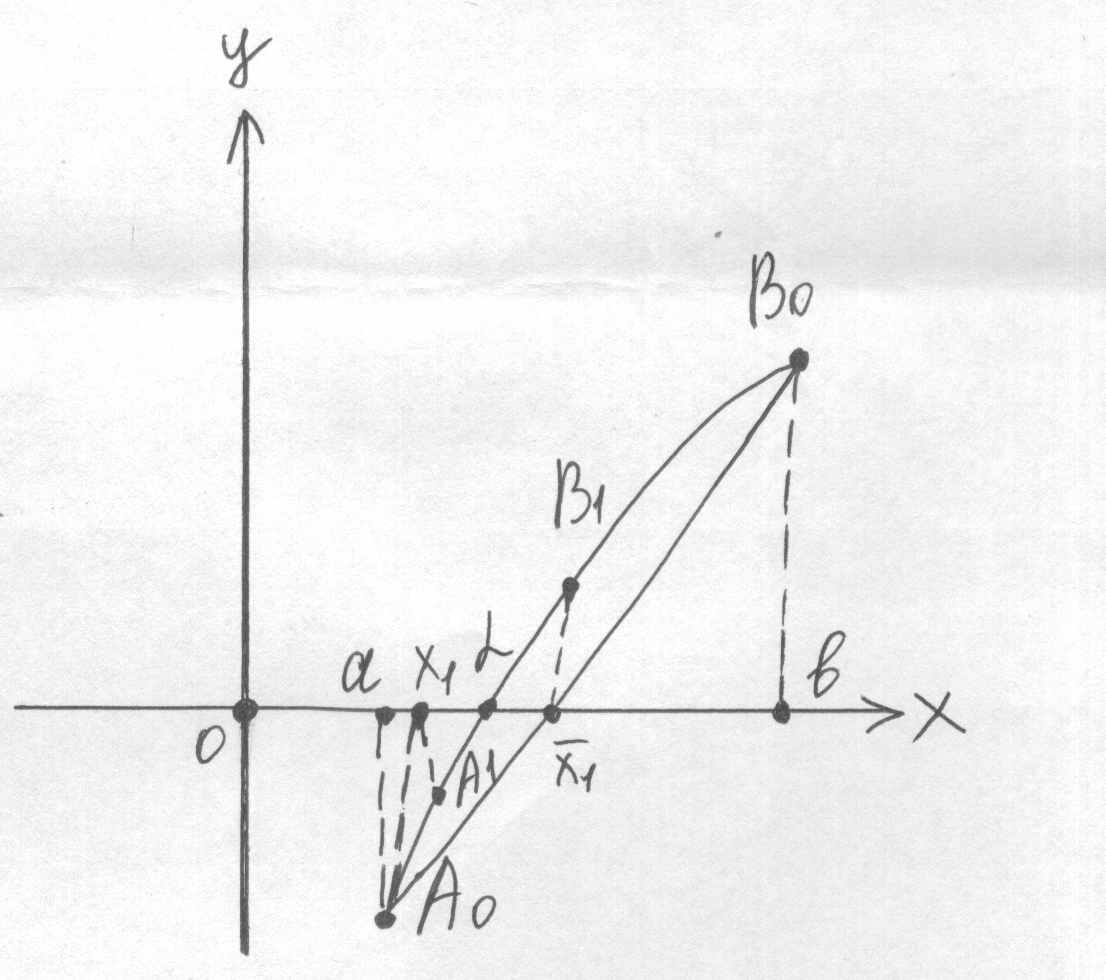
В этом случае конец а берется для метода касательных, а b – для метода хорд. Тогда:

,