§3. Графическое решение уравнений.

Действительные корни уравнения

f (x) = 0 (1)

приближенно можно определить как абсциссы точек пересечения графика функции y = f(х) с осью ох.

На практике часто бывает выгодно уравнение (1) заменить равносильным ему уравнением:

( ) = ( ) (2),

где функции ( ) и ( ) более простые, чем функция f(х).

Тогда искомые корни получим как абсциссы точек пересечения этих графиков.

Например:

lg – 1 = 0, lg = ,

D(f) : > 0, ,

( ) = , lg 2 0,3, lg 3 0,48,

.

Нахождение корней упрощается, если одна из функций ( ) или ( ) линейная.

Например, в уравнениях х + ax + b = 0.

Графические методы решения уравнений весьма удобны и сравнительно просты, но они применяются лишь для грубого определения корней. Далее корни уточняют каким-либо способом.

§4. Уточнения корня уравнения.

Пусть дано уравнение:

f (x) = 0 (1)

и отделен простой корень ,

т.е. f(a) · f(b) < 0.

Отрезок называется начальным отрезком неопределенности. Уточнение корня заключается в построении последовательности вложенных друг в друга отрезков , каждый из которых содержит уравнения.

Если с , то в качестве может быть выбран тот из отрезков или , который содержит искомый корень .

В зависимости от способа выбора такой точки с мы получим различные методы уточнения корня.

П1. Метод половинного деления.

Этот метод состоит в следующем:

Делим отрезок пополам:

с = .

Проверяя знаки f(a), f(c), f(b) выясняем, какой половине принадлежит корень. Полученную половину снова делим пополам и т.д. до тех пор, пока не выполнится условие:

< ,

где n – число проведенных делений. После этого любую из границ последнего отрезка можно взять в качестве .

Замечание. Этот метод является сходящимся, т.е. за каждую операцию погрешность уменьшается в 2 раза. Для достижения искомой погрешности необходимо выполнить:

n = log операций.

Например, если:

b – a = 1, a · = 10 , то:

.

Недостаток метода в том, что не может использоваться для нахождения корней четной степени (f(a) · f(b) 0).

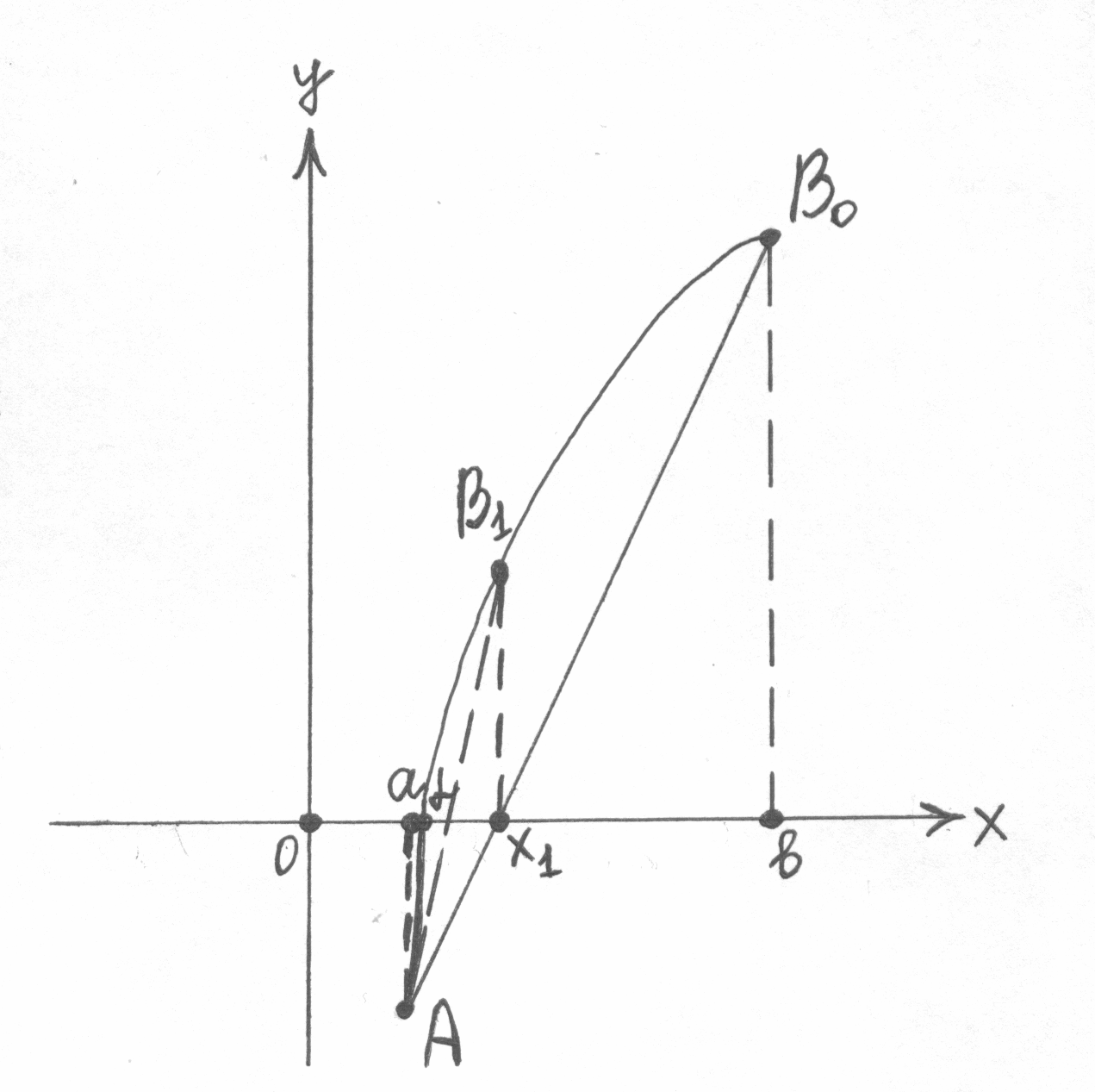
П.2. Метод хорд.

Пусть дано уравнение f(x) = 0, где f(x) – непрерывная функция, имеющая на (a; b) производные 1-ого и 2-ого порядка. Корень считается отделенным и находится на отрезке , т.е.:

f(a) · f(b) < 0.

Идея метода состоит в том, что на достаточно малом промежутке дуга кривой y = f(x) заменяется стягивающей ее хордой. В качестве приближенного значения корня принимается точка пересечения хорды с осью ох.

Первый случай. > 0.

f(x) возрастает и вогнута, f(x) убывает и выпукла,

f(а) < 0, f(b) > 0. f(а) > 0, f(b) < 0.

Уравнение хорды, проходящей через точки A , B, имеет вид:

.

Найдем значение х = х , для которого у = 0.

,

.

Теперь точный корень .

Если точность корня нас не устраивает, то применим метод хорд к отрезку .

.

Затем применяем этот метод к отрезку ; находим:

и т.д.

(1).

Процесс продолжаем до тех пор, пока не получим приближенный корень с заданной степенью точности.

Второй случай. < 0.

f(x) убывает и вогнута, f(x) возрастает и выпукла,

f(a) > 0, f(b) < 0. f(a) < 0, f(a) > 0.

Уравнение хорды АВ имеет вид:

.

При у=0:

,

.

и т.д.

(2).

Итак, если > 0, то находится по формуле (1), а если < 0, то находится по формуле (2).

Однако, выбор формулы можно осуществить, пользуясь простым правилом.

Правило. Неподвижным концом отрезка является тот, для которого знак функции совпадает со знаком второй производной.

При оценке погрешности приближения можно пользоваться формулой:

< .