
- •Т1. Элементарная теория погрешностей. §1. Источники и классификация погрешностей.
- •§2. Точные и приближенные числа. П1. Десятичная запись и округление чисел.
- •П2. Абсолютная и относительная погрешности.
- •П3. Верные значащие цифры. Связь между числом верных знаков и погрешностью числа.
- •П4. Погрешности вычислений с приближенными данными.
- •Т2. Методы решения нелинейных уравнений. §1. Постановка задачи.
- •§2. Отделение корней уравнения.
- •§3. Графическое решение уравнений.
- •§4. Уточнения корня уравнения.
- •П1. Метод половинного деления.
- •П.2. Метод хорд.
- •П.3. Метод Ньютона (метод касательных).
- •П4. Методы хорд и касательных.
- •П5. Метод итераций (метод последовательных приближений).
- •Т3. Методы решения системы двух нелинейных уравнений. §1. Постановка задачи.
- •§2. Метод итераций.
- •§3. Метод Зейделя.
- •§4. Метод Ньютона.
- •Т4. Численные методы решения задач линейной алгебры. §1. Методы решения систем линейных алгебраических уравнений (слау). П1. Постановка задачи.
- •П2. Метод Гаусса (метод исключения неизвестных).
- •П3. Метод итераций (метод последовательных приближений).
- •П4. Метод Зейделя.
- •П5. Метод прогонки решения систем с трехдиагональными матрицами коэффициентов.
- •Т5. Интерполирование функций. §1. Постановка задачи.
- •§2. Интерполяционный многочлен Лагранжа.
- •§3. Интерполяционные многочлены Ньютона.
- •П1. Конечные разности.
- •П2. Первая интерполяционная формула Ньютона.
- •П3. Вторая интерполяционная формула Ньютона.
- •П4. Погрешность интерполяционных процессов.
- •§4. Метод наименьших квадратов. П1. Постановка задачи.
- •П2. Критерий согласия.
- •Т6. Численное решение Определенного интеграла. П1. Приближенное вычисление определенного интеграла.
- •П2. Формула Прямоугольников.
- •П3. Формула трапеций.
- •П4. Формула парабол (Симпсона)
Т1. Элементарная теория погрешностей. §1. Источники и классификация погрешностей.
Погрешность решения задачи обуславливается следующими причинами:
1. Математическое описание задачи является не точным (неустранимая погрешность).
2. Применяемый метод часто не является точным (погрешность метода).
3. При выполнении арифметических операций производятся округления (вычислительной погрешностью).
Полная погрешность, естественно, равна сумме этих трех погрешностей, т.е.
Рn = Рн + Рм + Рв
§2. Точные и приближенные числа. П1. Десятичная запись и округление чисел.
Всякое десятичное положительное число а может быть представлено в виде конечной или бесконечной десятичной дроби:
а = α1 * 10m + α2 * 10m-1 + … + αn * 10m-n+1 + … (1)
где: αn – цифры числа n=1,2,… , причем α1 ≠ 0, а m – старший десятичный разряд числа а.
Каждая единица соответствующего n-го разряда, если считать слева на право, имеет свое значение 10m-n+1 называемое ценой разряда. Так цена первого (слева) разряда 10m, второго – 10m-1 и т.д
На практике часто возникает необходимость в округлении числа, т.е. в замене его другим числом с меньшим количеством цифр.
Правила округления:
1. Если отбрасываемые цифры составляют число, большее половины единицы последнего оставляемого разряда, то последняя оставляемая цифра усиливается (увеличивается на единицу). Если же меньше, то оставляемые цифры не изменяются.
2. Если отбрасываемые цифры составляют число, равное половине единицы последнего оставляемого разряда, то последняя цифра усиливается, если она нечетная и остается без изменения, если она четная (правило четной цифры).
![]()
П2. Абсолютная и относительная погрешности.
Пусть А – точное число, а а - его приближенное значение. Если а<А, то а – приближенное значение по недостатку, а если а >А, то – по избытку.
Разность А - а называется ошибкой или погрешностью.
Абсолютной погрешностью приближенного числа а называется величина Δа ≥ /A – a /
Абсолютная погрешность представляет собой верхнюю границу отклонения точного числа А от приближенного:
А = а ± Δа (3)
В качестве абсолютной погрешности берут по возможности наименьшее число.
Абсолютная погрешность отражает лишь количественную сторону погрешности, но не качественную, т.е. не показывает хорошо или плохо произведено измерение или вычисление.
Для оценки качества вычислений вводится понятие относительной погрешности.
Определение:
Относительной погрешностью приближенного числа а называется величина δа, удовлетворяющая неравенству:
δа
≥
![]() ,
а ≠ 0 (4) или δа
≥
,
а ≠ 0 (4) или δа
≥
![]() ,
а
≠ 0
(5)
,
а
≠ 0
(5)
Учитывая (3) можно записать:
А = а (1 ± δа) (6)
Относительная погрешность есть отвлеченное число и ее иногда выражают в %.
П3. Верные значащие цифры. Связь между числом верных знаков и погрешностью числа.
Определение:
Значащими цифрами числа называются все его цифры, кроме нулей, стоящих левее первой отличной от нуля цифры.
Нули в конце числа всегда значащие цифры (в противном случае их не пишут).
0,001604 – 4 значащие цифры;
30,500 – 5 значащих цифр.
Если мы хотим показать, что у числа 400000 последние 3 нуля не являются значащими, то данное число надо записать в виде двух сомножителей:
400·10![]() ,
или 40,0·10
,
или 40,0·10![]() ,
или 0,400·10
,
или 0,400·10![]() .
.
Последняя запись называется нормализованной и является предпочтительной. В этом случае говорят, что 400 есть мантисса, а 6 – его порядок. Если число записано в виде
![]() =
=
![]() ·10
·10![]() <
<![]() ·10
·10![]() +…+
+…+
![]() ·10
·10![]() +…,
+…,
то цифра αn называется верной значащей цифрой или просто верной, если выполняется неравенство:
![]()
![]() 0,5·10
(1),
0,5·10
(1),
т.е. если абсолютная величина разности между точным числом и его приближенным не превосходит половины единицы десятичного разряда, в котором стоит αn.
Т.к. Δа,
то неравенство (1) заменяется неравенством:
Δа 0,5·10 (2).
С другой стороны, если задано число n верных знаков приближенного числа а, то за абсолютную погрешность можно принять:
Δа= 0,5·10 (3).
Если неравенство (2) не выполняется, то цифра αn называется сомнительной.
Если цифра αn - верная, то и все предыдущие верные.
Разделив
обе части неравенства (1) на
![]() ,
получим:
,
получим:
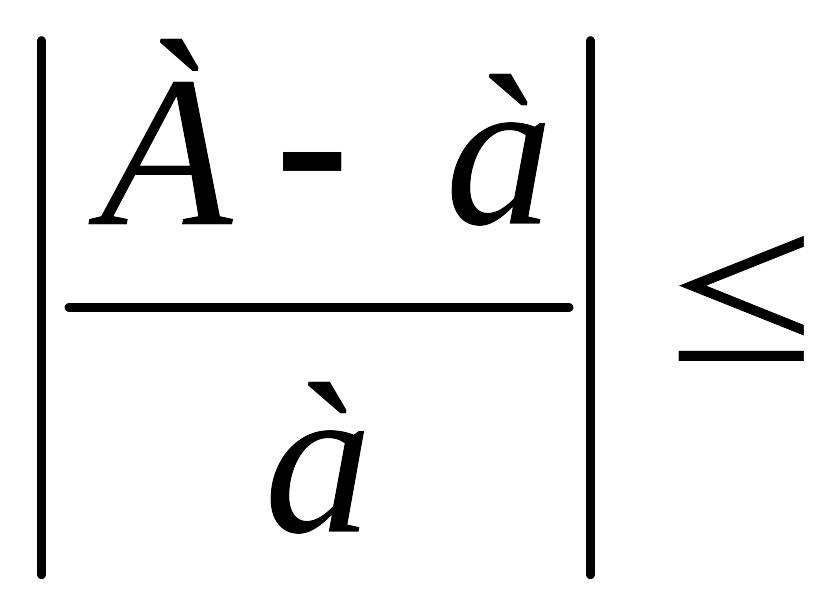
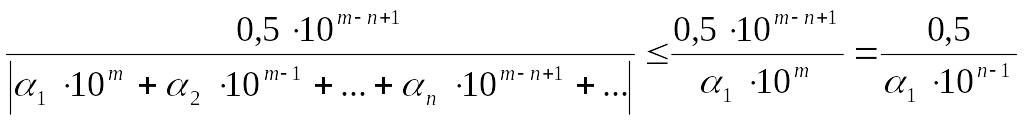
Т.е., если αn - верная цифра, то:
![]() (5).
(5).
С другой стороны, чтобы цифра αn была верной, необходимо, чтобы выполнялось неравенство:
![]() (6),
(6),
т.к. в этом случае выполняются неравенства (1) и (4).
