1.4. Непосредственное интегрирование.

Интегрирование, основанное на применении табличных интегралов, основных свойств неопределенного интеграла, а также простейших тождественных преобразований подынтегральной функции, принято называть, непосредственным интегрированием.

Пример. Найти интеграл:

Решение

Предварительно преобразуем подынтегральную функцию, затем применим свойства неопределенного интеграла и табличный интеграл (1).

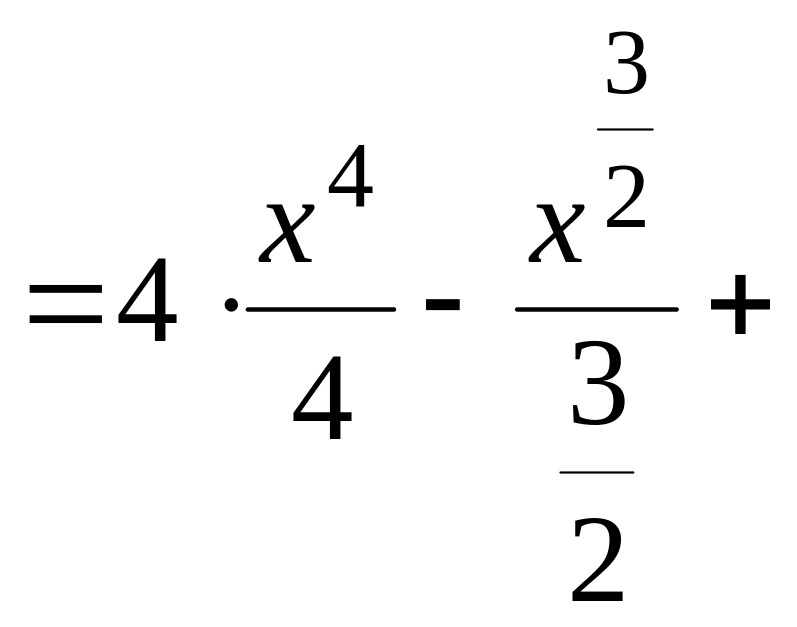
Замечание. При сведении данного интеграла к табличному часто используются следующие преобразования дифференциала, называемые операцией «подведения под дифференциал»: du = d (u ± а), а − число

, k0 − число

udu = d (u²),

соs u du = d(sin u),

sin u du = − d (cos u)

,

В общем случае,

Примеры.

1) , по формуле (2) .

2) , по формуле (1).

1.5. Интегрирование заменой переменной (метод подстановки).

Если данный интеграл не является табличным и не может быть найден способом непосредственного интегрирования, то во многих случаях введение новой переменной интегрирования позволяет свести данный интеграл к табличному. В этом сущность метода подстановки.

Часто интеграл можно упростить путем введения новой переменной t. Положим, что x=(t), где (t) − есть монотонная и непрерывно дифференцируемая функция на некотором промежутке. Если на указанном промежутке изменения переменной x функция f(x) интегрируема, то имеет место следующая формула:

= (1.5.1)

После того, как интеграл найден, следует возвратиться к первоначально заданной переменной х.

Иногда вместо подстановки x=(t) применяют подстановку t=(x), тогда . Это означает, что формулу (1.5.1) можно применять справа налево.

Пример. Применяя метод подстановки, найти интеграл .

Решение

Положим t=х²+1, тогда dt=2xdx и xdx= . Получаем

1.6. Интегрирование по частям.

Пусть u=u(x) и v=v(x) − дифференцируемые функции по переменной x. Определим дифференциал произведения этих функций.

d(uv) = udv + vdu, откуда udv = d(uv) − vdu

Проинтегрировав обе части последнего равенства, получим:

= uv − (1.6.1.)

Формула (1.6.1) называется формулой интегрирования по частям. Этой формулой пользуются в тех случаях, когда интеграл есть более простой по сравнению с интегралом . Иногда формулу интегрирования по частям нужно применять несколько раз.

При использовании формулы (1.6.1) очень важно правильно выбрать множители u и dv. Для разложения подынтегрального выражения на указанные множители общих правил нет. Однако существуют некоторые частные указания.

Указание 1. Если подынтегральное выражение есть произведение показательной или тригонометрической функции на многочлен, то за множитель и следует принять многочлен, а за dv обозначить все остальные сомножители.

Указание 2. Если подынтегральное выражение есть произведение логарифмической или обратной тригонометрической функции на многочлен, то за множитель и следует принять логарифмическую или обратную тригонометрическую функцию.

Пример. Найти интеграл .

Решение

Используем указание 1. Пусть u = х и dv = e^x dx, тогда

du = dx, v = = e^x dx.

По формуле (1.6.1) получаем:

= =

Указание 3. В некоторых случаях повторное применение формулы интегрирования по частям приводит к уравнению относительно искомого интеграла. К таким интегралам относятся интегралы вида:

, , , , , и другие.