§22. Несобственные интегралы.

Вычислить несобственные интегралы или установить их расходимость:

Несобственные интегралы 1-го рода:

; ; ; ; .

Несобственные интегралы 2-го рода:

; ; ; ;

; ; ; ;

; ; ; .

§23 Двойной интеграл.

Вычислить двойной интеграл:

; ; ;

; .

6) Вычислить двойной интеграл , если область D есть прямоугольник, стороны которого определены уравнениями и .

7) Вычислить двойной интеграл , если прямоугольная область D ограничена осями координат и прямыми

8) Вычислить двойной интеграл , если область D ограничена осями координат и прямыми .

Вычислить интегралы:

9) ; 10) ; ;

; ; .

15) Вычислить двойной интеграл , если область D есть треугольник с вершинами

16) Вычислить двойной интеграл , если область D есть треугольник с вершинами

Изобразить область D и свести двойной интеграл к повторным, если

17) 18)

19) 20)

Изменить порядок интегрирования в повторных интегралах:

21) 22) ;

.

Пусть заданы область D и функция , определенная в этой области. Начертить область D и вычислить , если:

25) 26)

Вычислить площадь области D, ограниченной линиями:

§24, §25. Криволинейные интегралы.

Вычислить криволинейные интегралы 1-го рода:

где L-отрезок прямой от до .

если AB-дуга полукубической параболы от до .

где L – часть эллипса первой координатной четверти.

где L – контур окружности .

Вычислить криволинейные интегралы 2-го рода:

5) если L – контур, ограниченный параболами и пробегаемый против хода часовой стрелки.

6) по ломаной OAB, если .

L – дуга параболы , пробегаемая от точки до точки .

, где дуга AB есть верхняя половина эллипса .

, если .

где L−дуга первой арки циклоиды .
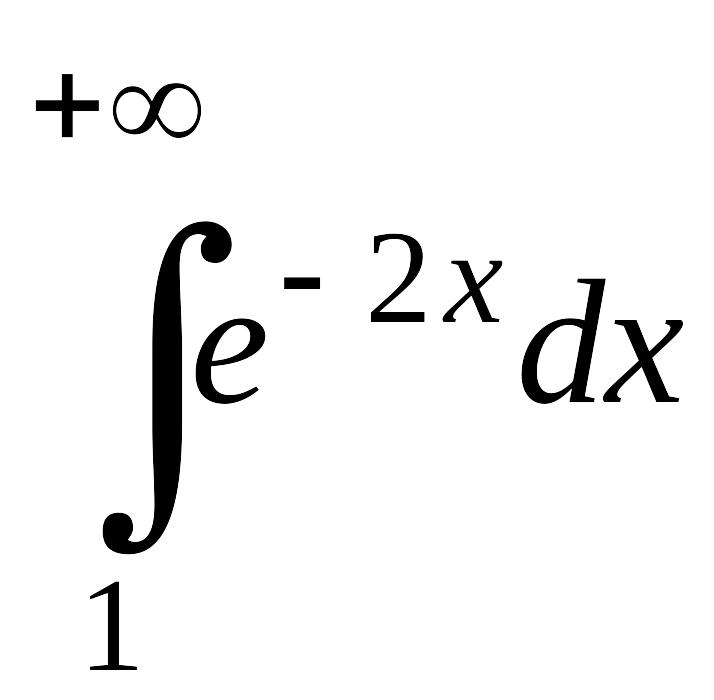
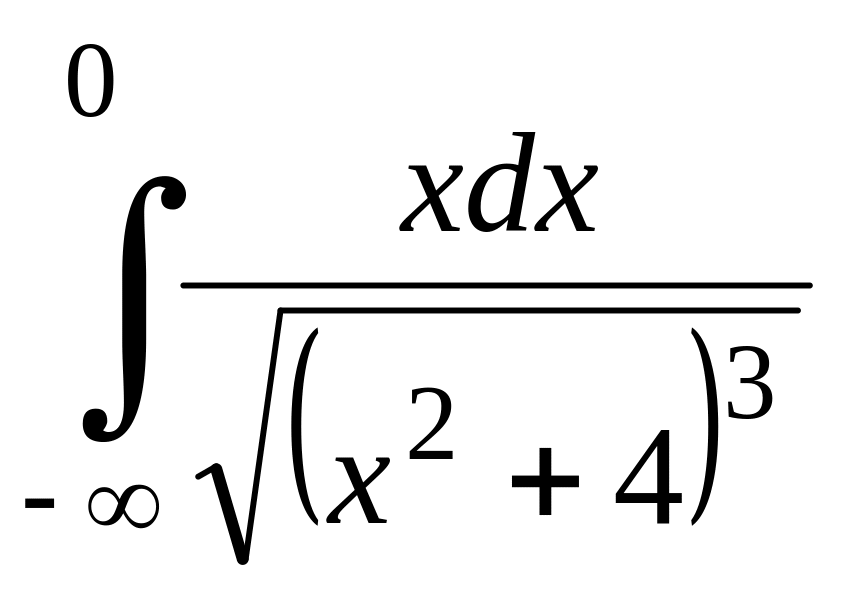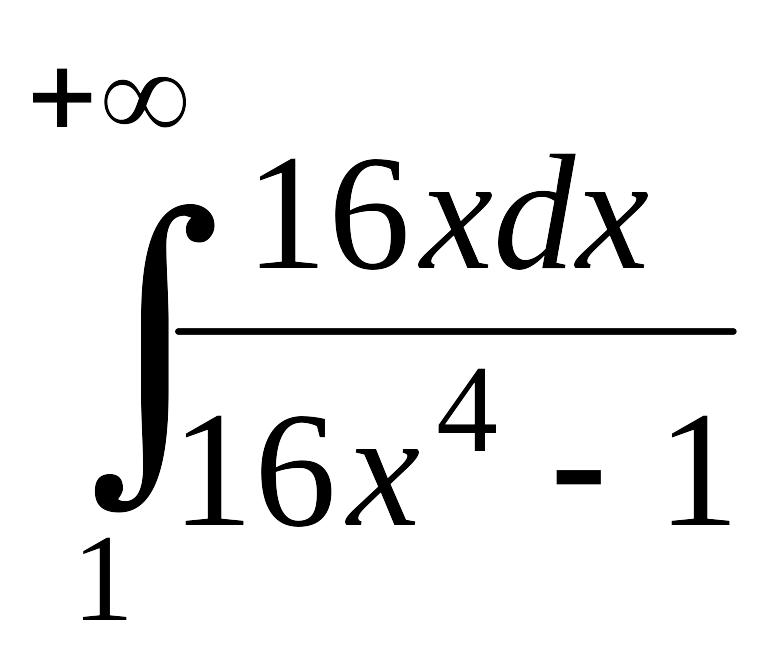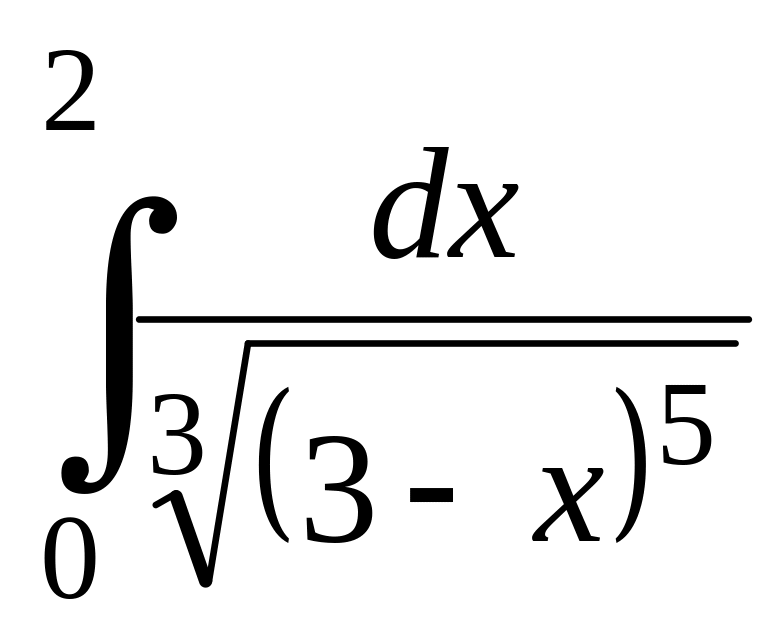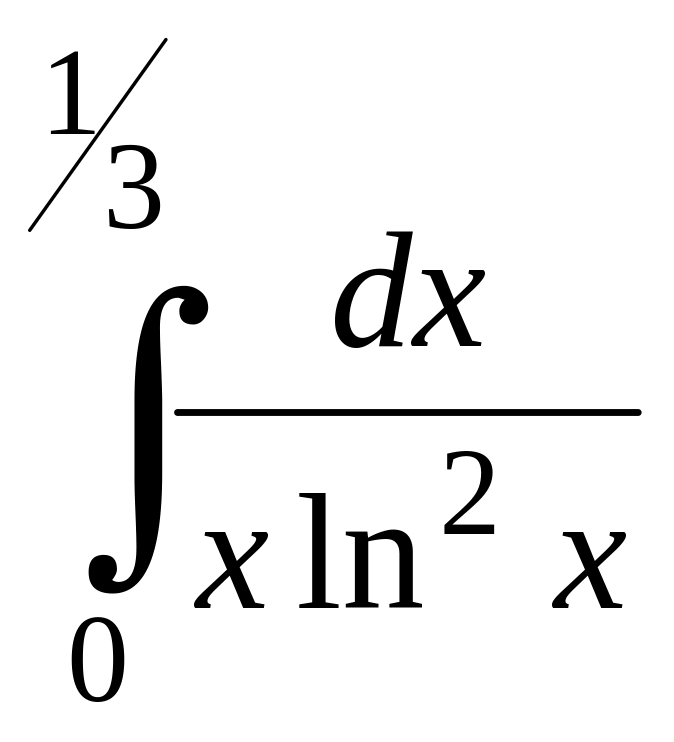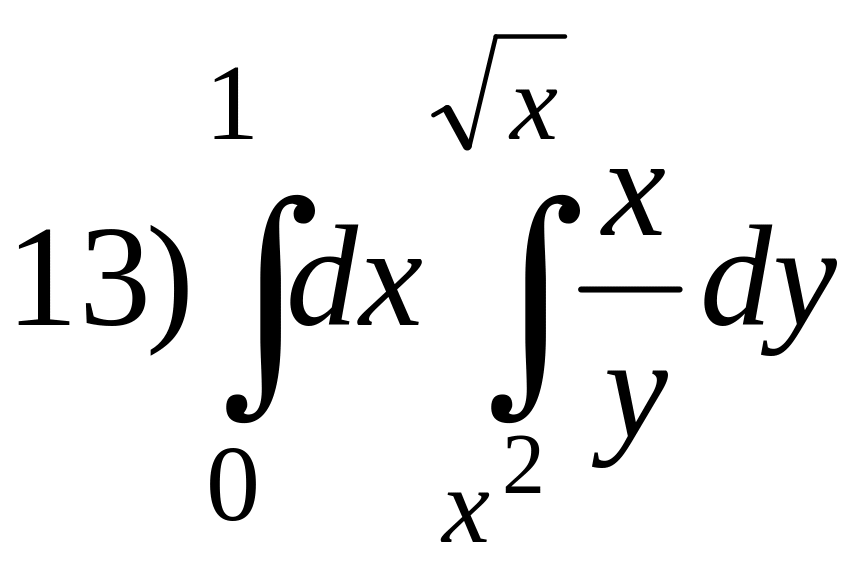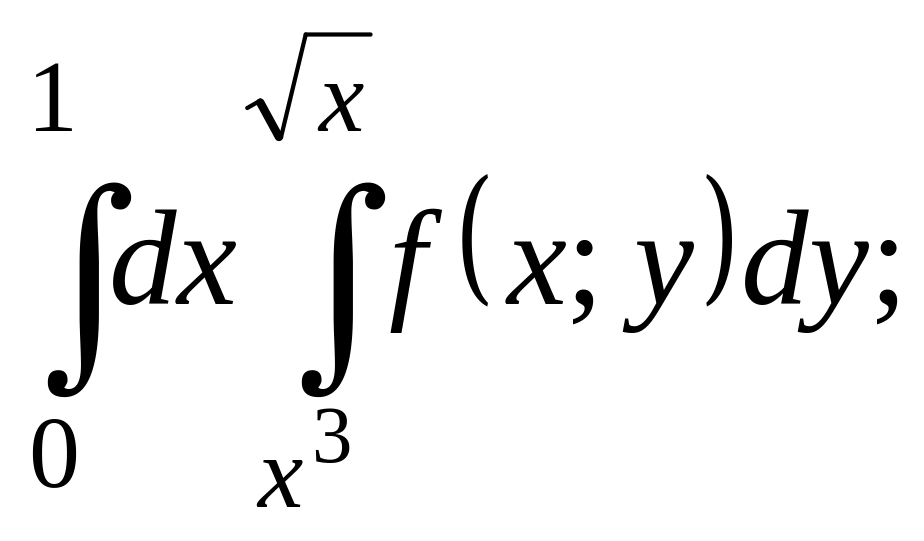
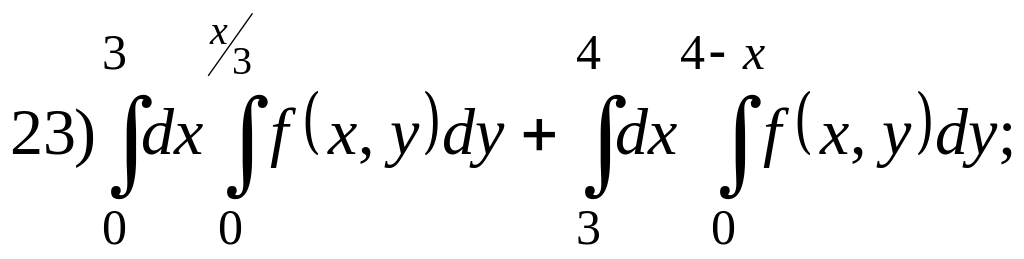
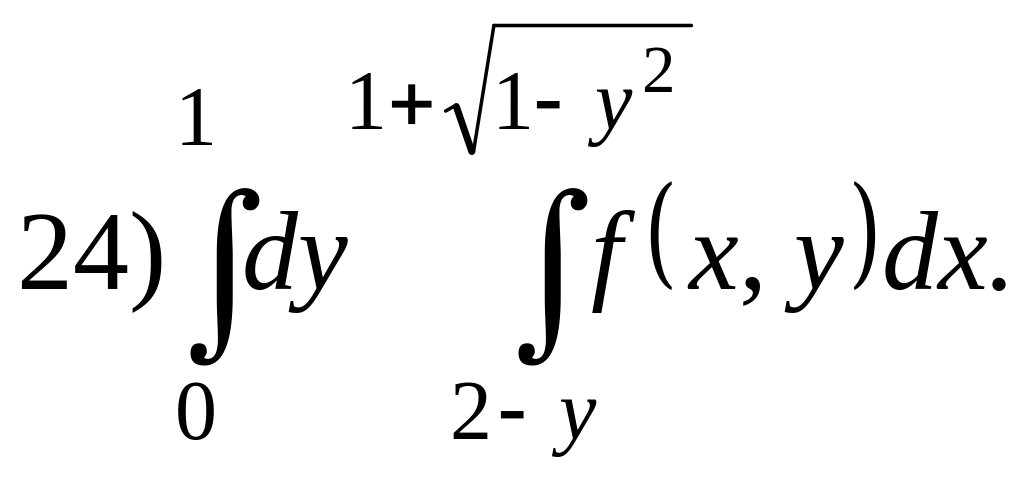