§19. Определенный интеграл

Вычислить:

; ; ; ; ; ; ; ; ; ; ; ;

; ; ; ; ; ; ; ; ; ; ; .

§20, §21 Приложения определенного интеграла.

1. Вычисление площадей плоских фигур

1) Вычислить площадь фигуры, ограниченной прямыми у=3х – 1, х =2, х=4 и осью Ох.

2) Вычислить площадь фигуры, ограниченной кривой у=х³, прямыми х =1, х=2 и осью Ох.

3) Вычислить площадь фигуры, ограниченной кривой , прямыми х =1, х=е и осью Ох.

4) Вычислить площадь фигуры, ограниченной осью Ох и параболой у=х² – 4.

5) Вычислить площадь фигуры, ограниченной осью Ох и параболой у=х² – 3х.

6) Вычислить площадь фигуры, ограниченной параболами и .

7) Вычислить площадь фигуры, ограниченной параболой у=х²–6х+5 и осями координат.

8) Вычислить площадь фигур, ограниченных линиями:

а) ; в) ; б) ; г) ;

д) . е) у2=16х и у=х; ж) ; з)

9) Найти площадь фигуры, ограниченной первой аркой циклоиды

х = a (t – sint), y = a (1 – cost ) и осью Ох (рис.1).

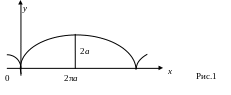
10) Найти площадь круга, заданного параметрическими уравнениями: х = r cost, y = r sint.

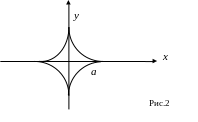
11) Найти площадь фигуры, ограниченной астроидой (рис.2)

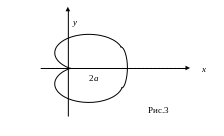
1 2) Вычислить площадь фигуры, ограниченной кардиоидой r=a(1+cos φ) (рис.3).

2. Вычисление объемов тел вращения

1. Найти объем тела, полученного вращением вокруг оси Ох плоской фигуры, ограниченной линиями:

а) у2=8х, у=0, х=2; б) у=х+4, х=0, у=0; в) у=1/х, у=0, х=2, х=3; г) у=х2, у=2х;

д) ху = 5, у=0, х=1, х=5; е) у=2х − х2, у=0; ж) у=− х2 + 3, у=х2 +1.

2) Найти объем тела, полученного вращением вокруг оси Оу плоской фигуры, ограниченной линиями:

а) ; б) ; в) и осью Оу. г) у2=2х, 2х+2у – 3=0;

д) у =х3 , у=0, у=8; е) у= х2, у2=8х; ж) .

3) Вычислить объем тела, полученного вращением вокруг оси Ох плоской фигуры, ограниченной аркой циклоиды

х = a (t – sint), y = a (1 – cost ) и осью Ох (рис.1).

4) Вычислить объем тела, полученного вращением вокруг оси Ох эллипса

х = а cost, y = b sint.

5) Вычислить объем тела, полученного вращением вокруг оси Ох астроиды (рис.2).

3. Вычисление длины дуги плоской кривой

1. Вычислить длину дуги кривой у = ln x от точки х₁= 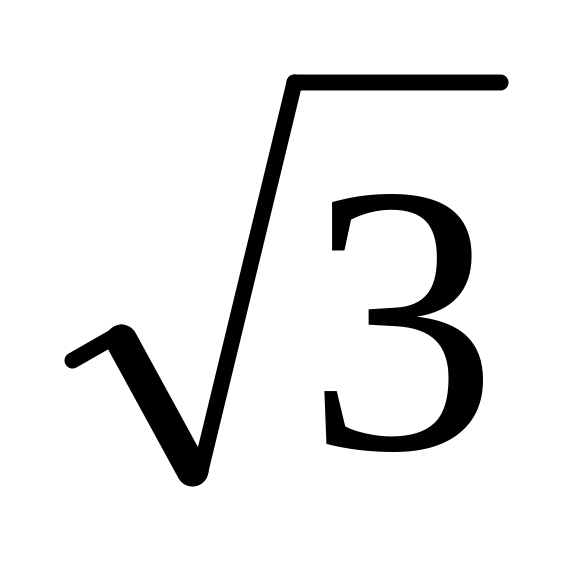до точки х­₂ = .

2. Вычислить длину окружности х² + у² = 25.

3) Найти длину дуги кривой , от точки до точки .

4) Вычислить длину астроиды (рис.2).

5) Вычислить длину окружности .

6) Найти длину кардиоиды (рис. 3).

4. Вычисление площади поверхности вращения

1) Найти площадь поверхности эллипсоида, полученного вращением вокруг оси Ох эллипса .

2) Найти площадь поверхности, образованной вращением вокруг оси Ох дуги кривой от точки х₁=0 до точки х­₂=2 .

3) Найти площадь поверхности, образованной вращением вокруг оси Ох астроиды (рис.2).
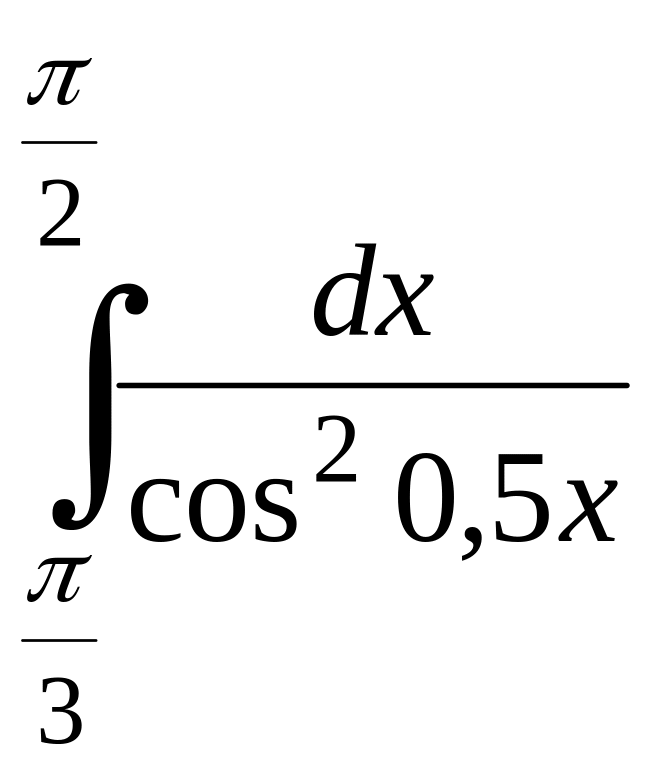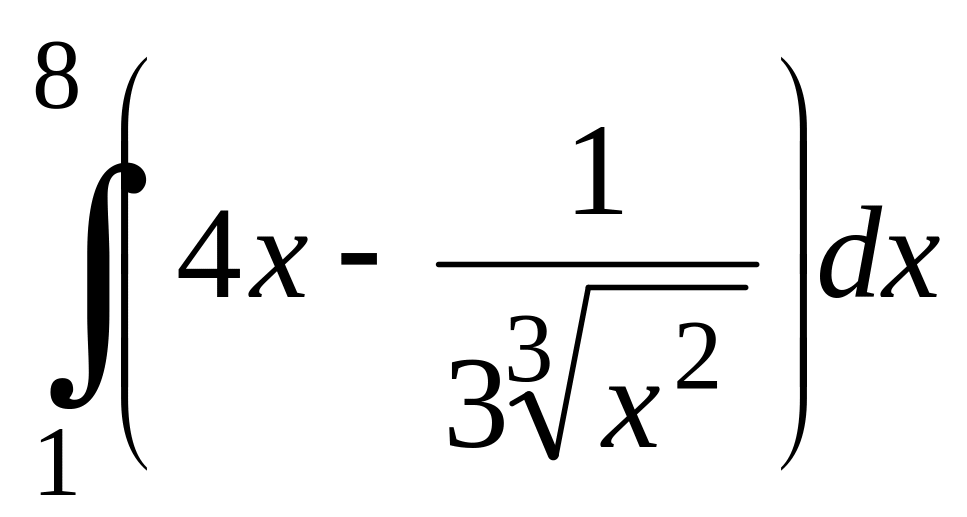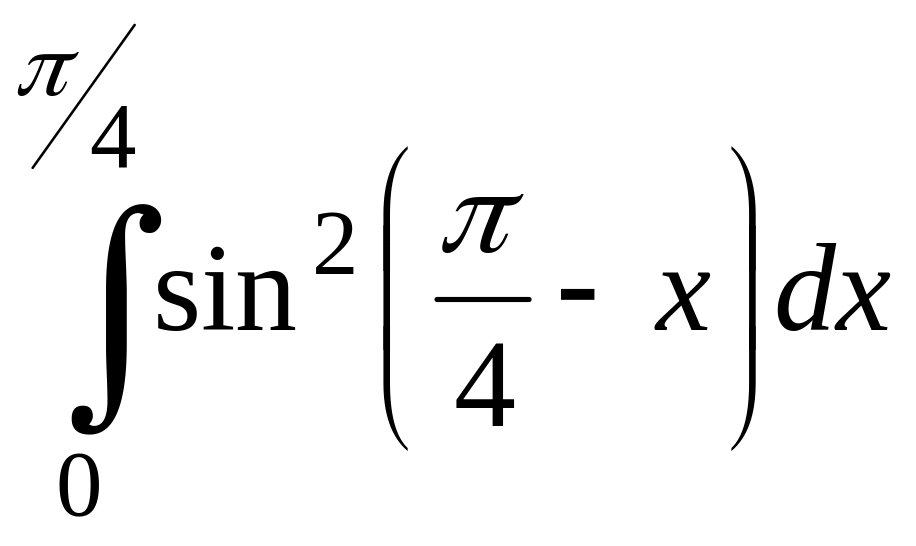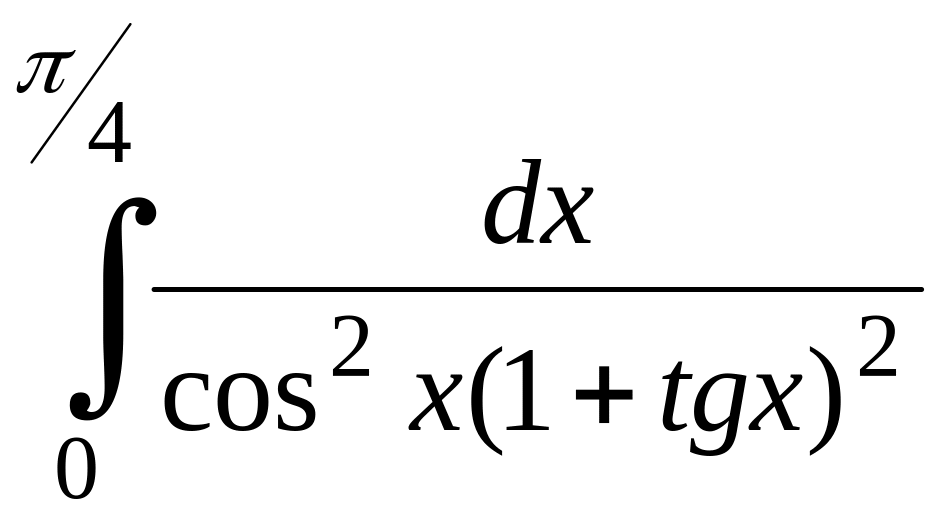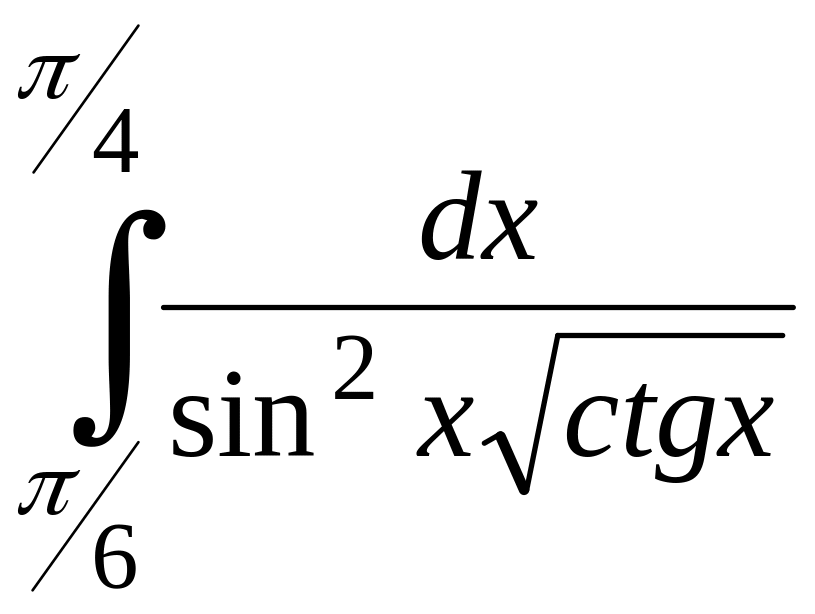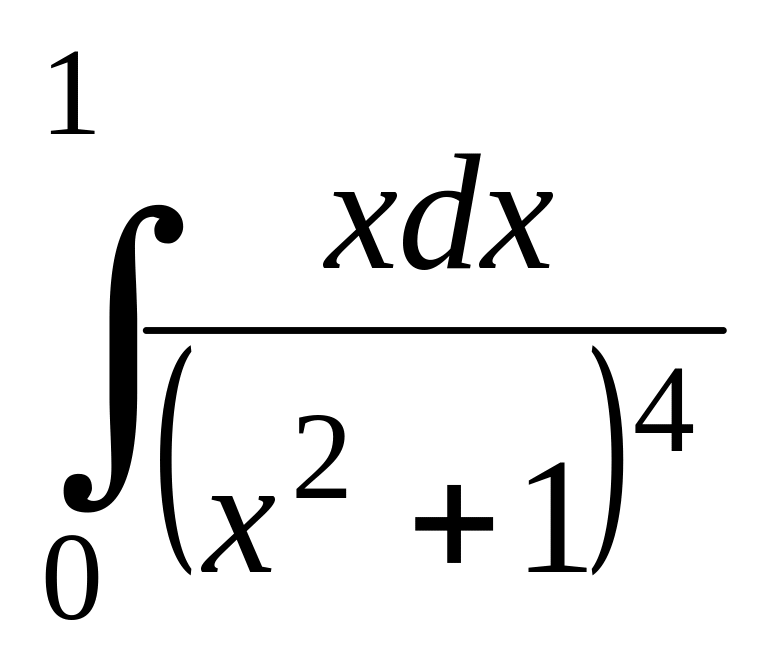
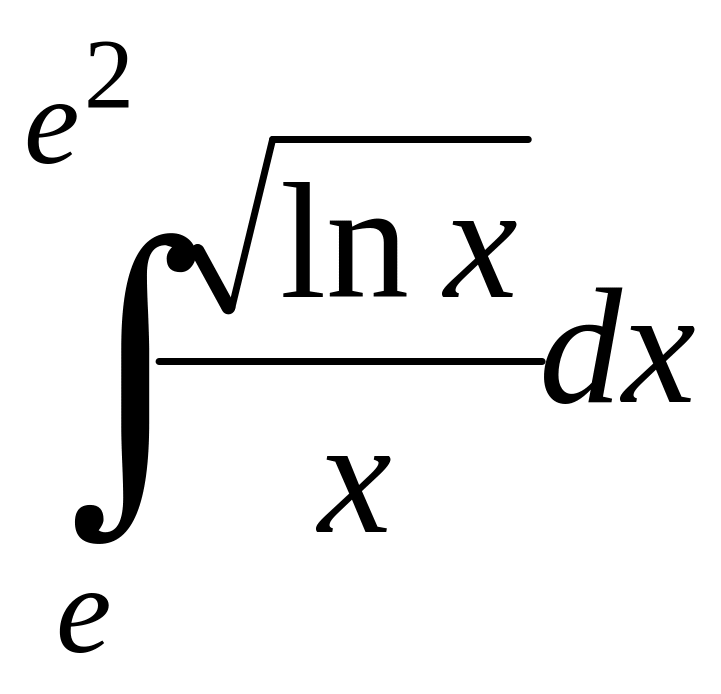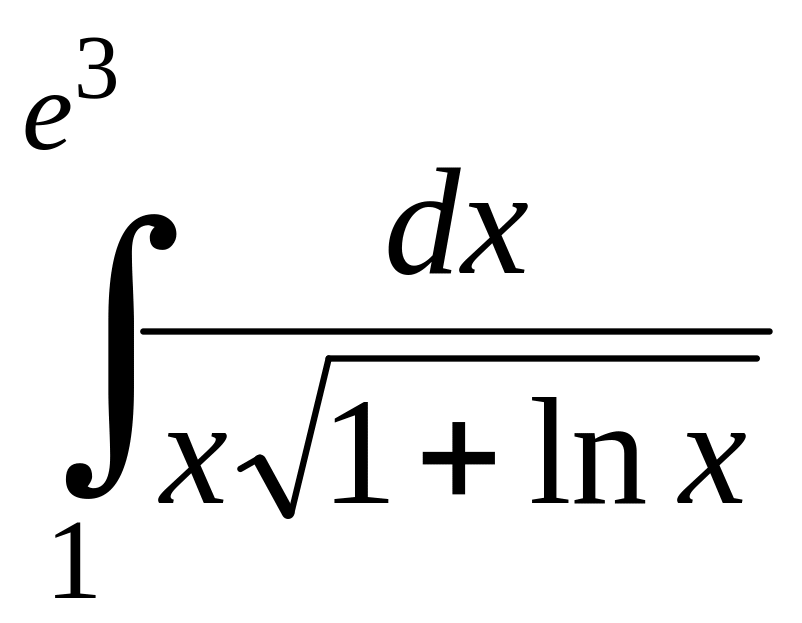