§ 6. Энтропия. Свободная энергия. Энтальпия.
Рассмотрим подробно функции состояния ТД системы и их значение для описания калорических свойств систем. Еще раз отметим, что это величины являются полными дифференциалами от своих параметров, т.е. их изменение зависит только от состояния, а не от пути перехода между этими состояниями. Изменение функции состояния в циклическом процессе равно нулю по определению.
I.) Энтропия.
Рассмотрим
цикл Карно. Пусть одна тепловая машина
работает с идеальным газом, а другая с
другим рабочим телом, причем температуры
нагревателей
и холодильников
этих машин равны. По I теореме Карно КПД
этих машин равны и не зависят от природы
рабочего вещества.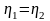 
,
отметим, что
,
тогда
.
Получили
важный результат. Оказывается, что если
не является функцией состояния, и за
цикл не равна нулю
,
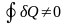то приведенная
теплота
уже является функцией состояния, т.е.
на замкнутом цикле ее изменение равно
нулю. У понятия «приведенная
теплота»
нет наглядного примера, его трудно
как-то представить.
-
- данное тождество называется тождеством Клаузиуса, оно справедливо только для обратимых процессов.
Отсюда следует:
-
- для любого обратимого процесса не зависит от пути, и, следовательно, является функцией состояния.
Эту функцию назвали энтропия. От греческого «энтропос» - возвращение, поворот. Каждое состояние тела характеризуется определенным значением энтропии , подобно тому, как оно характеризуется определенным значением внутренней энергии .
По
определению в интегральной форме
или
в дифференциальной форме
,
.
Тождество Клаузиуса говорит, что при замкнутых обратимых процессах энтропия не меняется.
I
начало ТД для обратимых процессов
можно записать:
,
его еще называют основное ТД тождество.
Рассмотрим, что происходит при необратимых процессах. Возьмем необратимый цикл Карно, для него КПД меньше, чем у обратимого цикла, т.е.
-
для необратимых процессов изменение
отрицательно. Если обобщать для случая
кругового процесса:
-
- неравенство Клаузиуса, для необратимых процессов.
Как изменяется энтропия в необратимых процессах? Рассмотрим циклический процесс. Из состояния 1 в состояние 2 система перешла по необратимому процессу, а из состояния 2 в состояние 1 по другому обратимому процессу.
И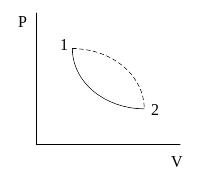
меем
отсюда
Пусть система изолирована, нет обмена энергией с внешней средой , т.е. наше неравенство в левой части станет равным нулю.
В
необратимых процессах для замкнутых
систем энтропия возрастает.
Мы
полагали
!
Если
система обменивается теплотой с внешней
средой, то ее энтропия может вести себя
любым образом.
Р
ассмотрим
еще один пример теплопередачу
от одного тела к другому. Соприкоснулись
два тела.
.
Тело
1 отдало
,
;
тело
2 приняло
,
;
.
Объединим оба тела в систему и посмотрим,
что стало с энтропией, отметим, что
энтропия величина аддитивная:
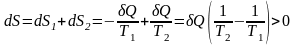
Убеждаемся, что при теплообмене (необратимый процесс), т.е. при передаче количества теплоты от более горячего тела к более холодному, энтропия увеличивается. Реальные необратимые процессы идут таким образом, что изменение энтропии должно быть положительным.
Т.к. , следовательно, энтропия отличает обратимые и необратимые процессы, показывает направления реальных процессов.
Для
необратимых, неравновесных процессов
тождество Клаузиуса превращается в
неравенство:
- это неравенство Клаузиуса для необратимых процессов, которое при полном рассмотрении всех потерь теплоты и работы тоже превращается в равенство.
Еще одна формулировка II начала ТД:
Энтропия
замкнутой системы в необратимых процессах
возрастает. В обратимых процессах
остается постоянной.
Т.о. для обратимого цикла
;
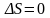для необратимого цикла в изолированных
системах
.
Что же важно:
Энергия сохраняется, поэтому она не может указывать направление процессов. Все реальные процессы необратимы, поэтому в замкнутых системах они идут в направлении возрастания энтропии. Т.о. энтропия указывает направление реальных процессов. Рост энтропии означает все большую недоступность превращения тепла в работу. Максимум энтропии соответствует состоянию равновесия.
Энтропия
экстенсивная величина, она пропорциональна
количеству вещества.
.
Энтропия обладает свойством аддитивности: энтропия системы равна сумме энтропий тел, входящих в систему. Этим свойством так же обладают внутренняя энергия, масса, …. Не обладают этим свойством давление, температура. Физический смысл имеет не сама энтропия, а ее изменение.
Обратимые
адиабатические процессы, для которых
,
характеризуются постоянной энтропией
,
поэтому их можно назвать изоэнтропийные.
Отметим, что более глубокий смысл энтропии вскрывается в статистической физике. Там энтропия связана с понятием термодинамической вероятности состояния системы.
Получим выражение для энтропии - функции состояния одного моля идеального газа. Используем основное ТД тождество, и термическое уравнение состояния идеального газа:
,
учтем
проинтегрировав,
получим общее решение,
,
где
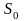- уровень отсчета энтропии.
Мы
убедились, что энтропия идеального газа
является функцией
.
Рассчитаем изменение энтропии при выравнивании температуры двух тел, приведенных в тепловой контакт. Вычисления будут основываться на том, что энтропия является функцией состояния.
Если система перешла из одного состояния в другое посредством необратимого процесса, то логично мысленно перевести систему из первого состояния во второе с помощью некоторого обратимого процесса и рассчитать происходящее при этом изменение энтропии. Оно равно изменению энтропии при необратимом процессе.
Обозначим
массы удельные теплоемкости при
постоянном объеме, и температуры первого
и второго тел соответственно
,
,
и
,
,
.
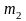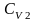При тепловом контакте температуры
выравниваются. Будем считать для
упрощения расчета, что теплообмен
происходить при постоянном объеме
каждого из тел, теплоемкости
и
не зависят от температуры,
.
Тело 1 отдало
,
;
тело 2 приняло
,
;
Для определения температуры
,
которую будут иметь тела по достижении
термодинамического равновесия, можно
написать уравнение
,
с учетом I начала ТД:
,
отсюда
следует, что
В исходном состоянии тела и изолированы друг от друга и имеют разные температуры. Затем они приводятся в тепловой контакт. В результате теплообмена тела приходят в состояние 2. Однако переход из состояния 1 в состояние 2 можно совершить также и с помощью обратимых процессов. В этом случае тела и считаются изолированными, и каждое из них обратимым процессом приводится в состояние 2 при одинаковой температуре . После этого они приводятся в контакт, но это никакого изменения в их состояния не вносит. Таким образом, в обоих случаях начальное и конечное состояния одинаковы, и изменение энтропии можно просчитать с помощью обратимого процесса по формуле определения энтропии:
,
где
.
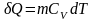Вычислив интегралы, получим:
-
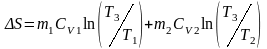это и есть изменение энтропии в необратимом
процессе теплопередачи при постоянном
объеме.