4.2. Задачи и упражнения по главе 3

1. Найдите собственные числа и собственные векторы стохастической матрицы

p₁ q₁

Р = , где p_i + q_i = 1, i = 1,2

q₂ p₂

Преобразуйте их к виду

P = U Λ U^-1,

где Λ - диагональная матрица.

Вычислите Рⁿ при n ->∞ .

2*. Дана стохастическая матрица

Q R

а ) представьте Р в блочном виде Р =

Ø W

б) вычислите матрицу N = (I -Q)^-1;

в) сделайте, спектральное разложение матрицы P = U Λ U^-1;

г) вычислите Р^∞.

3. Процесс описывается неоднородной цепью Маркова, данной на рисунке 4.2.

Вероятности перехода зависят от номера шага к следующим образом:

0.475 + 0.05k 0.025 + 0.95k

Р₁(k) = ———————— ; Р₂ (k) = ———————— ;

0.5+k 0.5+k

Р₃=0.1; Р₄ =0.9;

0.135+ 0.04k 0.015+ 0.36k

Р₅ (k) = ———————— ; Р₆ (k ) = ———————— .

0.15 + 0.4k 0.15 + 0.4k

Оценить:

а) вероятности пребывания процесса в различных cостояниях при к = 1,2,3 ;

б) вероятность завершения процесса за 4 шага;

в) среднее число пребываний процесса в невозвратных состояниях при больших k.

4*. Вычислительный процесс определяется схемой на рисунке 4.3.

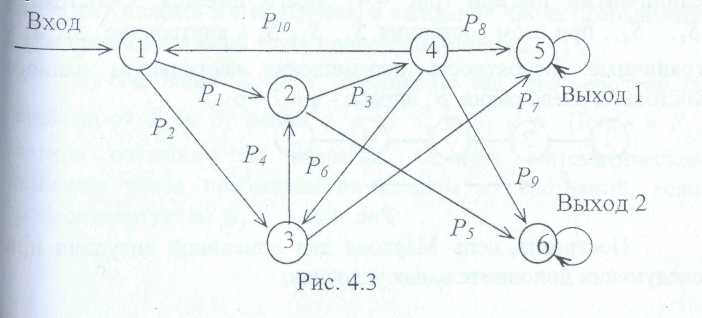
Рассматривая этот процесс как цепь Маркова, определить:

а) вероятность того, что процесс завершится за 3 шага при следующих значениях переходных вероятностей:

о) предельные вероятности завершения процесса по каждому из выходов при значениях вероятностей перехода заданных в п. а);

в) среднее число пребываний процесса в невозвратных состояниях при значениях вероятностей, заданных в п. а);

г) предельную трудоемкость (время выполнения) узла 2 при котором среднее время его выполнения не превысит 5% от суммарного среднего времени выполнения всего процесса. Вероятности переходов определены в п. а), а трудоемкости других узлов следующие:

д) узел, имеющий наибольшее среднеквадратичное отклонение трудоемкости. Вероятности переходов определены в п. а), а трудоемкости узлов следующие:

5. Линейный автомат. Частица движется по прямой единичными шагами (рис 4.4). Всего имеется 5 состояний S₁,...,S₅,, при этом состояния S₂, S₃, S₄ - внутренние, S₁ ,S₅ -граничные. Вероятность перемещения частицы из данного состояния влево равна р , вправо - q = 1 — p.

Построить, цепь Маркова для описанной ситуации при следующих дополнительных условиях:

а) процесс, достигнув S₁ и S₅, остается там навсегда. Оценить математическое ожидание числа пребываний в каждом из состояний, если процесс стартует из S₃;

б) частица, достигнув S₁ или S₅, «отражается» и возвра­щается в состояние, из которого пришла, а попав в S₃, остается там навсегда. Оценить математическое ожидание числа пре­рываний в каждом из состояний, если процесс стартует из S₂;

в) состояния S₁ и S₅ соединены так, что вероятность перехода от S₅ к S₁, равна q, а от S₁ к S₅ - р. Попав в S₃, частица остается там навсегда. Оценить математическое ожидание числа пребываний в каждом из состояний, если процесс стартует из S₁.

6. Условия те же, что и в задаче 5, но перемещение происходит со следующими вероятностями: перемещение влево - р, перемещение вправо - q, отсутствие перемещения - r, р +q+r = 1. Построить цепь Маркова для описанной ситуации при следующих дополнительных условиях:

а) процесс, достигнув S₁ и S₅, остается там навсегда. Оценить математическое ожидание числа пребываний в каждом из состояний, если процесс стартует из S₃;

б) частица, достигнув S₁ и S₅, «отражается» и возвращается в состояние, из которого пришла, а попав в S₃, остается там навсегда. Оценить математическое ожидание числа пребываний в каждом из состояний, если процесс стартует из S₄;

в) состояния S, и S; соединены так, что вероятность перехода от S₅ к S₁ равна q, а от S₁ к S₅ - р. Попав в S₃,

Частица остается там навсегда. Оценить математическое ожидание числа пребываний в каждом из состояний, если процесс стартует из S₅.

7. Решить задачу 5 в предположении, что время изменяется непрерывно, а плотности вероятностей перехода частиц влево равны μ. а вправо – μ₂ ∙ μ₁+μ₂ =μ Построить цепь Маркова для непрерывного времени, написать дифференциальные уравнения для вероятностей пребывания каждом из состояний. Оценить предельные вероятности.

Рассмотреть случаи а), б), в) из задачи 5.

8. Решить задачу 6 для непрерывного времени. Плотности вероятностей перехода частиц влево, вправо и отсутствия перемещения равны, соответственно, μ₁, μ₂, μ₃. Построить цепь Маркова для непрерывного времени, написать дифферен­циальные уравнения для вероятностей пребывания в каждом из состояний. Оценить предельные вероятности.

Рассмотреть случаи а), б), в) из задачи 6.

9. С магнитной ленты считывается массив, состоящий из N блоков данных, с проверкой контрольной суммы по блокам. Вероятность правильного прочтения г-го блока равна р_i. При ошибке чтения делается реверс ленты и новая попытка чтения. Количество попыток не ограничено. Составить сеть Петри, моделирующую эту систему, и соответствующую цепь Маркова. Оценить:

а) математическое ожидание времени чтения массива при N = 100, если для всех блоков р = 0.9, время чтения t_ч-1c, время реверса t_p =0.5c;

б) минимально необходимую вероятность правильного прочтения блока p_min для того, чтобы время чтения массива увеличилось не более чем на 10%, по сравнению со временем Nt_ч, отношение времени чтения и реверса t₄/t_p=4;

в) среднеквадратичное отклонение времени чтения массива от математического ожидания, если для всех блоков р_i=0.95, t_ч=1c, t_p=0.3c, N=200;

г) оценить вероятность правильного прочтения блока р_i, если при чтении 1000 блоков было зафиксировано 5 реверсов.

Принять, что все p_i равны.

10. По информационному каналу с помехами осуществ­ится передача блоков данных в дуплексном режиме от источника И к приемнику П. Это означает, что, получив очередной блок от И, П посылает «квитанцию» И для проверки. Если И подтверждает правильность передачи, то данный блок считается переданным, в противном случае передача повторяется. Число попыток не ограничено. Рассматривая канал как цепь Маркова, где p_i - вероятность правильной передачи И —> П, а р₂ то же для передачи П—>И, оценить;

а) математическое ожидание и дисперсию числа попыток передачи одного блока от И к П;

б) математическое ожидание и среднеквадратичное отклонение времени передачи массива из 100 блоков при P₁ =0.95, р₂=-0.99. время передачи блока от И к П - 0.1с, время передачи «квитанции» от П к И - 0.05с;

в) математическое ожидание и среднеквадратичное отклонение числа повторных передач блоков при N=1000 p₁=0.99, р₂ =0.995;

г) вероятности р₁ и р₂, если известно, что при передаче 1000 блоков было зафиксировано 3 «переспроса». Принять p₁ = p₂.

11. Триггер с тремя входами - R, S, С и двумя выходами y_о и у₁ (рис 4.4) может находиться в двух состояниях:

s₀(y_о =1,y₁= 0) И s,(y₀ = 0,у₁ = 1).

Переход из одного состояния s_j(t_k) в другое s_j(tk=1 )i, j = 0,1 зависит от входного сигнала U(t_k) в момент t_k и определяется следующей схемой:

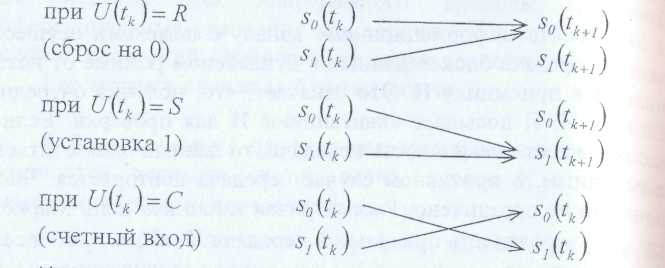
Предположим теперь, что вероятности правильного перехода при входных сигналах R, S, С равны, соответственно, p_r p_s p_с, q_r=1-p_r q_s =1-p_s, q_с= -1-p_с - вероятности ложного срабатывания. Рассматривая последовательность смены состояний s(t₀), s(t₁), s(t₂) (выходное слово) - при последовательности входных сигналов U(t₁), U{t₂) ... (входном слове), оценить:

а) вероятность нахождения триггера в каждом из состояний при входном слове RCRCS , если S(t₀ ) = S₀

б) то же при входном слове RRCCCSS и S(t₀)=S₁;

в) оценить уровень надежности триггера р_s для того, чтобы при 10⁶ срабатываниях по сигналу С вероятность ошибки была бы не больше 10^-5 .

12*. Рассматривается очередь длинной N перед обслуживающим устройством.

На вход системы поступают заявки. Число одновременно поступающих заявок не превышает М .

Устройство в каждый момент времени обслуживает только одну заявку (если очередь не пуста). Количество поступающих на вход очереди заявок ξ, представляет собой - случайную величину со следующим распределением:

Величины а_т заданы и представляют вероятность того, что на вход очереди поступит т заявок. Состояние системы S_i определяется как число заявок i, ждущих обслуживания к началу k-го такта. При этом, если S(t_k) = S_i , то S(t_k+])=S_j

причем

Составить модель системы в виде сети Петри и соответствующую цепь Маркова.

Составить матрицу вероятностей перехода для М = 3, N = 4 и произвести следующие вычисления:

а) вычислить вероятности пребывания в каждом из состояний через 3 шага для следующего распределения вероятностей поступления заявок: a₀₌0.2, a₁=0,3, а₂ =0.3,а₃ = 0.2 . В начальный момент времени очередь была пуста;

б) определить предельные вероятности пребывания системы в каждом из состояний при заданных выше вероятностях;

в) определить среднюю длину очереди для указанных выше условий.

13*. Студент некоторого учебного заведения с четырехгодичным обучением каждый год с вероятность p переходит на следующий курс, с вероятностью q остается на второй год и с вероятностью r отчисляется из института (р + q +r= 1). Составить модель процесса в виде сети Петри и рассматривая процесс перехода с курса на курс как цепь Маркова, определить следующие величины:

а) вероятность того, что студент окончит институт за 4 года. Для расчета положить р = 0.8, q = 0.1, r = 0.1;

б) то же, что и в п. а, но при дополнительном условии, что на каждом курсе нельзя находиться более двух лет;

в)математическое ожидание числа лет пребывания на каждом курсе при условии, что студент поступил на первый курс. Взять данные п. а;

г) дисперсию числа лет пребывания на каждом курсе при условии, что студент поступил на первый курс. Взять данные п. а.

14*. Студент изучает курс в интерактивном режиме с помощью компьютерной системы. Изучение одного модуля (фрагмента курса) состоит из чтения теоретического материала и сдачи тестов. При оценке знаний на «4» и «5» модуль считается освоенным; при оценке «3» студенту дается дополнительный материал и снова проводится тестирование; при оценке «2» студент изучает модуль с самого начала.

1.Составить сеть Петри и цепь Маркова для данной задачи.

2.Определить среднее время изучения модуля, если чтение теоретического материала занимает 1 час, чтение дополнительного материала - 0.5 часа, тестирование - 0.2 часа, вероятность получения оценок «4» и «5» равна p₁, оценки «3» p₂, оценки «2» - рз, (р₁+ р₂+ р₃= 1). Для расчетов взять p₁=0.5, р₂=0.3, р₃=0.2.

15. При реализации двух моделей аппаратуры фирма придерживалась следующих правил:

1.Одновременно продается только одна модель.

2.Если текущий месяц был успешным, то на следующий месяц реализуется та же модель, при этом вероятность успеха сбавляет р₁, вероятность неудачи q₁ =1- р₁.

3. Если текущий месяц был неудачен, то на следующий месяц реализуется другая модель, при этом вероятность успеха оставляет р₂ вероятность неудачи q₂ = 1- р₂.

Составить событийную модель системы в виде сети Петри и, рассматривая процесс реализации аппаратуры как цепь Маркова с двумя состояниями (S₁ - успех и S₂ - неудача), определить следующие характеристики:

а) вероятность успеха и неудачи через 4 шага при условии, что реализация началась с удачи. Для вычислений взять р₁ = 0.5 , р₂ =0.7;

б) вероятность успеха и неудачи через 3 шага при условии, что реализация началась с неудачи. Для вычислений взять р, = 0.45, р, =0.6 ;

в)предельные вероятность успеха и неудачи при большом числе шагов. Для вычислений взять р₁ =0.5, р₂ =0.6 .

16. В условиях задачи 15 известно, что успех после успешного шага приносит доход с₁₁ рублей, неудача после успешного шага - доход с₁₂ рублей, успех после неудачи – с₂₁ рублей, неудача после неудачи - с₂₂ рублей. Определить следующие величины:

а)математическое ожидание полного дохода через 3 шага при условии, что реализация начинается с успеха. Взять Р₁ = O,5 , р₂ = 0.7, с₁₁ = 500 , с₁₂ = 150 , с₂₁ = 200, с₂₂= 400 ;

б)математическое ожидание полного дохода через 4 шага при условии, что реализация начинается с неудачи. Взять числовые данные из п. а;

в)составить в общем виде разностные уравнения для вычисления математического ожидания дохода на п + 1 шаге, если известны математические ожидания дохода на п шаге.

5. Лабораторный практикум

Приведенный ниже цикл из восьми лабораторных работ рассчитан на 34 часа работы в компьютерном классе и примерно на такой же объем самостоятельной работы в компьютерном классе или на домашних компьютерах. Тематика работ, как и вся книга, ориентирована в основном на две методологии моделирования систем.

Первый цикл, состоящий из работ с 1 по 4, связан с моделированием систем на основе методологии сетей Петри. Здесь, помимо собственных программ, которые пишут студенты при выполнении работ, возможно использование программы CPN Tools. Краткая инструкция по работе с этой программой приводится в приложении А.

Аналогично, при исследовании цепей Маркова (работы с 5 по 7) предполагается умение работать с универсальным математическим пакетом MathCad.

Заключительная, восьмая, работа носит творческий характер. Она подводит итог изучению рассмотренных в книге методов моделирования систем и вводит студента в курс моделей и методов прикладного системного анализа и CASE-технологий, которые используются при разработке информационных систем и программного обеспечения.

В случае необходимости по материалам данного лабораторного практикума могут быть сформированы задания по курсовой работе.

Лабораторная работа №1

Моделирование систем с помощью обыкновенных сетей Петри

Цели работы:

1. Освоить основные формализмы обыкновенных сетей Петри (PN);

2. Научиться составлять формальное описание PN, определять инварианты позиций и инварианты переходов;

3. Разработать программу моделирования динамики маркировок и составления слов свободного языка обыкновенных сетей Петри;

4. Провести исследования заданной сети с помощью разработанной программы.

Содержание работы:

1. изучить теоретический материал по учебнику (п. 2.1) или лекциям; получить свой вариант задания;

2. составить программу, моделирующую изменение маркировок и построение свободного языка обыкновенной сети Петри;

3. для заданного варианта задания выполнить следующую работу;

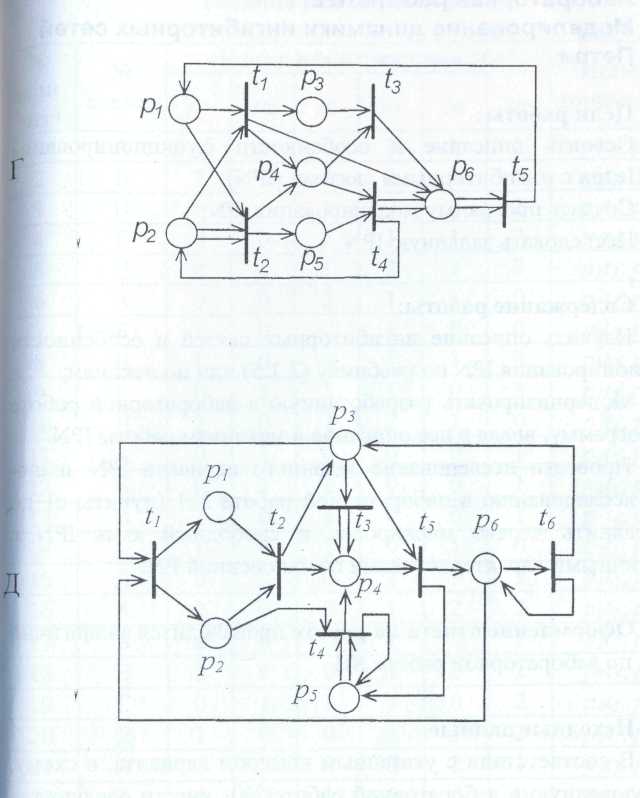
- составить список позиций и переходов, матрицы инцидентности F^p и F^t и начальную маркировку для указанного варианта схемы СП;

• составить матрицу V = (F^t)^t -F^p и найти как минимум по одному инварианту позиций и переходов;

• для начальной маркировки PN, указанной в таблице, с помощью разработанной программы составить дерево ' маркировок на глубину до 5 шагов или до общего числа маркировок, равного 100. При обнаружении повторяющихся маркировок они помечаются значками Мрi, где i – номер обнаруженной повторяющейся маркировки, а построение дерева продолжается только из одной из них. Циклические маркировки, т.е. повторяющиеся на одном пути в дереве обозначаются Mci. Тупиковые маркировки обозначаются М_ti

•выписать все полученные слова свободного языка PN начиная с пустого слова. Аналогично п.2 указать повторения циклы и тупики;

• оценить свойства PN: ограниченность, консервативность безопасность, живость. Проверить соблюдение инвариантов позиций и переходов, найденных в п. 2.

Оформление работы

Оформленный отчет по лабораторной работе должен содержать:

- титульный лист с указанием фамилий исполнителей, группы и номера варианта;

- исходную схему с начальной маркировкой;

-матрицы инцидентности;

- матрицу V u векторы инвариантов;

-дерево маркировок;

-словарь свободного языка PN;

-анализ свойств рассматриваемой PN;

- листинг программы.

Лабораторная работа №2

Моделирование динамики ингибиторных сетей Петри

Цели работы:

1.Освоить описание и особенности функционирования сетей Петри с ингибиторными связями (IPN);

2. Создать программу моделирования IPN;

3.Исследовать заданную IPN.

Содержание работы:

1.Изучить описание ингибиторных связей и особенности функционирования IPN по учебнику (2.1.5) или по лекциям;

2.Модернизировать разработанную в лабораторной работе №1 программу, введя в нее описание и механизм работы IPN.

3.Провести исследование заданного варианта IPN анало­гично исследованию в лабораторной работе №1 (пункты c l по 4). Сравнить дерево маркировок и свободный язык IPN с аналогичными характеристиками обыкновенной PN.

Оформление отчета по работе производится аналогично отчету по лабораторной работе №1.

Исходные данные

В соответствии с указанным номером варианта, в схему, использованную в лабораторной работе №1, внести следующие изменения:

-изменить начальную маркировку в соответствии с приведенной ниже таблицей;

-заменить указанные в последнем столбце таблицы дуги на ингибиторные.

Лабораторная работа № 3

Моделирование систем с помощью раскрашенных сетей Петри

Цели работы

1.Освоить основные формализмы раскрашенных сетей Петри (СPN);

2.Научиться составлять формальное описание CPN;

3.Разработать программу и провести исследование заданной сети путем построения дерева маркировок;

4.Освоить основы работы с программой CPN Tools.

Содержание работы:

1.Изучить теорию CPN по учебнику (п.2.2) или по лекциям.

2. Для указанного варианта задания составить схему и формальное описание CPN. Задания составлены на основе 5 различных задач, каждая задача содержит 5 вариантов условий. Зная свой вариант задания, следует выбрать задачу и соответствующие условия.

3.Разработать программу моделирования динамики CPN.

4.Построить фрагмент дерева маркировок описанной CPN для одного цикла работы моделируемой системы, задав соответствующую начальную маркировку.

5.Построить эквивалентную обыкновенную PN и с помощью разработанной в Лабораторной работе №1 программы получить для нее фрагмент дерева маркировок.

6.С помощью программы CPN Tools создать раскрашенную сеть в соответствии с и.2 . задания и проверить ее работоспособность.

Оформление работы

Оформленный отчет по лабораторной работе должен содержать:

•титульный лист с указанием фамилий исполнителей, группы и номера варианта;

•задание -по работе;

•схему CPN,построенную с помощью программы CPN Tools;

• формальное описание CPN;

• дерево маркировок CPN;

• схему эквивалентной обыкновенной PN;

• дерево маркировок обыкновенной PN, полученное с помощью программы;

• листинг программы моделирования CPN.

Задача 1

В цеху собирается изделие, состоящее из К деталей типа А , М деталей типа В , N деталей типа С. Детали поступают в цех с участка комплектования в указанном ниже порядке. Собранное изделие поступает на склад емкостью S изделий, а со склада - на продажу потребителю. При отсутствии комплекта деталей и заполнении склада работа цеха останавливается.

Дополнительные условия:

1. Детали поступают на сборку по одной в определенном порядке: сперва типа А , затем типа В , затем типа С;

2. Детали поступают на сборку комплектами: К деталей типа А, М - типа В, N - типа С.

Задача 2

Система массового обслуживания содержит два типа устройств: А и В и выполняет заявки k видов. Устройств А - п_A экземпляров, устройств В - п_B экземпляров. Заявки поступают извне в буфер заявок и обслуживаются в указанном ниже порядке, обслуженные заявки выводятся из системы.

Устройство типа А обслуживает все заявки, устройство типа В - только заявки первого и k-го видов. Дополнительные условия:

1. Заявки поступают произвольном порядке, а выводятся из системы в том же порядке, что и поступили;

2. Заявки имеют приоритеты: сперва обслуживаются все находящиеся в буфере заявки первого вида, затем все заявки второго вида и т.д.

Задача 3

Система распределенной обработки информации состоит из главного процесса М (Master) и N подчиненных процессов (Slave) S₁,..., S_n. Перед началом работы М посылает всем подчиненным процессам запрос на тестирование и продолжает работу только с теми из них, кто прислал положительные ответы на тесты.

Работа заключается в обмене сообщениями: М посылает процессу Si n_i сообщений в синхронном или асинхронном режиме (т.е. с приемом «квитанций» о получении сообщения или без нее).

Порядок обмена сообщениями может быть:

1. произвольный;

2. в порядке возрастания номеров Si,

3. все сообщения, относящиеся к Si, передаются подряд;

4. режим обмена синхронный;

5. режим обмена асинхронный.

Задача 4

По компьютерной сети передается сообщение от отправителя S (Sender) к получателю R (Receiver). Сообщение разбито на М пакетов p_i (i=1,...,M), в сети существует N маршрутов передачи m_j (J=1,...,N). Каждый пакет р_i может быть передан по любому из маршрутов m_j, причем скорость передачи может быть различной.

Принятые пакеты получатель R записывает в буфер в порядке их поступления, а затем выводит по порядку номеров для того, чтобы получить исходное сообщение.

Дополнительные условия:

1. Емкость буфера получателя R составляет К пакетов. При заполнении буфера получатель R прекращает прием пакетов;

2. То же, что и в п. 1, но при наполнении буфера отправитель S прекращает посылку пакетов;

3. Пакеты передаются по одному, и передача очередного пакета p_i+1 возможна только после

получения «квитанции» о приеме предыдущего пакета p_i.

Задача 5

Арифметическо-логическое устройство процессов содержит конвейер команд, состоящих из N видов функциональных устройств и обеспечивающий выполнение М различных команд (п. 2.3.1). Некоторые функциональные устройства могут дублироваться, в этом случае они работают параллельно. При поступлении из ОЗУ команды определенного типа конвейер настраивается на ее выполнение и пропускает операнды последовательно через все функциональные устройства. Если следующие команды имеют тот же тип, то конвейер не перестраивается, а выполняет их в прежнем режиме, загружая последовательно все функциональные устройства. При поступлении команды другого типа ее выполнение блокируется до тех пор пока не будет завершено выполнение предыдущих команд, и конвейер не освободится. После этого происходит перестройка, конвейера на новый тип команд и работа по описанному выше алгоритму.

Принятые допущения:

1. Конвейер рассматривается как простая очередь (рис. 4.1), образованная функциональными устройствами (с учетом их дублирования);

2. При прохождении команд через дублированные функциональные устройства не должна нарушаться их очередность - правило FIFO.

3. Необходимо составить начальную маркировку, соответствующую тестовой последовательности команд.

Лабораторная работа № 4

Исследование раскрашенных сетей Петри с временным механизмом

(Цели работы:

1. Освоить описание и особенности функционирования раскрашенных сетей Петри с временным механизмом (timed CPN - tCPN);

2.Создать программу моделирования tCPN;

3 Освоить методику имитационного моделирования системы, описанной с помощью tCPN.

Содержание работы:

1. Изучить описание и особенности функционирования tСPN по учебнику (2.2.4 п. 2) или по лекциям.

2. Расширить возможности CPN, созданной в лабораторной работе №3, за счет введения временного механизма. Для этой цели ввести случайные времена задержки срабатывания переходов.

3. Внести необходимые изменения в сеть, созданную в лабораторной работе №3, с помощью CPN Tools.

4. Модифицировать программу созданную в лабораторной работе №3, путем учета времени задержки срабатывания переходов.

5. Провести имитационное моделирование полученной системы и определить критические узлы, ограничивающие быстродействие системы. Во всех задачах все времена задержки считать распределенными по равномерному закону.

Оформление работы

Оформленный отчет по лабораторной работе должен содержать:

• титульный лист с указанием фамилий исполнителей, группы и номера варианта;

• задание по работе;

• схему CPN с временными отметками, полученную с помощью CPN Tools;

• результаты имитационного моделирования;

•листинг программы моделирования tCPN.

Задача 1

В системе, рассмотренной в лабораторной работе №3 учесть следующие временные задержки (в часах).

1. Провести имитационное моделирование процесса выпуска и реализации 200 изделий, суммируя временные задержки на каждом этапе процесса.

2. Оценить среднее время изготовления и реализации одного изделия и его.дисперсию.

3. Оценить наиболее «узкое место» в процессе производства и реализации.

Задача 2

В системе, рассмотренной в лабораторной работе №3, учесть следующие временные задержки (в секундах).

1. Провести имитационное моделирование процесса обслуживания по '100 заявок каждого вида. Для каждой заявки просуммировать временные задержки на всех этапах.

2. Оценить среднее время обслуживания одной заявки и его дисперсию.

Задача 3

В системе, рассмотренной в лабораторной работе №3, учесть следующие временные задержки (в секундах).

1. Провести имитационное моделирование процесса обмена 100 сообщениями с каждым из подчиненных процессов S_i. Для каждого обмена суммируются временные задержки на всех этапах.

2. Для каждого из процессов Si оценить среднее время одного обмена и его дисперсию.

Задача 4

В системе, рассмотренной в лабораторной работе №3, учесть следующие временные задержки (в миллисекундах).

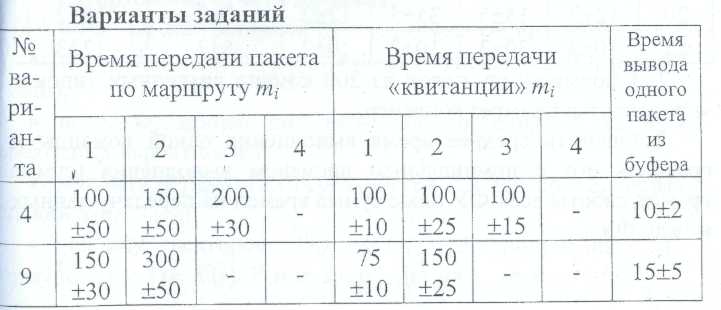
1. Провести имитационное моделирование процесса передачи 100 сообщений, каждое из которых состоит из 8 пакетов.

2. Оценить среднее значение и дисперсию времени передачи одного пакета.

Задача 5

В системе, рассмотренной в лабораторной работе №3, учесть следующие временные задержки (в микросекундах).

1. Сформировать поток из 200 команд различных типов и «пропустить» их через конвейер.

2. Оценить среднее время выполнения одной команды и сравнить его с номинальным временем выполнения (сумма времен, работы всех ФУ плюс сумма времен на передачу данных между ФУ).

Лабораторная работа № 5

Моделирование динамики систем на основе

цепей Маркова с дискретным временем (часть 1)

Цели работы:

1. Освоить основные положения теории конечных цепей Маркова (ЦМ) с дискретным временем;

2.Научиться составлять ЦМ для моделирования вычислительных систем и анализа динамики их функционирования;

3.Провести имитационное моделирование динамики ЦМ.

Содержание работы:

1. Изучить теоретический материал по ЦМ по учебнику (п. 3.1) или лекциям;

2.Для заданного варианта модели вычислительной системы составить матрицу переходных вероятностей;

3.Вычислить с помощью написанной программы или пакета MathCad векторы вероятностей X(t) пребывания системы в каждом из состояний для 15 шагов при старте из заданного входного состояния и построить соответствующие графики;

4.Составить алгоритм имитационного моделирования динамики ЦМ, написать и отладить программу на языке высокого уровня. Один из возможных вариантов алгоритма приведен ниже;

5. Провести статистическое моделирование динамики ЦМ и сравнить их с результатами п.4.

Оформление отчета по работе

Отчет по лабораторной работе должен содержать:

• титульный лист с указанием всех исполнителей и номера группы;

• исходные данные по ЦМ - граф состояний и матрицу переходных вероятностей;

•матрицу переходных вероятностей Р и вектор начальных условий Х(0);

• таблицу векторов X(t), t=0,1,...15, полученных по формуле X(t + 1) = X(t)-P и график хj(t ), ,j=1....n, t=0,...l5;

•листинг программы имитационного моделирования ЦМ-

•таблицу векторов X(t), полученных с помощью имитационной программы при различном числе экспериментов (N=100, 1000, 2000) и график x_j{t), ,j=1,...n, t=0,...15. Оценить влияние числа N на точность имитационного моделирования.

Алгоритм имитационного моделирования цепи Маркова

Задано:

a) матрица переходных вероятностей Р;

b) номер стартового состояния jo;

c) число временных шагов исследования процесса t_k;

d) число статистических экспериментов N.

Требуется: вычислить оценки вероятностей нахождения процесса в различных состояниях X[j] в момент времени t=t_k

Алгоритм

1.Создаем два массива X и Y длиной п. Заполняем массив X нулями, полагаем t_k= 1

2.Полагаем t =0 и помещаем 1 в позицию jo массива Y, остальные элементы этого массива - нули.

3.Выполняем основной шаг алгоритма - определяем номер очередного состояния j. Прибавляем 1 к элементу Y[J]. Увеличиваем t на 1.

4.Повторяем шаг 3 до тех пор, пока t < t_k.

5.Пересчитываем X:=X+Y.

6.Повторяем шаги 2 - 5 N раз.

7.Вычисляем значения X[j]=Х[j]/N, j=1,..N, которые являются оценками среднего числа пребываний процесса в j-м состоянии.

п

8. Вычисляем сумму S = ∑X[j] и величины Х[j]/S, которые представляют собой оценки

j=1

вероятностей пребывания процесса в каждом состоянии. Выводим время t_k и вектор X на печать и на график.

9. Повторяем шаги 1-7 для всех t_k, k = 1,...,15.

Основной шаг алгоритма

Пусть в момент времени t система находится в состоянии S_k . Определим номер состояния, в которое система перейдет в момент t+1. Выделим k-ю строку матрицы Р:

С помощью датчика случайных чисел генерируем случайное число r(t), 0≤r{t)≤1 с равномерным законом распределения. Тогда номер состояния j определится условием:

j

Иными словами, j - это номер элемента строки р_k , для которого сумма ∑ р_ks при возрастании

s=1

j от 1 до п впервые не меньше r(t).

Исходные данные к работе

Исходные данные представлены в виде таблицы и набора схем. По указанному преподавателем номеру варианта в таблице выбирается соответствующая строка. Второй столбец таблицы указывает код схемы и стартовое состояние (например, Г1 -схема Г, старт происходит из состояния S1). Далее указаны вероятности перехода между состояниями в десятых долях (т.е. указанное в таблице, значение Р₁=- 4 означает, что P₁=0,4). Этими вероятностями помечены дуги на схеме. Некоторые дуги не помечены – соответствующие вероятности определяются из условия, что сумма вероятностей на дугах, отходящих от каждого узла, равна единице. Следующая группа столбцов задает трудоемкости отдельных процессов С_i- в секундах.

В последнем столбце указаны величины μ_мах (1/с), которая используется в лабораторной работе №7.

Лабораторная работа № 6

Моделирование динамики систем на основе

цепей Маркова с дискретным временем (часть 2)

Цели работы:

1. Освоить основные положения теории конечных цепей Маркова (ЦМ) с дискретным временем;

2. Научиться составлять ЦМ. для моделирования вычис­лительных систем и анализа динамики их функционирования;

3. Провести расчет характеристик производительности вычислительных систем с использованием пакета MathCad.

Содержание работы:

1. Изучить теоретический материал по ЦМ по учебнику (п. 3.1-3.5) или лекциям;

2. Для системы, заданной в лабораторной работе №5, провести следующие вычисления:

2.1. Структурировать матрицу Р, выделить множества невозвратных и эргодических состояний Т и Ť. Выписать матрицы Q, W, R;

2.2. Вычислить среднее число тактов пребывания процесса в каждом из невозвратных состояний путем вычисления матрицы N = (E- Q)^-1;

2.3. На основе матрицы N вычислить среднюю трудоемкость вычислительного процесса С_г ;

2.4. Получить оценку строки матрицы N, соответствующей заданному стартовому состоянию с помощью модификации программы, составленной в лабораторной работе №5. Модификация алгоритма заключается в следующем:

1) Выполнение шага 3 прекращается, если очередное состояние Sj относится к эргодическому множеству: S_j Ť;

2) Исключается шаг 8, на печать выводится результат шага 7;

3) Расчет ведется только для максимального значения t_k ,k = 20;

2.5. Оценить среднеквадратичное отклонение от среднего числа пребываний процесса в множестве невозвратных состояний D¹¹², где D = N(2N_dg—E)—N_sq и соответствующее среднеквадратичное отклонение трудоемкости вычислений от среднего σ_Θ;

2.6). Оценить предельные вероятности пребывания процесса в множестве эргодических состояний.

Оформление отчета по работе

Отчет по лабораторной работе должен содержать:

• титульный лист с указанием всех исполнителей и номера группы;

• исходные данные по ЦМ - граф состояний и матрицы переходных вероятностей Р; Q; W;

• матрицу средних значений N и оценку средней трудоемкости процесса С_∑;

• оценку строки матрицы N, полученную путем имитационного моделирования;

• матрицу дисперсий D и оценку среднеквадратичного отклонения трудоемкости σ_Θ;

• листинг модифицированной программы имитационного моделирования ЦМ с подсчетом среднего числа пребываний процесса в различных состояниях;

• оценки предельных вероятностей пребывания процесса в состояниях эргодического множества:

а) путем прямого возведения матрицы Р в высокую степень;

б) путем спектрального разложения матрицы.

Лабораторная работа № 7

Моделирование динамики систем на основе

Цепей Маркова с непрерывным временем

Цели работы:

1. Освоить основные положения теории конечных цепей Маркова (ЦМ) с непрерывным временем;

2. Научиться составлять и исследовать модели вычислительных систем на основе этой теории.

Содержание работы:

1. Изучить теоретический материал по учебнику (п. 3.6) или лекциям.

2. Создать ЦМ с непрерывным временем на базе модели, рассмотренной в Лабораторных работах №6 и №7. Для этого:

• по заданному номеру варианта из таблицы в лабораторной работе №5, взять величину μ_maх и для всех дуг графа цепи Маркова рассчитать плотности вероятностей переходов μ.. = p_ij ∙ μ_mах;

• Составить матрицу ТС (формула (3.42));

• Составить уравнение Колмогорова в матричной и компонентной формах для определения динамики изменения вектора вероятностей X(t). Задать начальные условия исходя из заданного стартового состояния системы;

3. Решить уравнение Колмогорова с заданными начальными условиями с помощью пакета MathCad. Решение вести до получения установившихся значений вектора X(t). Оценить временную шкалу решения исходя из величины μ_mах. Сравнить график решения с аналогичным графиком, полученным в к лабораторной работе №5, п. 3.

4. Вычислить установившиеся значения вектора X(t) путем решения системы линейных уравнений, полученных из уравнения Колмогорова при dX(t)/dt = 0 с учетом условия

n

∑x_i(t) = l. Сравнить решение с результатом п. 3.

i=1

Оформление отчета по работе

Отчет по лабораторной работе должен содержать:

• титульный лист с указанием всех исполнителей и номера группы;

• исходные данные по ЦМ - граф состояний с указанием плотностей вероятностей переходов μ_ij;

• матрицу ;

• уравнение Колмогорова в матричном и компонентном виде и начальные условия;

• график решения - все компоненты вектора X(t) с разметкой временной шкалы;

• систему уравнений для вычисления установившегося значения X(t) и ее решение.

Лабораторная работа № 8 Разработка и исследование модели деятельности

Цели работы:

1. Научиться строить событийные модели определенных видов деятельности (бизнес-процессов) на основе формализмов сетей Петри с использованием структурного подхода;

2. Составить вероятностную модель функционирования заданной системы как цепи Маркова и исследовать характеристики ее функционирования;

3. Сопоставить полученные модели с моделями, полученными на основе диаграмм потоков данных DFD.

Содержание работы:

1. Доставить словесное описание заданной деятельности (по номеру варианта);

2. Изучить основные положения методологии диаграмм потоков данных DFD и построить для заданной деятельности контекстную диаграмму и детализирующие диаграммы первого уровня;

3. Выделить в полученном описании условия и события;

4. Составить сеть Петри, моделирующую описанную систему, с использованием программы CPN Tools, определить начальную маркировку;

5. Составить дерево маркировок полученной сети Петри;

6. Выделить на дереве маркировок фрагменты, которые можно рассматривать как состояния системы и составить цепь Маркова, описывающую переходы между состояниями;

7. Задаться численными значениями вероятностей перехода и рассчитать (в зависимости от вида полученной системы): средние времена функционирования системы, предельные вероятности нахождения системы в состояниях эргодического множества и др.

Оформление отчета по работе

Отчет по лабораторной работе должен содержать:

• титульный лист с указанием всех исполнителей, номера группы и варианта задания;

• словесное описание функционирования системы;

• DFD - диаграммы моделируемой системы;

• список условий и событий в системе;

• сеть Петри описывающую функционирование системы;

• дерево маркировок сети Петри;

• цепь Маркова, составленную на основе дерева маркировок;

• матрицу вероятностей перехода между состояниями;

• численные оценки показателей функционирования системы: средние времена, средние трудоемкости, предельные вероятности (в зависимости от вида системы).

Приложение А

Краткая инструкция по созданию сетей Петри в системе CPN Tools

Настоящая инструкция составлена на основе фирменного руководства CPN Tools Manual, которое прилагается к пакету CPN Tools (http://www.daimi.au.dk/CPnets/CPN2000).