Источники магнитного поля

Магнитное поле создается (порождается) током заряженных частиц, или изменяющимся во времени электрическим полем, или собственными магнитными моментами частиц (последние для единообразия картины могут быть формальным образом сведены к электрическим токам).

Закон Био́—Савара—Лапла́са — физический закон для определения вектора индукции магнитного поля, порождаемого постояннымэлектрическим током. Был установлен экспериментально в 1820 году Био и Саваром и сформулирован в общем виде Лапласом. Лаплас показал также, что с помощью этого закона можно вычислить магнитное поле движущегося точечного заряда (считая движение одной заряженной частицы током).

Для тока текущего по контуру (тонкому проводнику)

Пусть постоянный ток   течёт по контуру (проводнику) , находящемуся в вакууме,   — точка, в которой ищется поле, тогда индукция магнитного поля в этой точке выражается интегралом (в системе СИ)

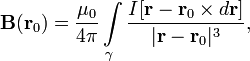
где квадратными скобками обозначено векторное произведение, r - положение точек контура  , dr - вектор элемента контура, вдоль которого идет проводник (ток течет вдоль него);   - константа (магнитная проницаемость вакуума).

Если же взять за точку отсчёта точку, в которой нужно найти вектор магнитной индукции, то формула немного упрощается:

где   - вектор описывающий кривую проводника с током  ,   - модуль  ,   - вектор магнитной индукции, создаваемый элементом проводника  .

Направление   перпендикулярно плоскости, в которой лежат вектора   и  . Направление вектора магнитной индукции может быть найдено по правилу правого винта: направление вращения головки винта дает направление  , если поступательное движение буравчика соответствует направлению тока в элементе. Модуль вектора   определяется выражением (в системе СИ)

Векторный потенциал даётся интегралом (в системе СИ)

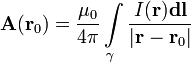
[Править]Для распределенных токов

Для случая, когда источником магнитного поля являются распределенные токи, характеризуемые полем вектора плотности тока j, формула закона Био — Савара принимает вид (в системе СИ):

где j = j(r), dV - элемент объема, а интегрирование производится по всему пространству (или по всем его областям, где j≠0), r - соответствует текущей точке при интегрировании (положению элемента dV).

Векторный потенциал:

 Закон полного тока (для магнитного поля в вакууме)

где ₀ — магнитная постоянная;   — алгебраическая сумма токов, охватываемых контуром; п — число токов.

Закон полного тока (для произвольной среды)

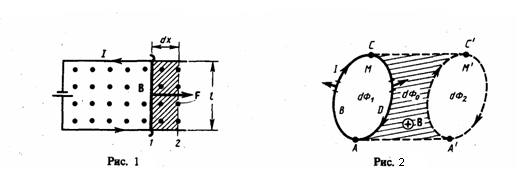
  ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ПРОВОДНИК С ТОКОМ

Магнитное  поле  действует  с  некоторой  силой  на  любой  проводник  с  током,  находящийся  в  нем. Если проводник, по которому протекает электрический ток подвесить в магнитном поле, например, между полюсами магнита, то магнитное поле будет действовать на проводник с некоторой силой и отклонять его.

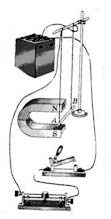
Направление  движения  проводника  зависит  от  направления  тока  в  проводнике  и  от   расположения  полюсов  магнита. Действие  силы на рамку с током.

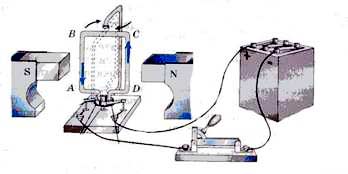Если поместить проволочную рамку , по которой протекает электрический ток, в магнитное поле,  то в результате действия силы магнитного поля, рамка будет поворачиваться.

Действие магнитного поля на контур с током

Для удобства предположим, что контур имеет прямоугольную форму.

1) Пусть dl перпендикулярен B, т. е. любой элемент контура перпендикулярен силовым линиям. Cилы Ампера, действующие на каждый прямолинейный участок контура, указаны на рисунке.

Если контур с током расположен перпендикулярно силовым линиям, то действие поля выражается в сжимании и разжимании контура. Если же контур состоит из упругого проводника, то внешнего изменения положения в пространстве не будет.

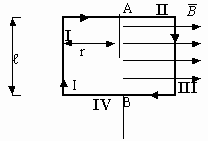
2) площадь контура с током параллельна силовым линиям. То есть нормаль плоскости контура перпендикулярна вектору магнитной индукции.

Тогда силы Ампера на каждом участке:

I. Sin=1, F_A≠0, сила направлена от нас.

II, IV. Sin=0, F_A=0, То есть на элемент контура с током лежащим вдоль силовых линий F_A не действует.

III Sin=1, F_A≠0, сила направлена к нам. Тогда если контур с током закрепить в точках A и B ,то при таком расположении его в магнитном поле он будет вращаться, то есть на него действует момент силы.

Магни́тный пото́к — поток   как интеграл вектора магнитной индукции   через конечную поверхность  . Определяется через интеграл по поверхности

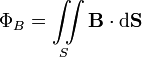
при этом векторный элемент площади поверхности определяется как

где   — единичный вектор, нормальный к поверхности.

Также магнитный поток можно рассчитать как скалярное произведение вектора магнитной индукции на вектор площади:

где α — угол между вектором магнитной индукции и нормалью к плоскости площади.

Магнитный поток через контур также можно выразить через циркуляцию векторного потенциала магнитного поля по этому контуру:

Работа по перемещению проводника и контура с током в магнитном поле

На проводник с током в магнитном поле действуют силы, которые определяются с помощью закона Ампера. Если проводник не закреплен (например, одна из сторон контура сделана в виде подвижной перемычки, рис. 1), то под действием силы Ампера он в магнитном поле будет перемещаться. Значит, магнитное поле совершает работу по перемещению проводника с током.  Для вычисления этой работы рассмотрим проводник длиной l с током I (он может свободно двигаться), который помещен в однородное внешнее магнитное поле, которое перпендикулярно плоскости контура. Сила, направление которой определяется по правилу левой руки, а значение — по закону Ампера, рассчитывается по формуле    Под действием данной силы проводник передвинется параллельно самому себе на отрезок dx из положения 1 в положение 2. Работа, которая совершается магнитным полем, равна    так как ldx=dS — площадь, которую пересекает проводник при его перемещении в магнитном поле, BdS=dФ — поток вектора магнитной индукции, который пронизывает эту площадь. Значит,   (1)  т. е. работа по перемещению проводника с током в магнитном поле равна произведению силы тока на магнитный поток, пересеченный движущимся проводником. Данная формула справедлива и для произвольного направления вектора В.  Рассчитаем работу по перемещению замкнутого контура с постоянным током I в магнитном поле. Будем считать, что контур М перемещается в плоскости чертежа и в результате бесконечно малого перемещения перейдет в положение М', изображенное на рис. 2 штриховой линией. Направление тока в контуре (по часовой стрелке) и магнитного поля (перпендикулярно плоскости чертежа — за чертеж или от нас) дано на рисунке. Контур М условно разобьем на два соединенных своими концами проводника: AВС и CDА.  Работа dA, которая совершается силами Ампера при иссследуемом перемещении контура в магнитном поле, равна алгебраической сумме работ по перемещению проводников AВС (dA1) и CDA (dA2), т. е.   (2)  Силы, которые приложенны к участку CDA контура, образуют острые углы с направлением перемещения, поэтому совершаемая ими работа dA2>0. .Используя (1), находим, эта работа равна произведению силы тока I в нашем контуре на пересеченный проводником CDA магнитный поток. Проводник CDA пересекает при своем движении поток dФ0 сквозь поверхность, выполненную в цвете, и поток dФ2, который пронизывает контур в его конечном положении. Значит,   (3)  Силы, которые действуют на участок AВС контура, образуют тупые углы с направлением перемещения, значит совершаемая ими работа dA1<0. Проводник AВС пересекает при своем движении поток dФ0 сквозь поверхность, выполненную в цвете, и поток dФ1, который пронизывает контур в начальном положении. Значит,   (4)  Подставляя (3) и (4) в (2), найдем выражение для элементарной работы:    где dФ2—dФ1=dФ' — изменение магнитного потока сквозь площадь, которая ограничена контуром с током. Таким образом,   (5)  Проинтегрировав выражение (5), найдем работу, которая совершается силами Ампера, при конечном произвольном перемещении контура в магнитном поле:   (6)  значит, работа по перемещению замкнутого контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока, сцепленного с контуром. Выражение (6) верно для контура любой формы в произвольном магнитном поле.

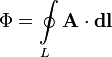
Электромагнитная индукция — явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него.

Электромагнитная индукция была открыта Майклом Фарадеем 29 августа 1831 года. Он обнаружил, что электродвижущая сила, возникающая в замкнутом проводящем контуре, пропорциональна скорости изменения магнитного потока через поверхность, ограниченную этим контуром. Величина электродвижущей силы (ЭДС) не зависит от того, что является причиной изменения потока — изменение самого магнитного поля или движение контура (или его части) в магнитном поле. Электрический ток, вызванный этой ЭДС, называется индукционным током.