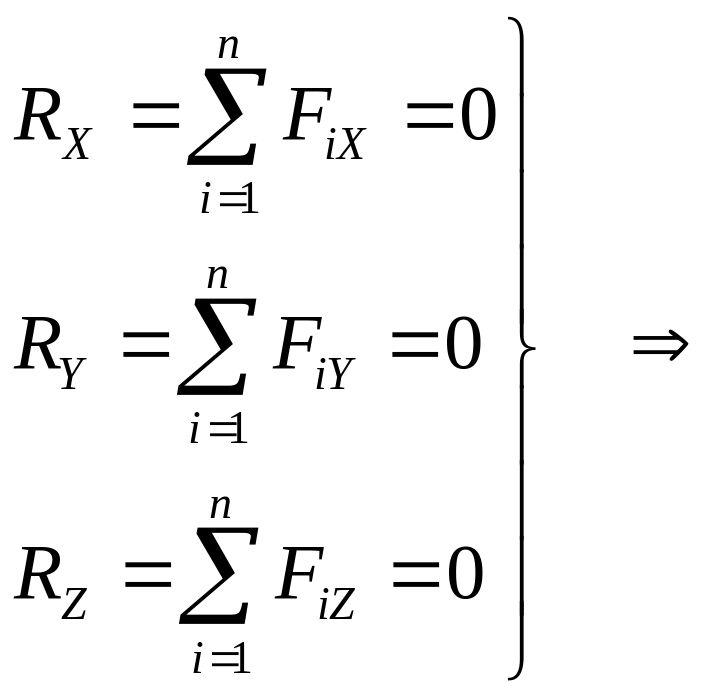- •Питання до державного екзамену з дисципліни “Теоретична механіка”
- •Методичні рекомендації щодо підготовки до державного екзамену з дисципліни “Теоретична механіка”
- •Одиниця вимірювання моменту сили – Ньютонметр, .
- •Головний момент системи сил відносно осі – момент, що дорівнює алгебраїчній сумі моментів усіх сил системи відносно осі .
Одиниця вимірювання моменту сили – Ньютонметр, .
|
|
Властивості моменту сили:
момент сили відносно центра не змінюється при переносі точки прикладання сили вздовж її лінії дії;
момент сили відносно центра О дорівнює нулю, коли:
сила дорівнює нулю (
 );
);лінія дії сили проходить через задану точку, а плече цієї сили дорівнює нулю (
 ;
;
 ).
).

Момент сили відносно точки вважатимемо: |
||
додатним, якщо сила обертатиме тіло відносно цієї точки за рухом годинникової стрілки. |
від’ємним, якщо сила обертатиме тіло відносно цієї точки проти руху годинникової стрілки. |
|
|
|
|
|
Значення і напрям моменту сили відносно точки залежить від положення точки, відносно якої визначається момент:
|
|
Модуль і напрям моменту сили відносно центру визначаємо таким чином:
 ,
,
де
![]() – проекції моменту сили
– проекції моменту сили
![]() на осі координат.
на осі координат.
Головний момент системи сил відносно центра О – момент, що дорівнює геометричній сумі моментів усіх сил системи відносно центра О.
Момент сили відносно осі
Момент
сили
відносно осі
|
|
![]() –
момент
сили
відносно осі
;
–
момент
сили
відносно осі
;
![]() – кут між вектором
і віссю
.
– кут між вектором
і віссю
.
Проекції моменту на осі координат:
 Проекції
моменту
на
осі координат
Проекції
моменту
на
осі координат
Момент сили відносно осі вважатимемо:
додатним, якщо при погляді з додатного кінця осі сила намагається обертати тіло відносно цієї осі проти руху годинникової стрілки. |
від’ємним, якщо при погляді з додатного кінця осі сила намагається обертати тіло відносно цієї осі за годинниковою стрілкою. |
|
|
Момент сили відносно осі дорівнює нулю, якщо:
лінія дії сили паралельна до осі (
 );
);лінія дії сили перетинає вісь (
 ).
).
Головний момент системи сил відносно осі – момент, що дорівнює алгебраїчній сумі моментів усіх сил системи відносно осі .
Система збіжних сил, момент рівнодійної системи збіжних сил (основні поняття, приведення системи збіжних сил до рівнодійної, умови рівноваги просторової та площинної системи збіжних сил).
Основні поняття
Система сил – сукупність кількох сил, прикладених до тіла, точки або системи точок і тіл.
Плоска система сил – система сил, лінії дії яких лежать в одній площині.
Збіжна система сил – система сил, лінії дії яких перетинаються в одній точці.
Система сил, лінії дії яких лежать в одній площині та перетинаються в одній точці, називається плоскою системою збіжних сил.
|
|
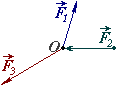
Якщо сили збіжної системи прикладені до різних точок тіла (рис. а), то згідно з наслідком 1 аксіоми 2 кожну силу можна перенести в т. О (рис. б).
а |
б |
Приведення системи збіжних сил до рівнодійної
І спосіб: Геометричне визначення рівнодійної системи збіжних сил
Рівнодійна
системи збіжних сил (![]() )
– це векторна (геометрична) сума сил
системи, що визначається за допомогою
силового багатокутника.
)
– це векторна (геометрична) сума сил
системи, що визначається за допомогою
силового багатокутника.
Силовий
багатокутник будується таким чином:
послідовно приєднують до першої сили
![]() вектор, геометрично рівний вектору
другої сили
вектор, геометрично рівний вектору
другої сили
![]() ,
і т.д. Вектор, проведений з точки
прикладання першої сили в останню
вершину побудованого багатокутника, є
рівнодійною
.
,
і т.д. Вектор, проведений з точки
прикладання першої сили в останню
вершину побудованого багатокутника, є
рівнодійною
.
|
|
|
Якщо остання вершина силового багатокутника співпадає з точкою прикладання першої сили, то багатокутник – замкнений.
|
|
|
ІІ спосіб: Аналітичне визначення рівнодійної системи збіжних сил
 ,
,
де
![]() – проекції сил
на осі координат.
– проекції сил
на осі координат.
|
Модуль рівнодійної |
Напрямні косинуси |
Для плоскої системи збіжних сил |
|
|
Для просторової системи збіжних сил |
|
|
Напрямні
косинуси
– косинуси кутів
![]() між напрямом вектора
і
додатними напрямами відповідних осей
координат.
між напрямом вектора
і
додатними напрямами відповідних осей
координат.
Умови рівноваги системи збіжних сил
Векторна (геометрична) умова рівноваги системи збіжних сил.
Для
рівноваги системи збіжних сил необхідно
і достатньо, щоб багатокутник сил
![]() був замкнений.
був замкнений.
![]()
Аналітична умова рівноваги системи збіжних сил.
|
Для
рівноваги плоскої системи збіжних
сил, які лежать в площині, наприклад
|
|
Для рівноваги просторової системи збіжних сил необхідно і достатньо, щоб алгебраїчні суми проекцій сил на три взаємно перпендикулярні осі дорівнювали нулю. |

 а
а б
б







 а
а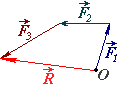 б
б а
а б
б