2.4. Объясненная и необъясненная дисперсия зависимой переменной. Коэффициент r2, его связь с коэффициентом корреляции

Цель регрессионного анализа состоит в объяснении поведения зависимой переменной у. В любой данной выборке у оказывается сравнительно низким в одних наблюдениях и сравнительно высоким - в других. Мы хотим знать, почему это так. Разброс значений у в любой выборке можно суммарно описать с помощью выборочной дисперсии Var(у). Мы должны уметь рассчитывать величину этой дисперсии.

В парном регрессионном анализе мы пытаемся объяснить поведение у путем определения регрессионной зависимости у от соответственно выбранной независимой переменной х. После построения уравнения регрессии мы можем разбить значение в каждом наблюдении на две составляющих — и :

(2.23)

Величина - расчетное значение у в наблюдении i - это то значение, которое имел бы у при условии, что уравнение регрессии было правильным, и отсутствии случайного фактора. Это, иными словами величина у, спрогнозированная по значению х в данном наблюдении.

Тогда остаток есть расхождение между фактическим и спрогнозированным значениями величины . Это та часть , которую мы не можем объяснить с помощью уравнения регрессии. Используя (2.23), разложим дисперсию :

Далее оказывается, что должна быть равна нулю, что можно доказать, используя равенство и ковариационные правила. Следовательно, мы получаем:

(2.23а)

Это означает, что мы можем разложить на две части: - часть, которая "объясняется" уравнением регрессии в вышеописанном смысле, и - "необъясненную" часть.

Другими словами, объясненная дисперсия зависимой переменной - выборочная дисперсия расчетных значений величины : ;

необъясненная дисперсия зависимой переменной - выборочная дисперсия остатков в наблюдениях: .

Выборочная дисперсия зависимой переменной регрессии равна сумме объясненной дисперсии зависимой переменной и необъясненной дисперсии зависимой переменной.

Согласно 2.23а, - это часть дисперсии , объясненная уравнением регрессии. Это отношение известно как коэффициент детерминации, и его обычно обозначают :

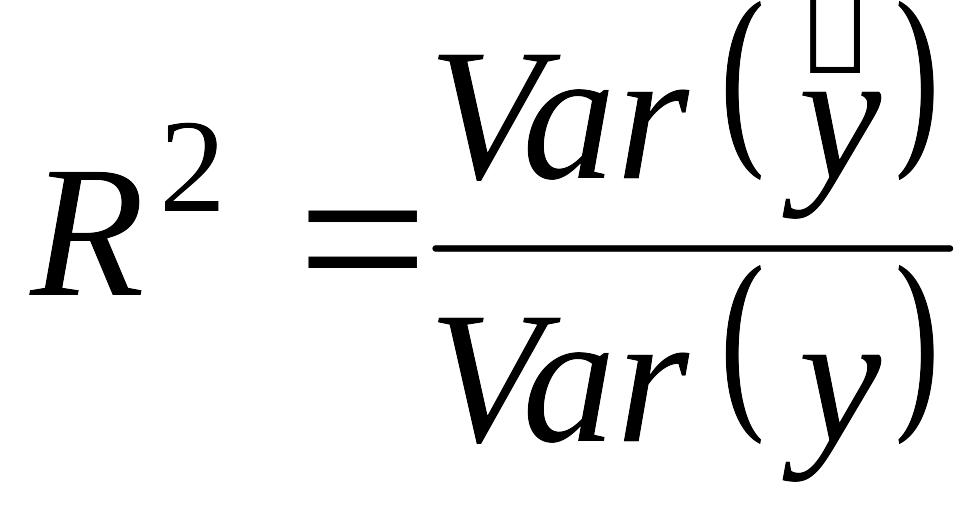, (2.24)

что равносильно

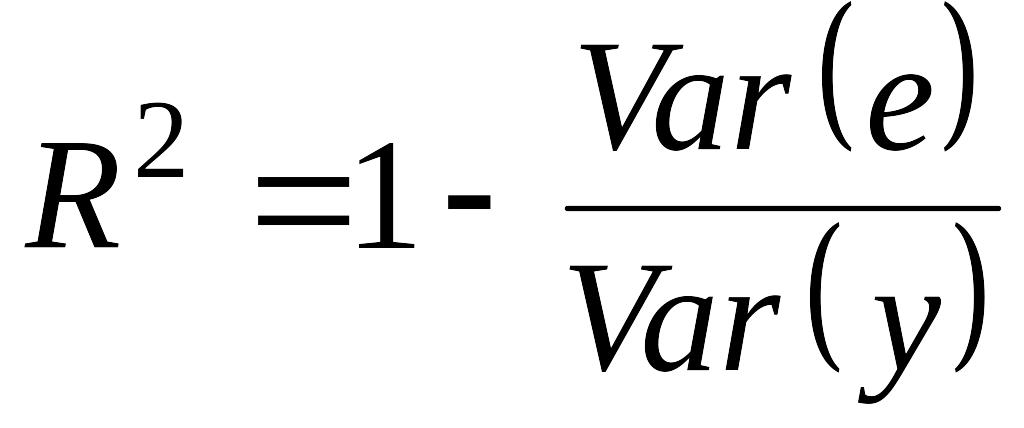, (2.25)

Часто коэффициент детерминации иллюстрируют рис.2.7.

Рис. 2.7 Соотношение TSS, ESSv\ RSS

Общая сумма квадратов отклонений (TSS - Total Sum of Squares) - сумма квадратов отклонений величины от своего выборочного среднего .

Объясненная сумма квадратов отклонений (ESS - Explained Sum of Squares) - сумма квадратов отклонений величины от своего выборочного среднего .

Необъясненная (остаточная) сумма квадратов отклонений (RSS - Residue Sum of Squares) - сумма квадратов остатков всех наблюдений.

Таким образом, коэффициент детерминации - доля объясненной дисперсии зависимой переменной во всей выборочной дисперсии :

.

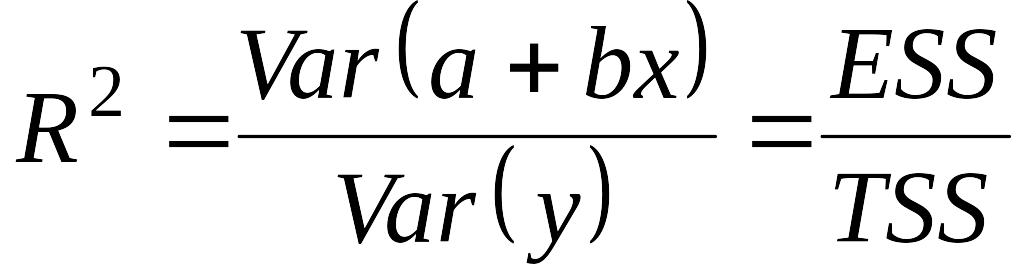Отметим также, что общая сумма квадратов отклонений равна объясненной сумме квадратов отклонений плюс необъясненная сумма квадратов отклонений: .

Из рисунка видно, что с увеличением объясненной доли разброса коэффициент приближается к единице. Кроме того, из рисунка видно, что с добавлением еще одной переменной обычно увеличивается, однако если объясняющие переменные и сильно коррелируют между собой, то они объясняют одну и ту же часть разброса переменной , и в этом случае трудно идентифицировать вклад каждой из переменных в объяснение поведения .

На интуитивном уровне представляется очевидным, что чем больше соответствие, обеспечиваемое уравнением регрессии, тем больше должен быть коэффициент корреляции для фактических и прогнозных значений , и наоборот. Покажем, что фактически равен квадрату такого коэффициента корреляции между и , который мы обозначим (заметим, что ).

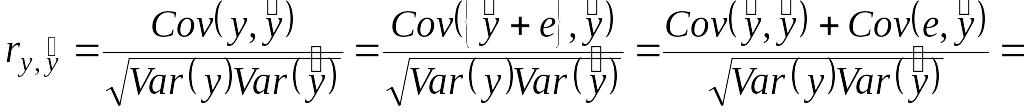
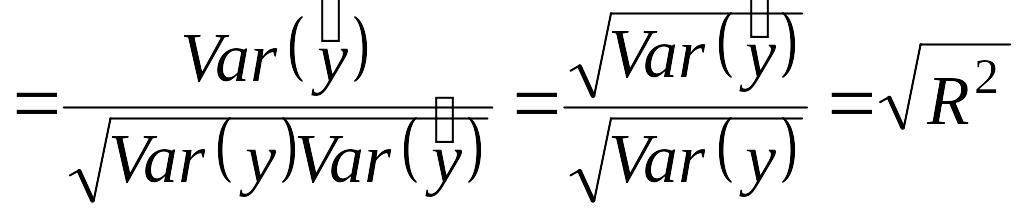. (2.26)

То есть коэффициент детерминации равен квадрату выборочной корреляции между и :

, поэтому .

Коэффициент детерминации для модели парной регрессии равен 1, только если все наблюдения лежат на одной прямой - линии регрессии.

Если в выборке отсутствует видимая связь между и , то коэффициент будет близок к нулю.

При прочих равных условиях желательно, чтобы коэффициент был как можно больше. В частности, мы заинтересованы в таком выборе коэффициентов и , чтобы максимизировать . Не противоречит ли это нашему критерию, в соответствии с которым и должны быть выбраны таким образом, чтобы минимизировать сумму квадратов остатков? Нет, легко показать, что эти критерии эквиваленты, если (2.25) используется как определение коэффициента . Отметим сначала, что

,

откуда, беря среднее значение по выборке и используя уравнение (2.9), получим:

. (2.27)

Следовательно,

. (2.28)

Отсюда следует, что принцип минимизации суммы квадратов остатков эквивалентен минимизации дисперсии остатков при условии выполнения (2.8). Однако если мы минимизируем , то при этом в соответствии с (2.29) автоматически максимизируется коэффициент .

Тем самым МНК автоматически дает максимальное возможное для данной выборки значение коэффициента детерминации .

Вычисление коэффициента выполняется на компьютере в рамках программы оценивания регрессии, поэтому данный пример приведен лишь в целях иллюстрации. Будем использовать простейший пример с тремя наблюдениями, описанный в разделе 2.3, где уравнение регрессии

(2.29)

Построения по наблюдениям и приведены в табл. 2.1. В таблице также даны и для каждого наблюдения, вычисленные с помощью уравнения регрессии (2.29), и все остальные данные, необходимые для вычисления , и . Заметим, что должно быть равно нулю, так что величина .

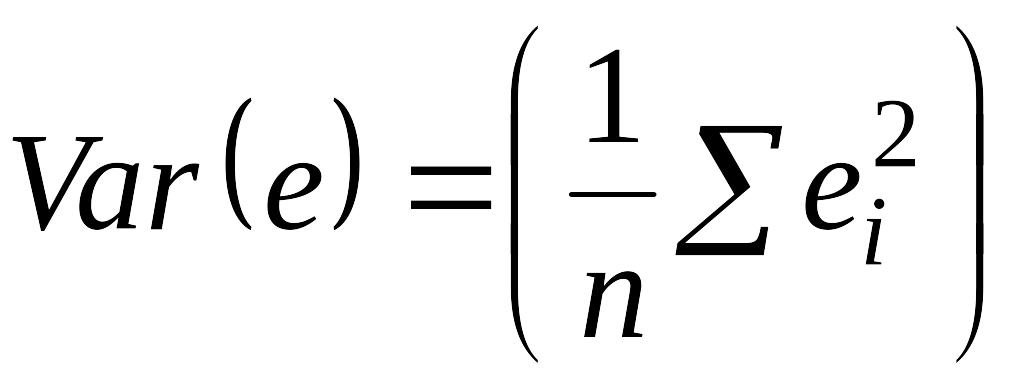Таблица 2.1