3.2. Стандартные отклонения и стандартные ошибки коэффициентов регрессии

На основании уравнения (3.20) можно показать, что b будет несмещенной оценкой , если выполняется 4-е условие Гаусса - Маркова:

(3.21)

так как - константа. Если мы примем сильную форму 4-го условия Гаусса - Маркова и предположим, что х - неслучайная величина, мы можем также считать Var(x) известной константой и, таким образом,

(3.22)

Далее, если х - неслучайная величина, то M{Cov(x,u)} = 0 и, следовательно, M{b} =

Таким образом, - несмещенная оценка Можно получить тот же результат со слабой формой 4-го условия Гаусса - Маркова (которая допускает, что переменная х имеет случайную ошибку, но предполагает, что она распределена независимо от u ).

За исключением того случая, когда случайные факторы в n наблюдениях в точности "гасят" друг друга, что может произойти лишь при случайном совпадении, b будет отличаться от в каждом конкретном эксперименте. Не будет систематической ошибки, завышающей или занижающей оценку. То же самое справедливо и для коэффициента а.

Используем уравнение (2.15):

(3.23)

Следовательно,

(3.24)

Поскольку у определяется уравнением (3.1),

(3.25)

так как M{u}=0, если выполнено 1-е условие Гаусса - Маркова. Следовательно

(3.26)

Подставив это выражение в (3.24) и воспользовавшись тем, что получим:

(3.27)

Таким образом, а - это несмещенная оценка а при условии выполнения 1-го и 4-го условий Гаусса - Маркова. Безусловно, для любой конкретной выборки фактор случайности приведет к расхождению оценки и истинного значения.

Рассмотрим теперь теоретические дисперсии оценок а и Ь. Они задаются следующими выражениями (доказательства для эквивалентных выражений можно найти в работе Дж. Томаса [Thomas, 1983, section 833]):

(3.28)

Из уравнения 3.28 можно сделать три очевидных заключения. Во-первых, дисперсии а и b прямо пропорциональны дисперсии остаточного члена .

Чем больше фактор случайности, тем хуже будут оценки при прочих равных условиях. Это уже было проиллюстрировано в экспериментах по методу Монте-Карло. Оценки в серии II были гораздо более неточными, чем в серии I, и это произошло потому, что в каждой выборке мы удвоили случайный член. Удвоив u, мы удвоили его стандартное отклонение и, следовательно, удвоили стандартные отклонения a и b. Во вторых, чем больше число наблюдений, тем меньше дисперсионных оценок. Это также имеет определенный смысл. Чем большей информацией вы располагаете, тем более точными, вероятно, будут ваши оценки. В третьих, чем больше дисперсия , тем меньше будет дисперсия коэффициентов регрессии. В чем причина этого? Напомним, что (I) коэффициенты регрессии вычисляются на основании предположения, что наблюдаемые изменения происходят вследствие изменений , но (2) в действительности они лишь отчасти вызваны изменениями , а отчасти вариациями u. Чем меньше дисперсия , тем больше, вероятно, будет относительное влияние фактора случайности при определении отклонений и тем более вероятно, что регрессионный анализ может оказаться неверным. В действительности, как видно из уравнения (3.28), важное значение имеет не абсолютная, а относительная величина и Var(x).

На практике мы не можем вычислить теоретические дисперсии или , так как неизвестно, однако мы можем получить оценку на основе остатков. Очевидно, что разброс остатков относительно линии регрессии будет отражать неизвестный разброс u относительно линии , хотя в общем остаток и случайный член в любом данном наблюдении не равны друг другу. Следовательно, выборочная дисперсия остатков Var(е), которую мы можем измерить, сможет быть использована для оценки , которую мы получить не можем.

Прежде чем пойти дальше, задайте себе следующий вопрос: какая прямая будет ближе к точкам, представляющим собой выборку наблюдений по и , истинная прямая или линия регрессии ? Ответ будет таков: линия регрессии, потому что по определению она строится таким образом, чтобы свести к минимуму сумму квадратов расстояний между ней и значениями наблюдений. Следовательно, разброс остатков у нее меньше, чем разброс значений u, и Var(e) имеет тенденцию занижать оценку . Действительно, можно показать, что математическое ожидание Var(e), если имеется всего одна независимая переменная, равно . Однако отсюда следует, что если определить как

, (3.29)

То будет представлять собой несмещенную оценку .

Таким образом, несмещенной оценкой параметра регрессии является оценка

. (3.30)

Теперь вспомним следующие определения:

стандартное отклонение случайной величины – корень квадратный из теоретической дисперсии случайной величины; среднее ожидаемое расстояние между наблюдениями этой случайной величины и ее математическим ожиданием,

стандартная ошибка случайной величины – оценка стандартного отклонения случайной величины, полученная по данным выборки.

Используя уравнения (3.28) и (3.29), можно получить оценки теоретических дисперсий для a и b и после извлечения квадратного корня – оценки их стандартных отклонений. Вместо слишком громоздкого термина «оценка стандартного отклонения функции плотности вероятости» коэффицинта регрессии будем использовать термин «стандартная ошибка» коэффициента регрессии, которую в дальнейшем мы будем обозначать в виде сокрашения «с.о.». Таким образом, для парного регрессионного анализа мы имеем:

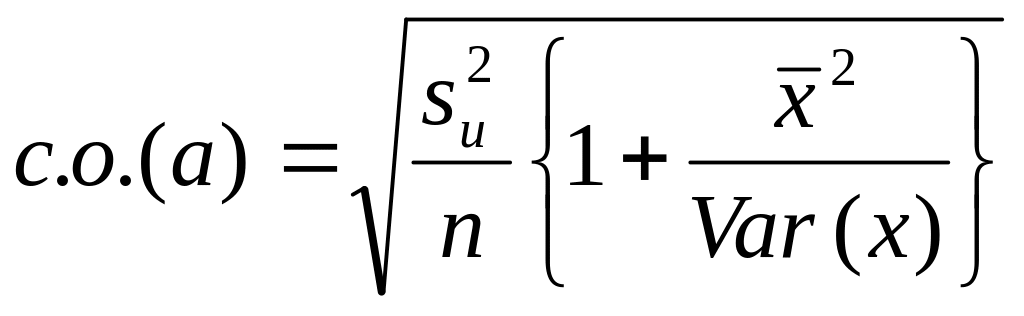и 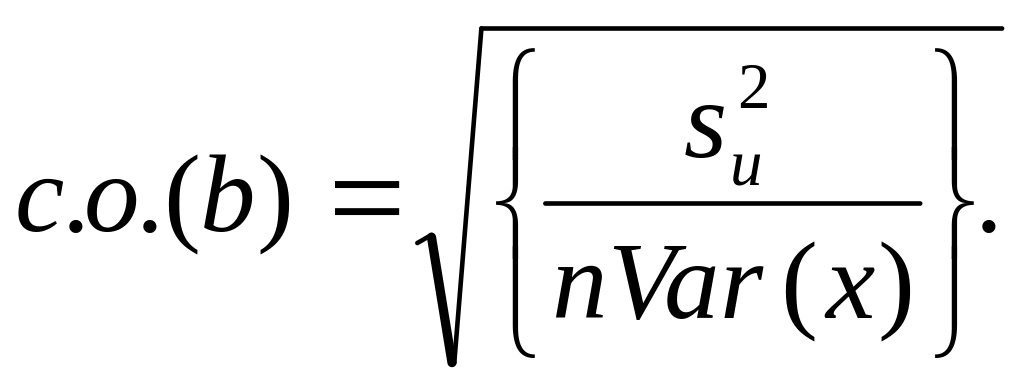(3.31)

Если воспользоваться компьютерной программой оценивания регрессии, то стандартные ошибки будут подсчитаны автоматически одновременно с оценками a и b.

Подводя итог сказанному о точности коэффициентов регрессии, акценктируем внимание на следующих выводах.

1. Оценка a для параметра имеет нормальное распределение с математическим ожиданием a и стандартным отклонением , оценка b для параметра имеет нормальное распределение с математическим ожиданием b и стандартным отклонением .

2. Для улучшения точности оценок по МНК можно увеличивать количество наблюдений в выборке n, увеличивать диапазон наблюдений Var(x) или уменьшать , (например, увеличивать точность измерений).

3. Стандартная ошибка оценки a считается по формуле

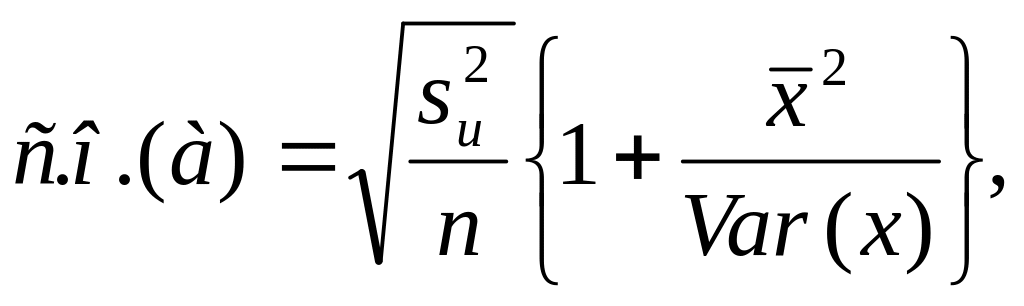
а стандартная ошибка оценки b считается по формуле . В компьютерных программах именно эти числа приводятся в круглых скобках под значениями оценок.

Полученные соотношения проиллюстрируем экспериментами по методу Монте-Карло, описанными ранее. В серии I u определялось на основе случайных чисел, взятых из генеральной совокупности с нулевым средним и единичной дисперсией а x представлял собой набор чисел от 1 до 20. Можно легко вычислить Var(x), которая равна 33,25.

Следовательно,

(3.32)

. (3.33)

Таким образом, истинное стандартное отклонение для b равно . Какие же результаты получены вместо этого компьютером в 10 экспериментах серии I? Он должен был вычислить стандартную ошибку, используя уравнение (3.31). Результаты этих расчетов для 10 экспериментов представлены в табл. 3.5.

Таблица 3.5