8. Средние значения динамических переменных

Мы уже видели, что теория отказывается предсказывать, что мы получим в результате измерения той или иной величины, она предсказывает лишь вероятности того, что будет получено то или иное значение. В связи вот с этим вероятностным характером возникает вопрос, каково среднее значение переменной? Ответ на это простой. Пусть мы имеет какую-то переменную A, и этой переменной соответствует оператор , тогда среднее значение переменнойAв состоянии (угловыми скобками будем обозначать) будет определяться так:

.

Откуда берётся такой результат? Пусть , т.е. – собственные векторы оператора , аa_n– соответствующие собственные значения. Вектор можно представить в виде разложения по собственным векторам оператора : . Тогда

=

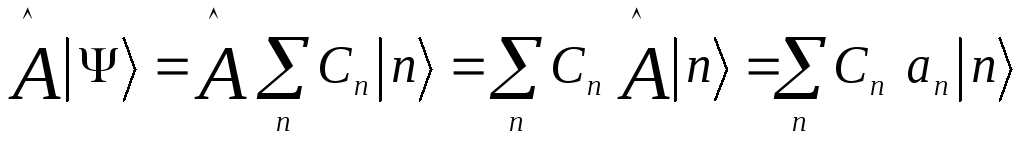
а – это вероятность получить при измерении переменнойAв состоянии значениеa_n. Возможные значения умножаются на вероятность и суммируются по всем возможным значениям, а это то, что в математике называется математическое ожидание, это и есть среднее значение данной величины.

9. Изменение со временем

Если состояние меняется со временем, это означает, что среднее значение тоже может меняться со временем. Напишем:

(это уравнение движения, пятый постулат)

(это сопряжённое уравнение)

И это изобразится, наконец, так:

12

Будем считать, что , тогда.

Если , то.

В координатном представлении:

Связь с классической механикой

,

Где классическая механика верна? Там, где можно пренебречь соотношениями неопределённостей!

(отлична от нуля в маленькой области)

10. Атом водорода. Частица в центрально симметричном поле

Пусть , т.е. поле обладает центральной симметрией, тогда. Гамильтониан в координатном представлении имеет вид. Пишем уравнение на собственные векторы:

В полярных координатах оператор Лапласа имеет вид

,

где содержит слагаемые с производными по переменными.

Можно показать, что оператор квадрата импульса и гамильтониан коммутируют: . Физически это означает, чтоL²сохраняется. Итоже, значит операторыимеют общие собственные векторы.

Положительно заряжённое ядро создаёт поле или в более общем виде. Вектор, где,,, будет решением уравнения на собственные векторы гамильтониана, при чём

Вектору в координатном представлении отвечает функция.

Стационарное состояние электрона в атоме водорода задаётся тремя числами n,l,m, эти числа определяют энергиюE_n, момент и проекцию импульса соответствующие этому состоянию, при чём. Это вследствие того, что.

Бор постулировал, что существуют орбиты, на которых электроны не излучают и ещё

1) , гдеn– номер орбиты,

2) .

Из этих постулатов следует, что

и.

При Z= 1 (водород) иn= 1.

11. Система тождественных частиц

Пусть система состоит из Nчастиц, а её состояние задаётся векторомтогда соответственно

(вероятность обнаружить частицу в элементе объёма) =.

,

,

где .

В квантовой механике частицы одного сорта тождественны, принципиально неразличимы (рис. 11.1). Пусть у нас имеется две частицы, тогда

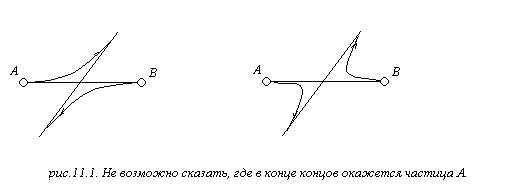
Как это может быть? Так как модуль вектора постоянен, то вектор может только вращаться вокруг начала координат:. Из условия нормировки следует:, это выполняется только в двух случаях:и. Так как, возможны две ситуации:

1. , волновая функция симметрична относительно перестановки пары тождественных частиц, такие частицы называютсябозоны;

2. , этофермионы.

Принцип Паулигласит, что два фермиона не могут находиться в одном и том же состоянии.