§3.2 Приложение элементарных цепей.

Говорим, что теория Т устойчива относительно подмножества, если всякая подмодель любой модели Т будет моделью Т. Теория Т устойчива относительно объединений цепей, если объединение всякой цепи моделей Т будет моделью Т. Теория Т устойчива относительно гомоморфизмов, если всякий образ любой ее модели будет ее моделью.

Теория	Устойчива относительно
	подмоделей		гомомрфизмов
Булевы алгебры Группы с символом –х Группы Коммутативные кольца Поля Плотный линейный порядок Области целостности Алгебраически замкнутые поля Атомные булевы алгебры Арифметика Пеано ZF	да да нет нет нет нет нет нет нет нет нет нет	да да да да да да да да нет нет нет нет	да да да да да нет нет нет да нет нет нет

24. ЛЕММА 3.1 Пусть Т – непротиворечивая теория языка , а – множество предложения языка , замкнутое относительно конечных дизъюнкций. Тогда следующие утверждения эквивалентны.

(а) Т имеет множество аксиом Г таких, что Г= .

(б) Если – модель Т, модель языка и всякое предложение , истинное в истинно в , то модель теории Т.

ДОКАЗАТЕЛЬСТВО. Ясно, что (а) (б). Пусть выполнимо (б) и Г – множество всех предложений языка , для которых и Тогда ясно . Покажем, что и , откуда следует, что множества предложения Т являются аксиомами Г. Пусть - произвольная модель для Г. Пусть . Покажем, что теория непротиворечива. Иначе найдутся такие предложения что . Поэтому . Т.к. замкнуто относительно, то а поэтому . Это противоречит тому, что .Значит непротиворечива и поэтому имеет модель . Тогда всякое предложение , истинное в должно быть истинным в , потому что в противном случае

21. ТЕОРЕМА (об устойчивости относительно подмоделей). Теория Т устойчива относительно подмоделей она обладает множеством - аксиом.

ДОКАЗАТЕЛЬСТВО. В одну сторону утверждение очевидно. Пусть Т – устойчива относительно подмоделей. Применим лемму 2.1, приняв за множество всех предложений, эквивалентных - предложениям. Рассмотрим две модели и такие, что всякое - предложение, истинное в , истинно и в . Тогда всякое - предложение, истинное в , истинно в . Рассмотрим теорию в языке , где диаграмма Теория непротиворечива т.к. для любого конечного множества - предложение истинно в , а потому и в Поэтому оно совестно с теорией Т. Пусть – модель . Модель является подмоделью , а сама очевидно, - моделью теории Т. Поэтому и - модель Т. Согласно лемме 2.1, Т имеет множество - аксиом.

22. ТЕОРЕМА (об устойчивости объединения цепей). Теория Т устойчива относительно объединения цепей Т обладает множеством - аксиом.

ДОКАЗАТЕЛЬСТВО. Пусть Г – множество - аксиом теории Т, – цепь ее моделей и . Рассмотрим из Г предложение где уже не содержит кванторов. Каждая модель для Пусть . Для некоторого имеем . Тогда существуют такие , что Значит а потому . Значит модель для Г, а потому и для Т.

Обозначим через множество всех предложений, эквивалентных - предложениям. Множество замкнуто относительно конечных дизъюнкций. Пусть - такие модели, что и всякое предложение, истинное в , истинно и в . Докажем

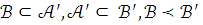1. Существуют такие модели что и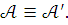

Для каждого введем по новой константе с_b, образовав модель и язык . Пусть Т₁ – полная теория модели в языке , а Т₂ – множество всех предложений , истинных в Теория непротиворечива, т.к. Т₂ замкнута (с точностью до эквивалентности) относительно конъюнкций и каково бы ни было предложение , предложение истинно в , а потому и в . Пусть – модель теории . Тогда Кроме того, всякое предложение языка истинное в истинно и в Обогатим и , добавив к нему по новой константе с_а для каждого Тогда теория (т.е. с элементарной диаграммой модели ) непротиворечива. Поэтому она имеет модель и тогда т.е (1) доказано.

Итерируя построение (1), получаем такую цепь , что для каждого n и Пусть – объединение этой цепи. Поскольку каждая из – модель Т, будет моделью для Т. Но служит объединением элементарной цепи Поэтому по теореме об элементарных цепях и, следовательно, – также модель теории Т. По лемме 2.1 заключаем, что Т имеет множество - аксиом.

Формулу назовем позитивной, если она построена из атомных с использованием только связок и кванторов .

23. ТЕОРЕМА (об устойчивости относительно гомоморфизмов). Непротиворечивая теория Т устойчива относительно гомоморфизмов она обладает множеством позитивных аксиом.

ДОКАЗАТЕЛЬСТВО. Формула называется устойчивой относительно гомоморфизмов, если для всякого гомоморфизма модели на модель и для любых элементов из условия следует, что Нужно показать, что все позитивные формулы устойчивы относительно гомоморфизмов. Утверждение верно для атомных формул и сохраняется при шаге индукции, на котором вводятся связки . Предположим, что оно верно для формулы и дано, что . Тогда для некоторого имеем и поэтому Пусть теперь дано, что и b – произвольный элемент из В. Тогда для некоторого . Теперь , и, следовательно, . Поэтому формулы и оказываются устойчивыми относительно гомоморфизмов.

Пусть выражение означает, что всякое позитичное предложение, истинное в модели , истинно и в . Сначала докажем, что

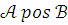1. если , то существует элементарное расширение 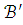модели 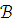и вложение такое, что .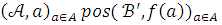

Для этого добавим к рассматриваемому языку новые константы Пусть Т₁ – множество всех позитивных предложений языка , истинных в модели , а Т₂ – множество всех позитивных предложений языка , истинных в модели . Теория непротиворечива, т.к. - модель теории . Из определения Т₂ следует, что . Пусть – вложение, определяемое равенством . Определение теории Т₁ показывает, что .

С помощью аналогичных рассуждений доказывается

2. если , то существует элементарное расшир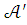ение модели и отображение такое, что .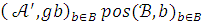

Пусть теперь и – такие модели, что и . Итерируя построения (1) и (2), получим диаграмму

удовлетворяющую условиям

и так далее. Отсюда следует, что при всяком n отображение – гомоморфизм модели в модель и , .

Обозначим через , и положим . Тогда – гомоморфизм Согласно теореме об элементарных цепях , , откуда следует, что модель теории Т, а потому . Следовательно, по лемме 2.1 теория Т обладает множеством позитивных аксиом.