
Министерство сельского хозяйства Российской Федерации
Департамент научно-технологической политики и образования
ФГОУ ВПО «Волгоградская государственная сельскохозяйственная
академия»
Кафедра высшей математики
Методические указания
для проведения практических занятий по математике по темам:
Кратные и криволинейные интегралы
для специальностей:
110301.65 - Механизация сельского хозяйства
110304.65 - Технология обслуживания и ремонта машин в апк.
050501.65 - Профессиональное обучение.

Волгоград
ИПК «Нива»
2009
УДК 517.3
ББК 22.161.1
К 67 М 54
Методические указания для проведения практических занятий по математике по темам: Кратные и криволинейные интегралы.
Сост. А.А. Шубович; Волгогр. Гос. с.-х. акад. Волгоград, 2009. 12 с.
Пособие может служить сборником задач, справочником по данным разделам высшей математики, решебником, руководством по решению задач. С его помощью можно готовиться к практическим занятиям преподавателям высшей математики, а также студентам инженерных специальностей. Решение самостоятельных индивидуальных работ также может опираться на разобранные примеры и задачи. Количество часов и построение материала полностью соответствует программе по математике на факультете механизации сельского хозяйства во втором семестре.
Для студентов инженерных специальностей.
Методические указания рекомендованы методическим советом факультета электрификации сельского хозяйства Волгоградской государственной сельскохозяйственной академией, протокол № 4 от 27 ноября 2008 года.
© А. А. Шубович, 2009
© ФГОУ ВПО «Волгоградская государственная
сельскохозяйственная академия, 2009
Практические занятия.
Второй семестр. II модуль. 7 занятий. (с 22.04 по 28.05)
Раздел 6: «Кратные и криволинейные интегралы».
7 Практических занятий (в том числе 1 контрольная работа).
1-е занятие. Вычисление двойных интегралов.
Повторить: определение, свойства, правила вычисления двойного интеграла.
1. Если область интегрирования
![]() ограничена слева и справа прямыми
ограничена слева и справа прямыми
![]() и
и
![]()
![]() ,
а снизу и сверху – непрерывными кривыми
,
а снизу и сверху – непрерывными кривыми
![]() и
и
![]() ,
каждая из которых пересекается
вертикальной прямой только в одной
точке, то
,
каждая из которых пересекается
вертикальной прямой только в одной
точке, то
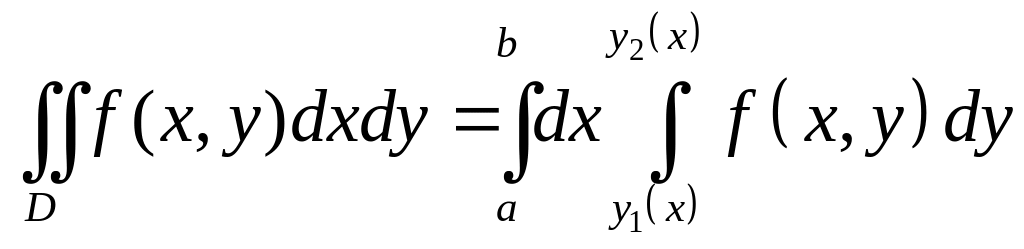 ,
,
причём сначала вычисляется внутренний
интеграл
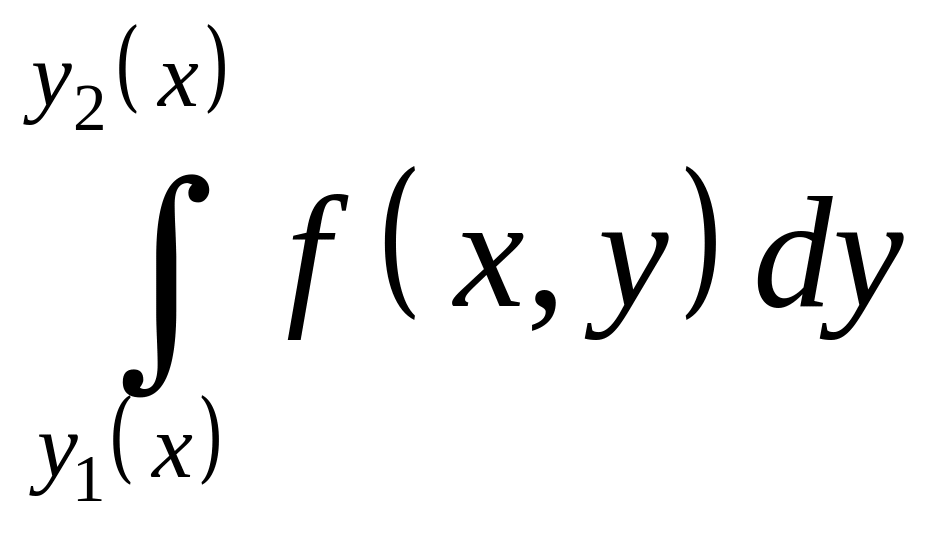 ,
в котором
,
в котором
![]() .
.
2. Если область интегрирования
ограничена снизу и сверху прямыми
![]() и
и
![]()
![]() ,
а слева и справа – непрерывными кривыми
,
а слева и справа – непрерывными кривыми
![]() и
и
![]() ,
каждая из которых пересекается
вертикальной прямой только в одной
точке, то
,
каждая из которых пересекается
вертикальной прямой только в одной
точке, то
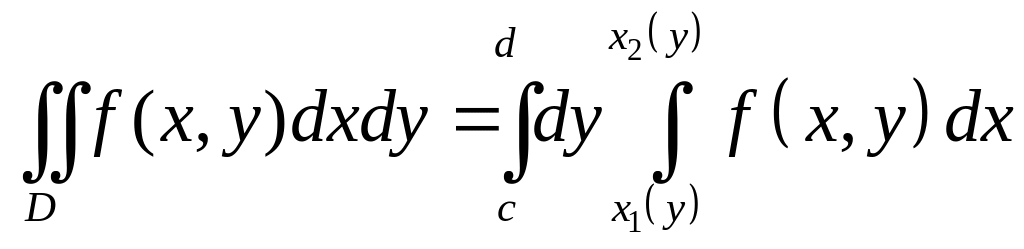 ,
,
причём сначала вычисляется внутренний
интеграл
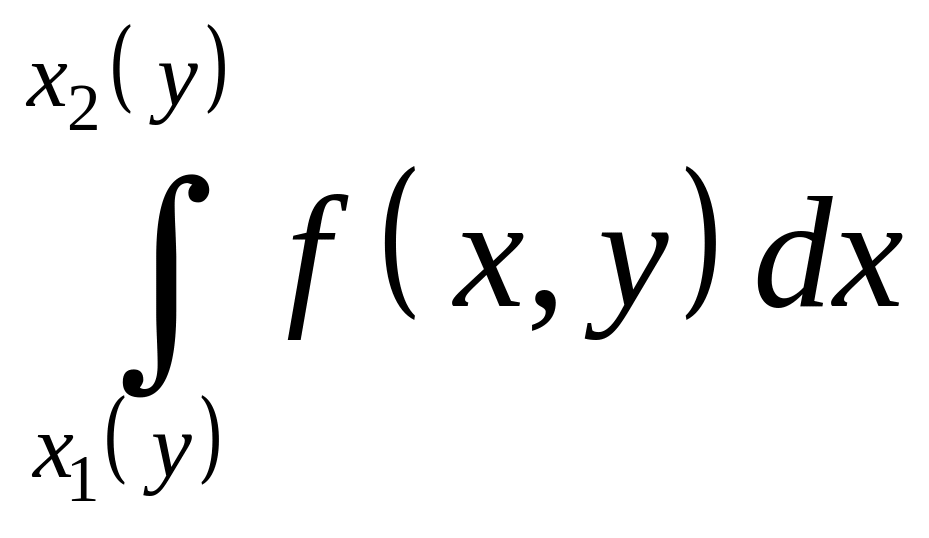 ,
в котором
,
в котором
![]() .
.
3. В общем случае, область интегрирования путём разбиения на части сводится к основным областям.
Задания для решения.
Вычислить двойной интеграл.
1).
![]() ,
если область
,
если область
![]() - прямоугольник.
- прямоугольник.
Решение.
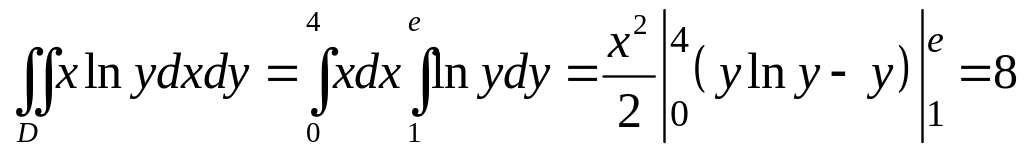 .
.
2).
![]() ,
если
,
если
![]() - квадрат. Ответ:
- квадрат. Ответ:
![]() .
Указание. Использовать формулы
.
Указание. Использовать формулы
![]() ;
;
![]() .
.
3).
![]() ,
где
,
где
![]() .
Ответ:
.
Ответ:
![]() .
.
4).
![]() ,
если
,
если
![]() .
.
Ответ:
![]() .
.
Вычислить повторный интеграл.
1).

 .
.
2).
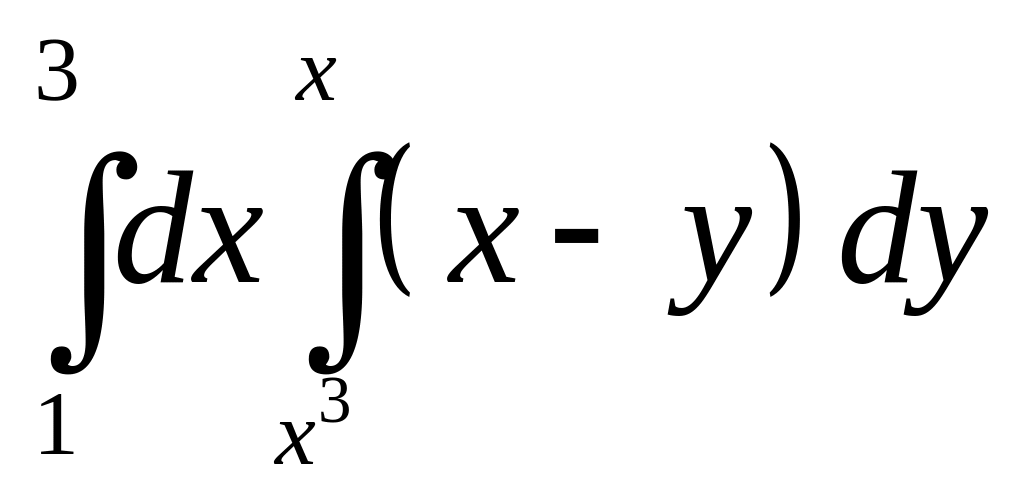 .
Ответ:
.
Ответ:
![]() .
.
Вычислить двойной интеграл по заданной области.
1).
![]() ,
если область
ограничена линиями
,
если область
ограничена линиями
![]() ,
,
![]() .
.
Р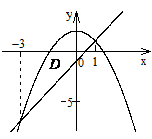 ешение.
Построим линии и определим точки их
пересечения:
ешение.
Построим линии и определим точки их
пересечения:
![]() ,
откуда
,
откуда
![]() или
или
![]() ,
тогда
,
тогда
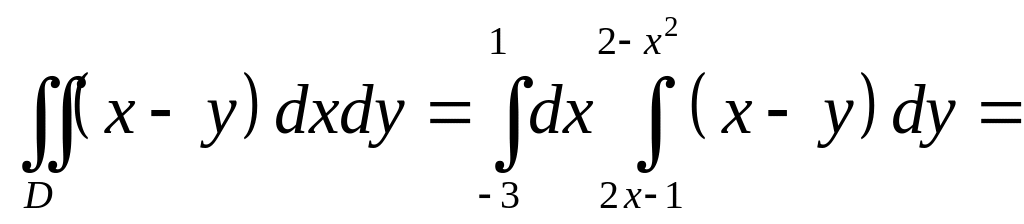
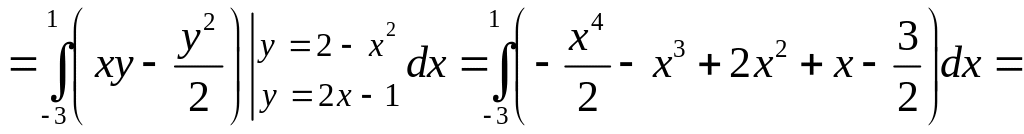
![]() .
.
2).
![]() ,
если область
ограничена линиями
,
если область
ограничена линиями
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
3).
.
3).![]() ,
если область
ограничена линиями
,
,
если область
ограничена линиями
,
![]() ,
,
![]() ,
,
![]() .
.
4).
![]() ,
если область
ограничена линиями
,
,
если область
ограничена линиями
,
![]() ,
.
,
.
5).
![]() ,
если область
ограничена линиями
,
если область
ограничена линиями
![]() ,
,
![]() ,
.
,
.
6).
![]() ,
если область
- треугольник с вершинами
,
если область
- треугольник с вершинами
![]() ,
,
![]() ,
,
![]() .
.
Ответы: 2).![]() ;
3).
;
3).
![]() ;
4).
;
4).
![]() ;
5).
;
5).
![]() ;
6).
;
6).
![]() .
.
2-е занятие. Изменение порядка интегрирования и замена переменной в двойном интеграле.
Повторить: свойства и правила вычисление двойных интегралов, полярную систему координат.
План решения первой задачи.
Изобразить область, ограниченную заданными линиями.
Определить функции, обратные к данным линиям.
Меняем порядок интегрирования, для чего заданную область представим в виде одной или объединения нескольких областей другого вида.
Записываем двойной интеграл или сумму двойных интегралов.
Задания для решения. Изменить порядок интегрирования в интегралах.
1).
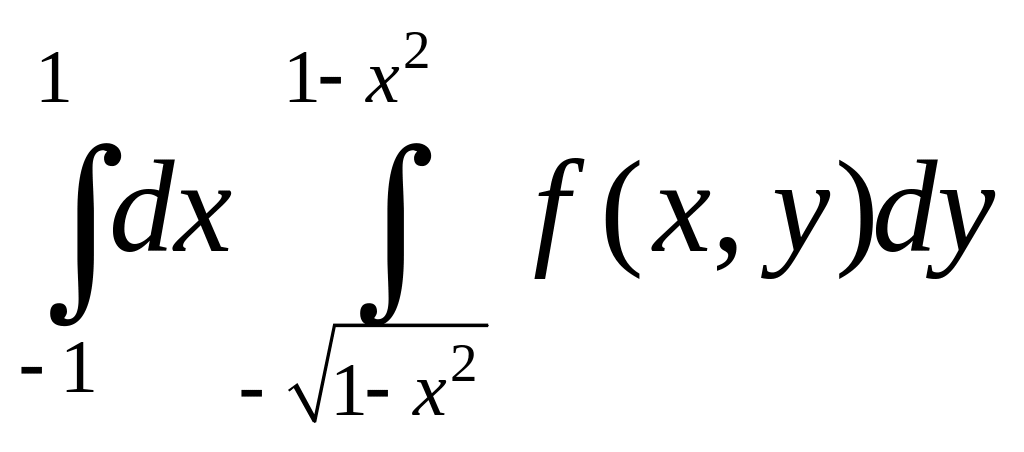 .
2).
.
2).
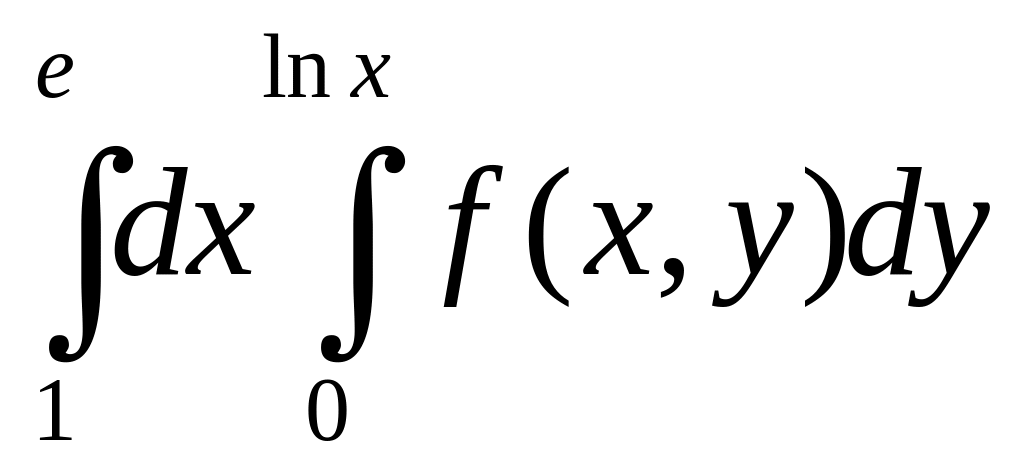 .
3).
.
3).
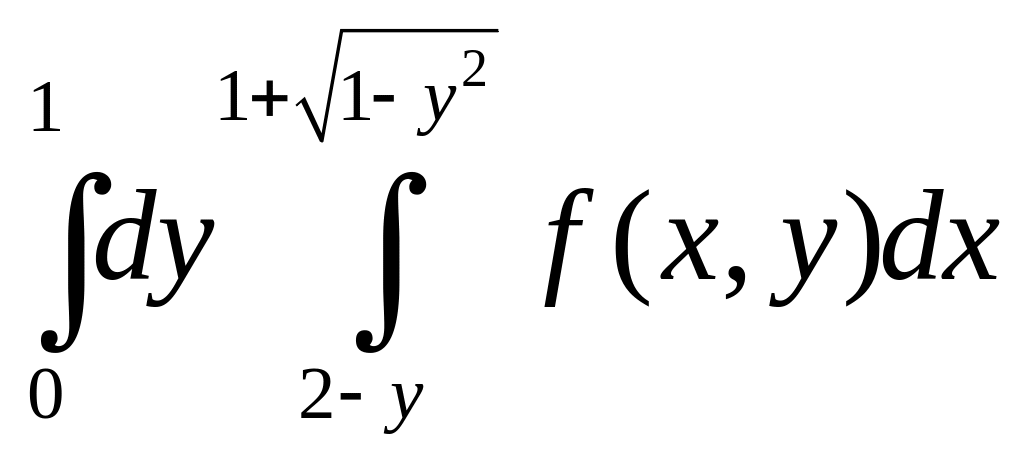 .
4).
.
4).
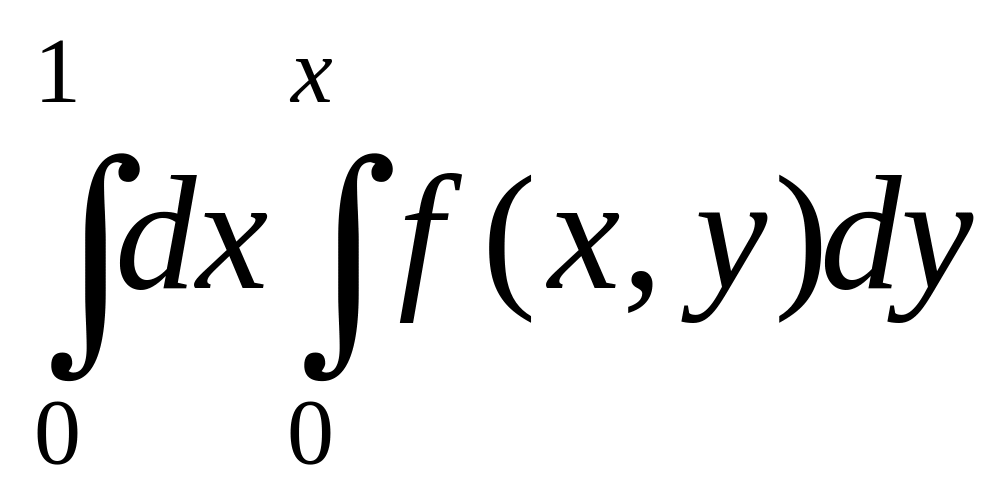 .
5).
.
5).
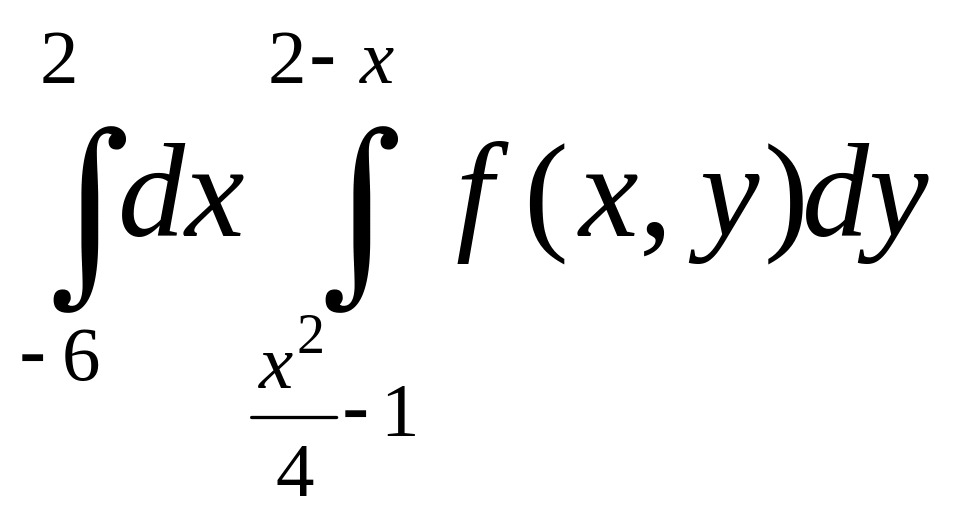 .
6).
.
6).
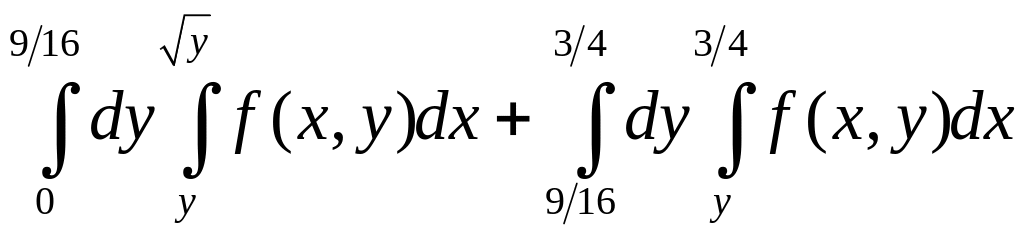 .
.
Решение. 1). Область
ограничена линиями
![]() ,
,
,
,
![]() ,
,
![]() ,
откуда
,
откуда
![]() и
и
![]() .
Изменим порядок интегрирования, для
ч
.
Изменим порядок интегрирования, для
ч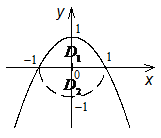 его
заданную область представим в виде двух
областей
его
заданную область представим в виде двух
областей
![]() другого
вида:
другого
вида:
![]() и
и
![]() .
Тогда
.
Тогда
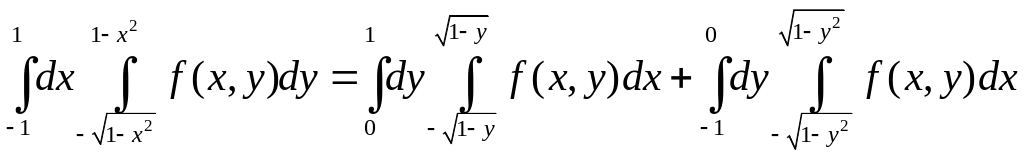 .
.
Ответы. 2).
 .
3).
.
3).
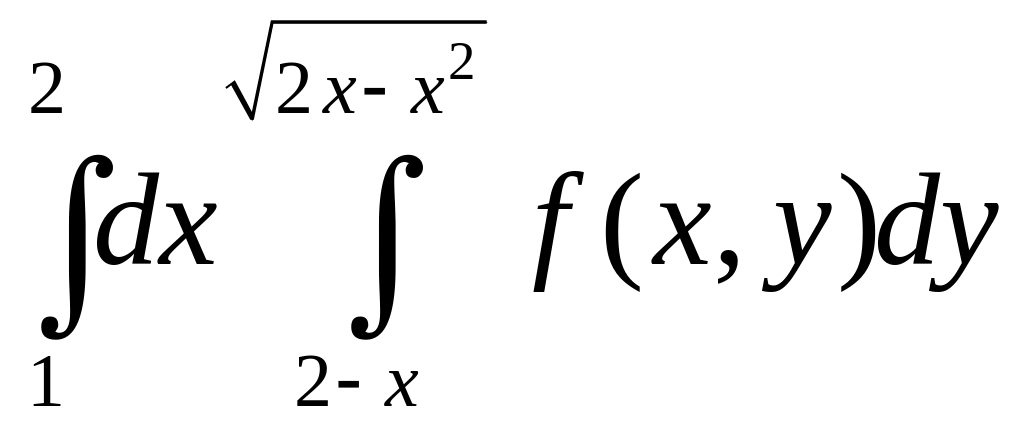 .
4).
.
4).
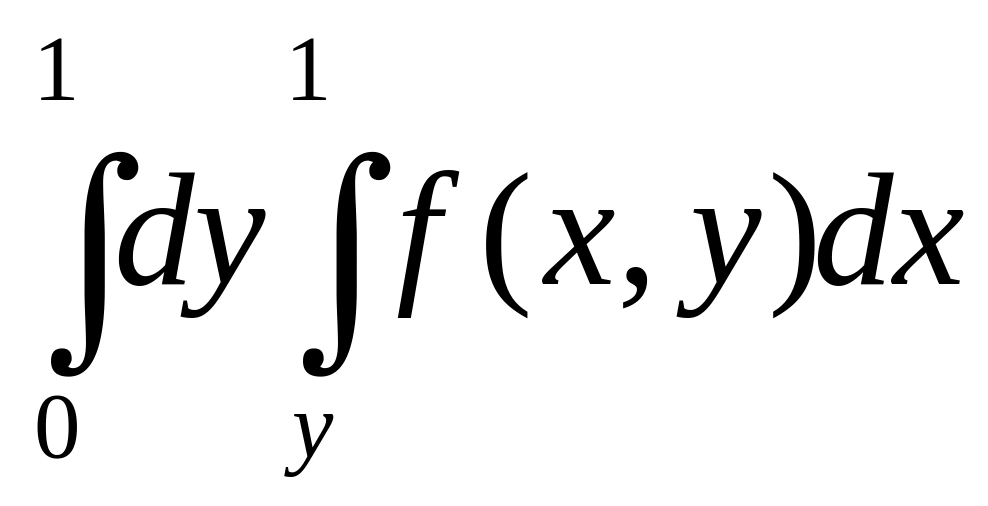 .
.
5).
 .
6).
.
6).
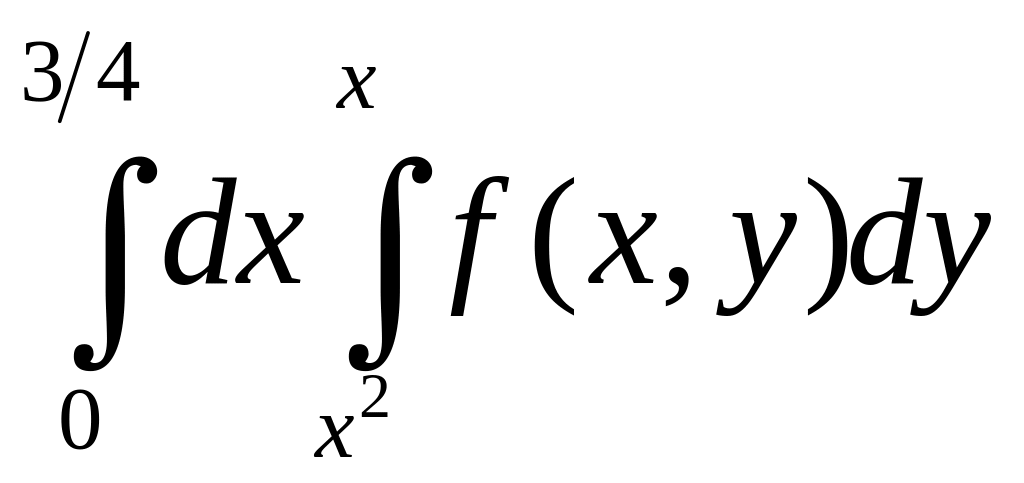 .
.
Рассмотрим частный случай замены переменной в двойном интеграле – переход к полярной системе координат. При этом
 ,
,
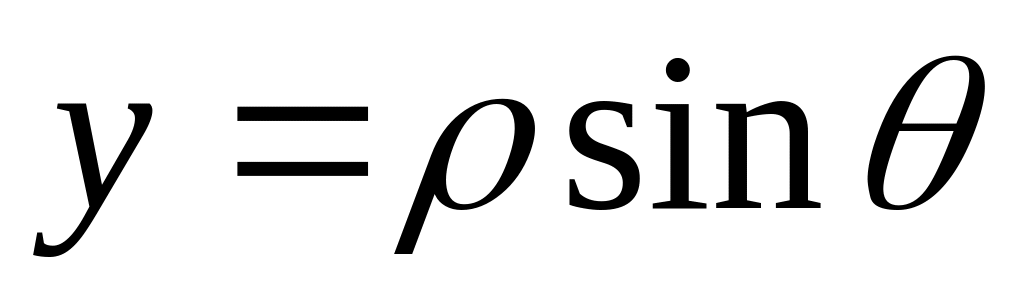 ,
якобиан перехода
,
якобиан перехода
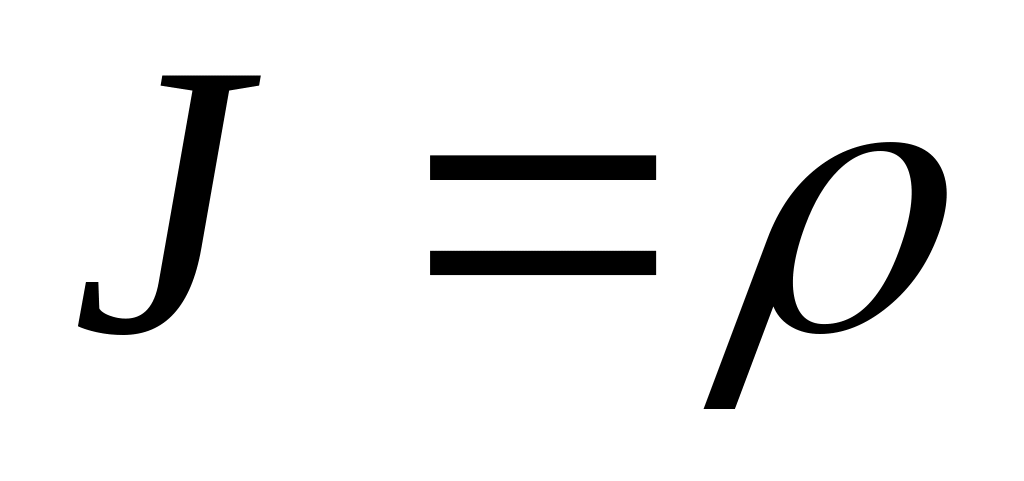 ,
тогда
,
тогда
 .
.
Задания для решения. Вычислить двойные интегралы, переходя к полярной системе координат.
1).
![]() ,
если
- I четверть круга
,
если
- I четверть круга
![]() .
.
Решение. Пусть
,
,
тогда
![]() .
В первой четверти
.
В первой четверти
![]() ,
,
![]() и
и
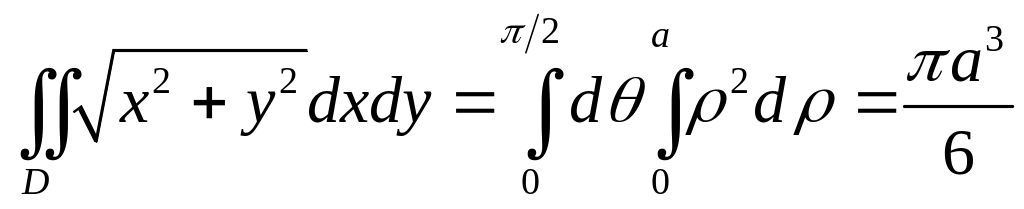 .
.
2).
![]() ,
если область
- кольцо между окружностями
,
если область
- кольцо между окружностями
![]() и
и
![]() .
Ответ:
.
Ответ:
![]() .
.
Указание. Применить формулу интегрирования по частям в определённом интеграле.
3).
![]() ,
где
ограничена полуокружностью
,
где
ограничена полуокружностью
![]() и осью
и осью
![]() .
.
Ответ:
![]() .
.
4).
,
если
- окружность
![]() .
Ответ:
.
Ответ:
![]() .
.
3-е занятие. Вычисление площади плоской фигуры.
Повторить: формулы для вычисления площади плоской фигуры в прямоугольных и полярных координатах.
1. Площадь плоской фигуры, ограниченной областью находится по формуле:
![]() .
.
2. Если
![]() ,
то
,
то
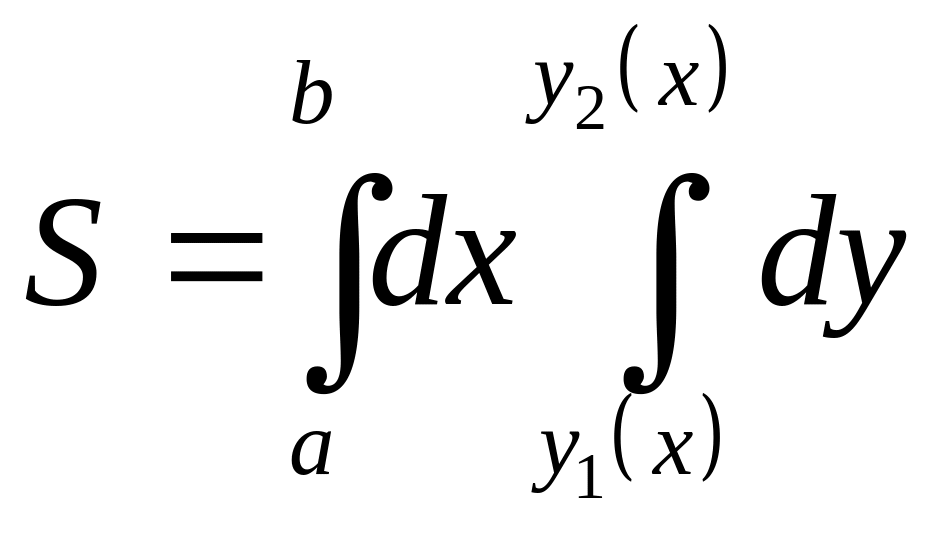 .
.
3. Если
![]() ,
то
,
то
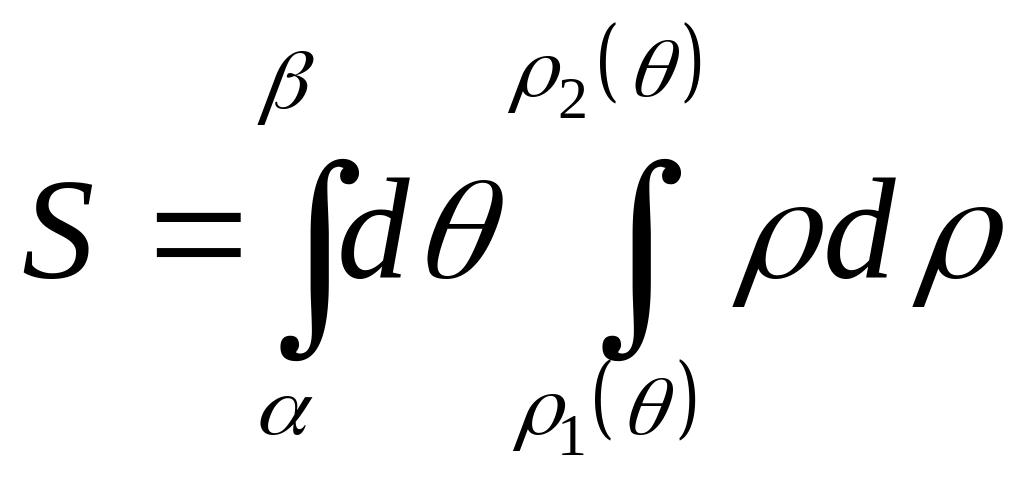 .
.
Задания для решения.
Найти площадь фигуры в прямоугольных координатах.
1). Вычислить площадь фигуры, ограниченной
линиями
![]() ,
,
![]() .
.
Р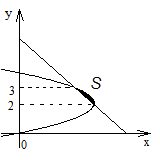 ешение.
Определим точки пересечения линий из
уравнения
ешение.
Определим точки пересечения линий из
уравнения
![]() .
Получим точки
.
Получим точки
![]() и
и
![]() .
Поэтому
.
Поэтому
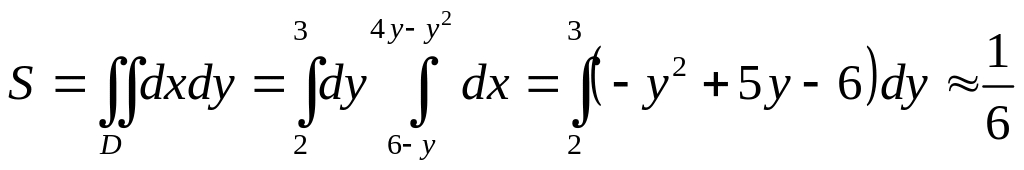 кв. ед.
кв. ед.
2).
![]() ,
,
![]() .
.
3).
![]() ,
,
![]() .
.
4).
![]() ,
,
![]() .
.
5).
![]() ,
,
![]() .
.
Ответы: 2).
![]() кв. ед. 3).
кв. ед. 3).
![]() кв. ед. 4).
кв. ед. 4).
![]() кв. ед. 5).
кв. ед. 5).
![]() кв. ед.
кв. ед.
Найти площадь фигуры в полярных координатах.
1 ).
Вычислить площадь фигуры, ограниченной
окружностями
).
Вычислить площадь фигуры, ограниченной
окружностями
![]() ,
,
![]() (вне окружности
).
(вне окружности
).
Решение. Найдём координаты точки
![]() :
:
![]() ,
,
![]() ,
,
![]() .
Значит
.
Значит
![]() ,
тогда
,
тогда

 кв. ед.
кв. ед.
2).
![]() ,
,
![]() (вне кардиоиды).
(вне кардиоиды).
3).
![]() ,
,
![]() .
.
Ответы: 2).
![]() кв. ед. 3).
кв. ед. 3).
![]() кв.ед.
кв.ед.
Найти площадь фигуры переходом к полярной системе координат.
1). Вычислить площадь, ограниченную
лемнискатой
![]() .
.
Решение. Перейдём к полярным координатам
по формулам
,
,
получим
![]() .
Фигура симметрична относительно начала
координат, поэтому изменение
.
Фигура симметрична относительно начала
координат, поэтому изменение
![]() соответствует четверти искомой площади,
значит
соответствует четверти искомой площади,
значит
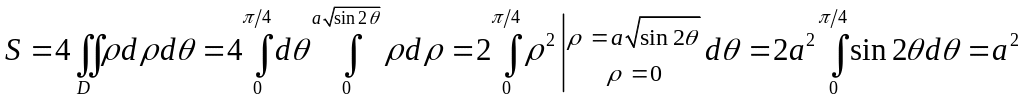 .
.
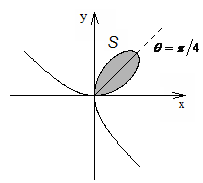
2). Найти площадь фигуры, ограниченной
линией
![]() (петля).
(петля).
Указание. Осью симметрии петли является
![]() .
В полученном интеграле сделать замену
переменной
.
В полученном интеграле сделать замену
переменной
![]() .
Ответ:
.
Ответ:
![]() .
.
4-е занятие. Вычисление тройных интегралов.
Повторить: правило вычисления тройного интеграла, цилиндрические и сферические координаты.
1. Если
![]() ,
то
,
то
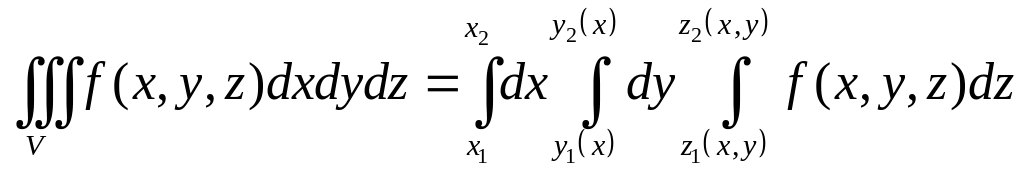 .
.
2. Цилиндрические координаты:
![]() ,
,
![]() ,
,
![]() .
При этом
.
При этом
![]() ,
,
![]() ,
,
![]() .
Якобиан преобразования
,
поэтому
.
Якобиан преобразования
,
поэтому
![]() .
.
3. Сферические координаты (их называют
полярными координатами в пространстве):
![]() ,
,
![]() ,
,
![]() .
При этом
,
,
.
При этом
,
,
![]() .
Якобиан преобразования
.
Якобиан преобразования
![]() ,
поэтому
,
поэтому
![]() .
.
Задания для решения.
Вычислить тройной интеграл по заданной области.
1).
![]() ,
где область
,
где область
![]() определяется неравенствами
определяется неравенствами
![]() ,
,
![]() ,
,
![]() .
.
Решение.
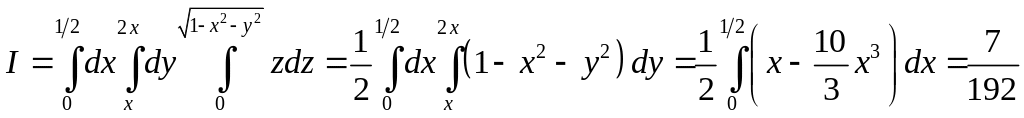 .
.
2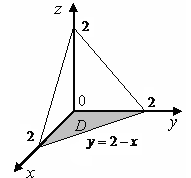 ).
).
![]() ,
если область
ограничена плоскостями
,
,
если область
ограничена плоскостями
,
![]() ,
,
![]() ,
,
![]() .
.
Решение. Область
ограничена сверху плоскостью
![]() ,
а снизу – плоскостью
.
Проекцией тела на плоскость
,
а снизу – плоскостью
.
Проекцией тела на плоскость
![]() служит область
служит область
![]() .
Следовательно,
.
Следовательно,
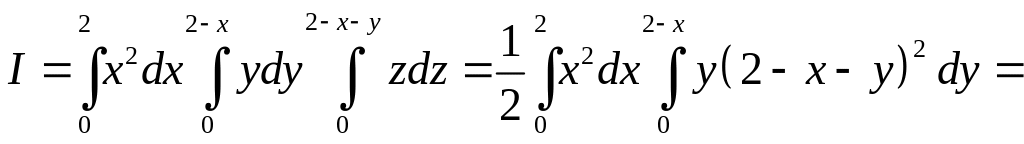

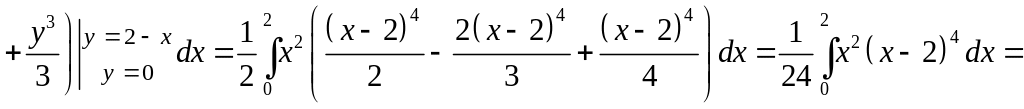
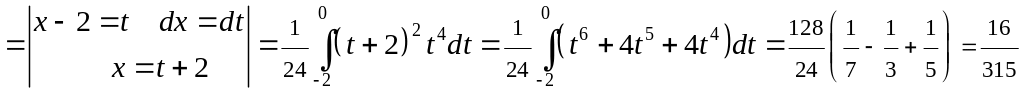 .
.
3).
![]() ,
если
- прямоугольный параллелепипед,
определяемый неравенствами
,
если
- прямоугольный параллелепипед,
определяемый неравенствами
![]() ,
,
![]() ,
,
![]() .
Ответ:
.
Ответ:
![]() .
.
4).
![]() ,
если тело
ограничено поверхностями
,
если тело
ограничено поверхностями
![]() ,
,
,
.
Ответ:
,
,
,
.
Ответ:
![]() .
.
Вычислить тройной интеграл переходом к цилиндрической или сферической системе координат.
1).
![]() ,
если
- шар
,
если
- шар
![]() .
.
Решение. Перейдём к сферическим
координатам. В области
:
![]() ,
,
,
тогда
,
,
,
тогда
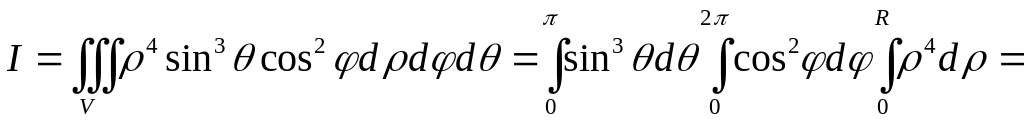
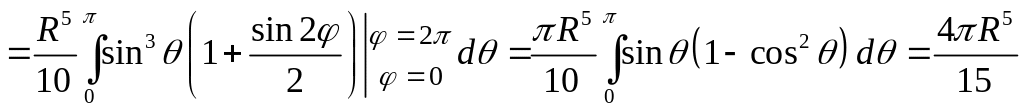 .
.
2).
![]() ,
если область
ограничена цилиндром
,
если область
ограничена цилиндром
![]() и плоскостями
,
,
и плоскостями
,
,
![]() .
.
Решение. Перейдём к цилиндрическим
координатам. Уравнение цилиндра в этих
координатах примет вид
![]() .
Следовательно, в области
:
.
Следовательно, в области
:
![]() ,
,
![]() (т. к.
(т. к.
![]() ),
),
![]() .
Поэтому
.
Поэтому

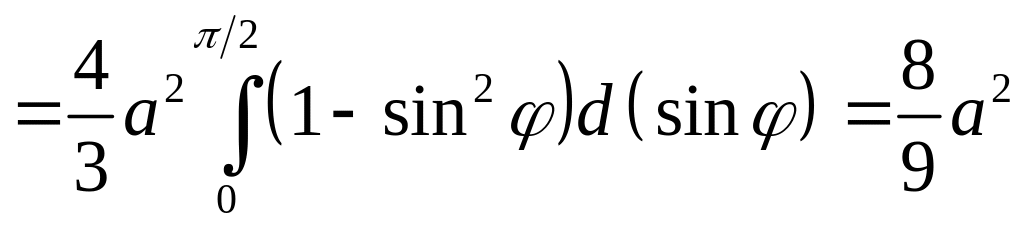 .
.
3).
![]() ,
если область
- верхняя половина шара
,
если область
- верхняя половина шара
![]() .
.
Ответ:
![]() .
.
4).
![]() ,
если область
ограничена сферой
,
если область
ограничена сферой
![]() и плоскостями
,
,
.
Ответ:
и плоскостями
,
,
.
Ответ:
![]() .
.
5).
![]() ,
если область
ограничена конусом
,
если область
ограничена конусом
![]() и плоскостью
и плоскостью
![]() .
Ответ:
.
Ответ:
![]() .
.
5-е занятие. Приложения тройного интеграла.
Повторить: формулы объёма и массы тела, координаты центра тяжести.
1. Объём тела вычисляется по формуле:
![]() .
.
2. Если дано некоторое тело
с плотностью
![]() - непрерывной функцией, то масса данного
тела:
- непрерывной функцией, то масса данного
тела:
![]() .
.
3. Координаты центра тяжести однородного
тела:
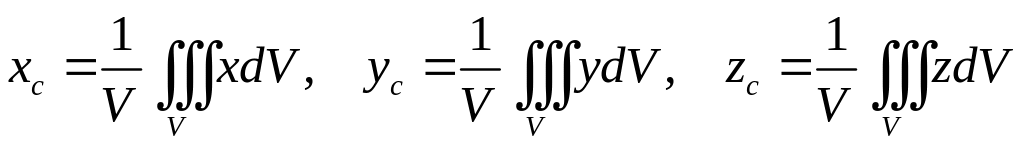 ,
где
- объём данного тела.
,
где
- объём данного тела.
Задания для решения.
1). Вычислить объём тела, ограниченного
поверхностями
![]() .
.
Р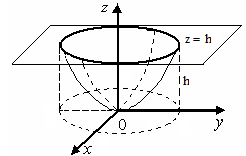 ешение.
Данное тело ограничено снизу параболоидом
ешение.
Данное тело ограничено снизу параболоидом
![]() ,
сверху плоскостью
,
сверху плоскостью
![]() и проецируется в круг
и проецируется в круг
![]() плоскости
.
Переходим к цилиндрическим координатам,
в которых уравнение параболоида
плоскости
.
Переходим к цилиндрическим координатам,
в которых уравнение параболоида
![]() .
Объём тела
.
Объём тела
![]()
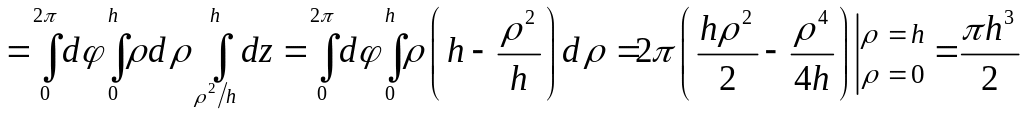 куб. ед.
куб. ед.
2). Вычислить объём тела, ограниченного
поверхностями
![]() ,
,
![]() .
.
Ответ:
![]() куб. ед.
куб. ед.
3). Найти массу куба
![]() ,
если плотность в каждой точке
,
если плотность в каждой точке
![]() .
Ответ:
.
Ответ:
![]() .
.
4). Найти координаты центра тяжести
призмы, ограниченной плоскостями
,
,
,
![]() ,
,
![]() .
.
Решение. Объём тела
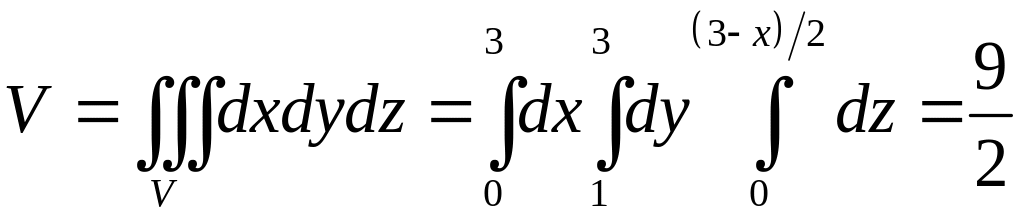 куб. ед. Тогда
куб. ед. Тогда
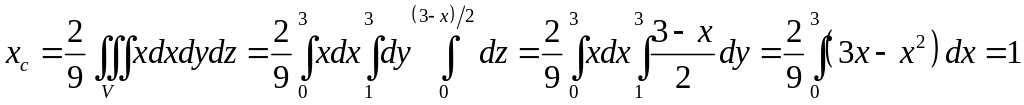 ,
,
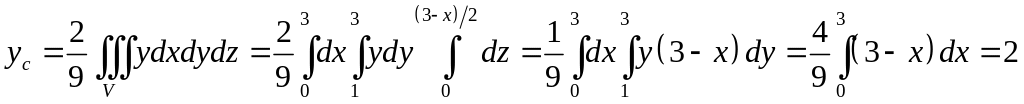 ,
,
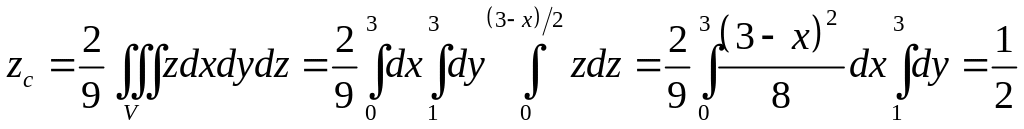 .
Ответ:
.
Ответ:
![]() .
.
5). Найти координаты центра тяжести тела,
ограниченного поверхностями
![]() ,
,
,
,
.
Ответ:
,
,
,
,
.
Ответ:
![]() .
.
6). Найти координаты центра тяжести тела,
ограниченного поверхностями
![]() ,
,
![]() ,
,
![]() ,
.
Ответ:
,
.
Ответ:
![]() .
.
6-е занятие. Контрольная работа по теме «Кратные интегралы».
Повторить: приёмы и способы вычисления двойных и тройных интегралов.
Примерный вариант контрольной работы.
Вычислить интеграл
 ,
где D ограничена
окружностями
,
где D ограничена
окружностями
 ,
,
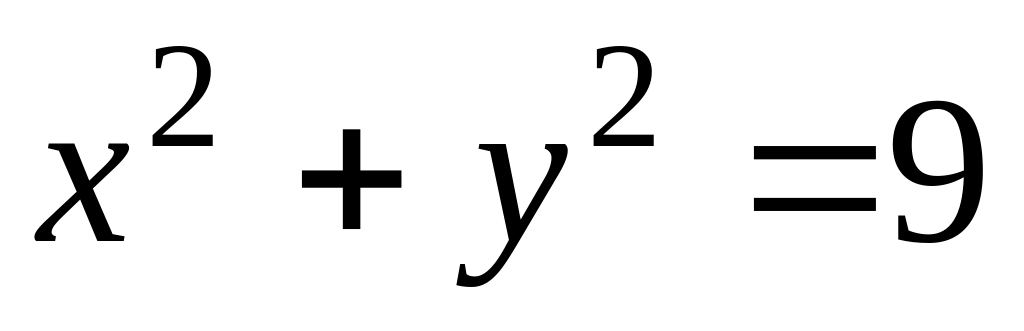 .
.Вычислить интеграл
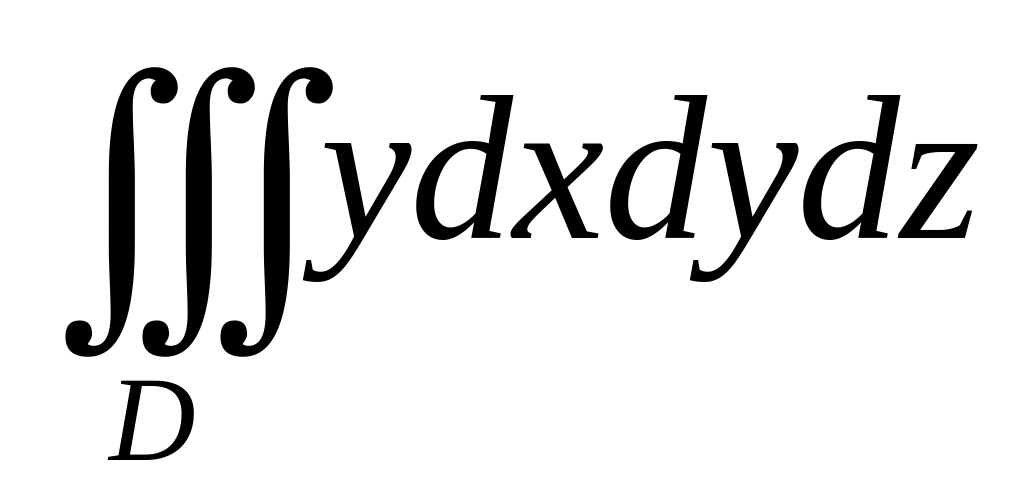 ,
где область D
ограничена плоскостями
,
,
,
,
,
,
где область D
ограничена плоскостями
,
,
,
,
,
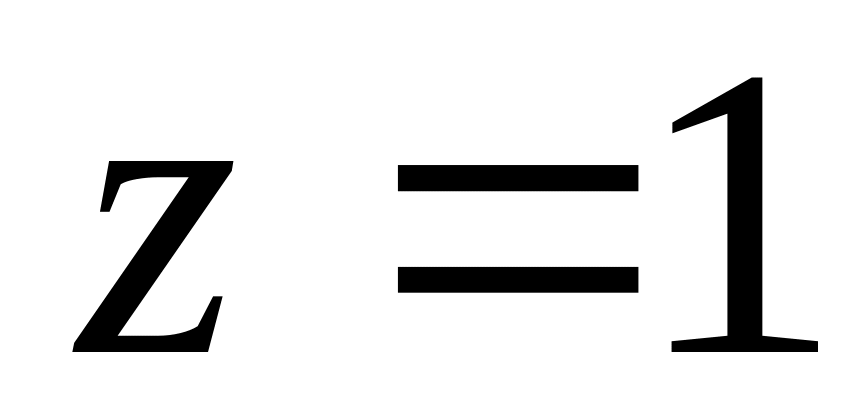 .
.а). Построить на плоскости XOY область интегрирования
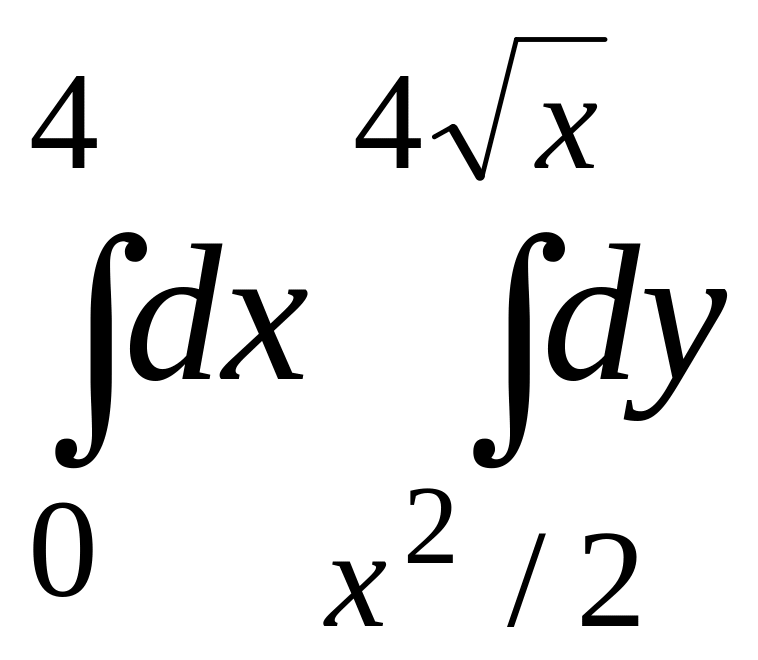 заданного интеграла;
заданного интеграла;
б). Изменить порядок интегрирования и вычислить площадь области при заданном и измененном порядках интегрирования.
7-е занятие. Вычисление криволинейных интегралов.
Повторить: формулы для вычисления криволинейных интегралов I и II рода.
1. Если кривая
![]() задана уравнением
задана уравнением
![]() ,
,
![]() ,
где
,
где
![]() - непрерывно дифференцированная функция,
то
- непрерывно дифференцированная функция,
то
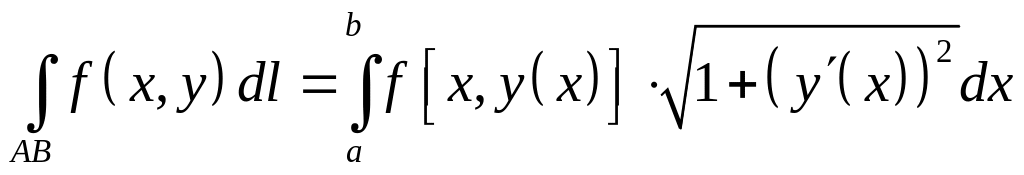 ;
;
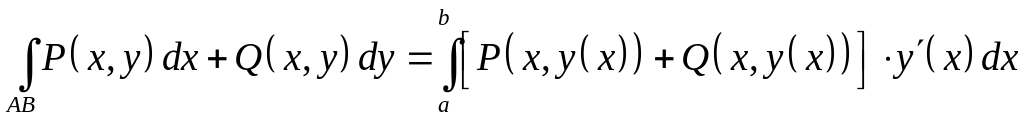 .
.
Если кривая
задана уравнением вида
![]() ,
,
![]() ,
то
,
то
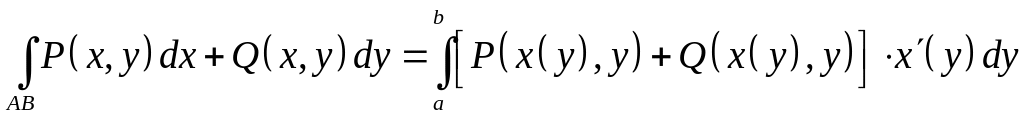 .
.
2. Если кривая задана параметрическими
уравнениями
![]() ,
,
![]() ,
,
![]() ,
где
,
где
![]() и
и
![]() - непрерывно дифференцируемые функции,
причём точке
соответствует значение
- непрерывно дифференцируемые функции,
причём точке
соответствует значение
![]() ,
точке
,
точке
![]() - значение
- значение
![]() ,
тогда
,
тогда
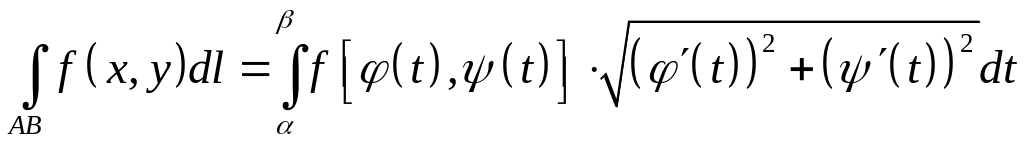 ;
;
 .
.
Задания для решения. Вычислить криволинейные интегралы.
1).
![]() ,
где
,
где
![]() - отрезок прямой от
- отрезок прямой от
![]() до
до
![]() .
.
Решение. Уравнение прямой
![]() ,
отсюда
,
отсюда
![]() ,
значит
,
значит
![]()
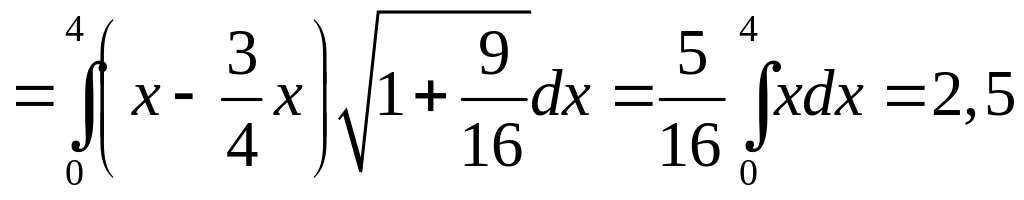 .
.
2).
![]() ,
если
,
если
![]() ,
,
![]() ,
,
![]() .
.
Решение.
![]() ,
,
![]() ,
тогда
,
тогда
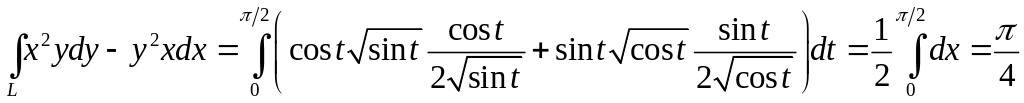 .
.
3).
![]() ,
если путь от
,
если путь от
![]() до
до
![]() - отрезок прямой.
- отрезок прямой.
4).
![]() ,
если
,
если
![]() - ломаная
- ломаная
![]() где
где
![]() ,
,
![]() ,
,
![]() .
.
5).
![]() ,
если
- дуга кривой
,
если
- дуга кривой
![]() от
от
![]() до
до
![]() .
.
6). Найти координаты центра тяжести дуги
циклоиды
![]() ,
,
![]() ,
,
![]() .
.
7). Найти координаты центра тяжести дуги
окружности
![]() в I четверти.
в I четверти.
8). Найти массу дуги окружности
![]() ,
,
![]() ,
если её плотность
,
если её плотность
![]() .
.
Ответы: 3).
![]() .
4).
.
4).
![]() .
5).
.
5).
![]() .
6).
.
6).
![]() .
7).
.
7).
![]() .
8). 2.
.
8). 2.
Приложение. Табличные интегралы.
 ,
, ;
;
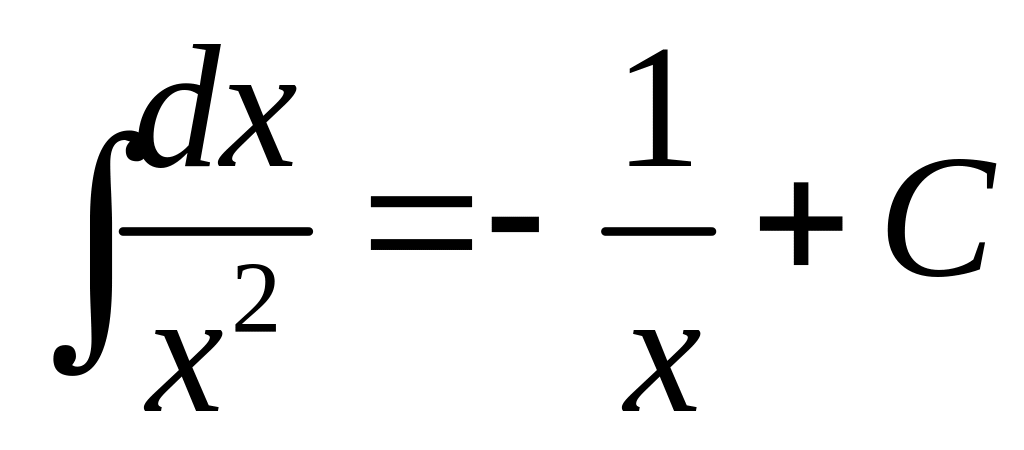 ;
;
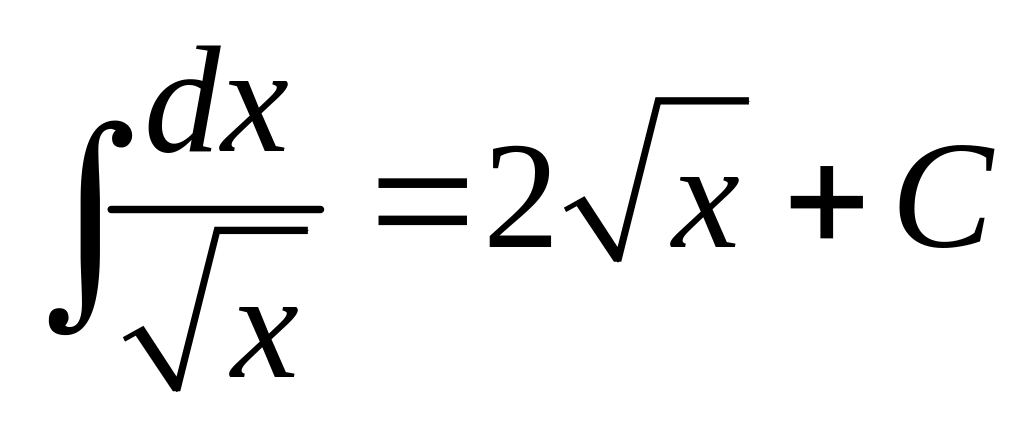 .
. .
.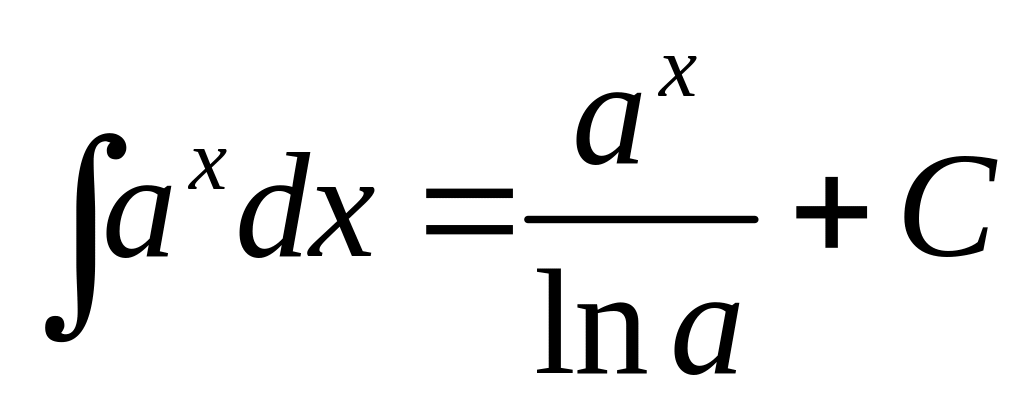 .
.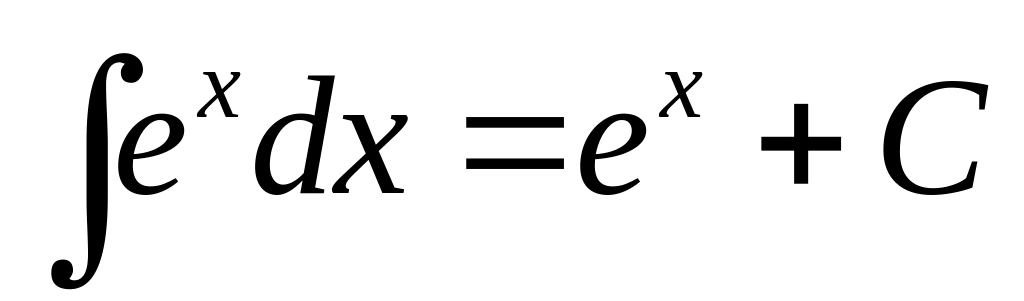 .
.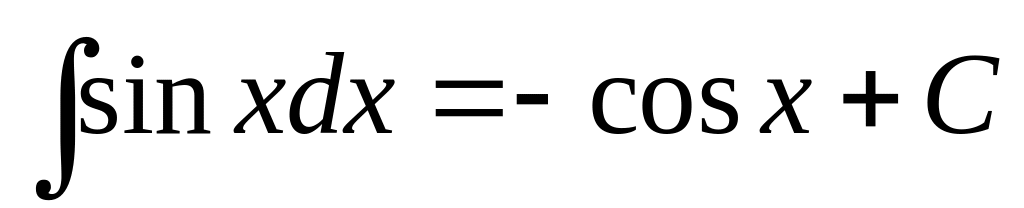 ;
;
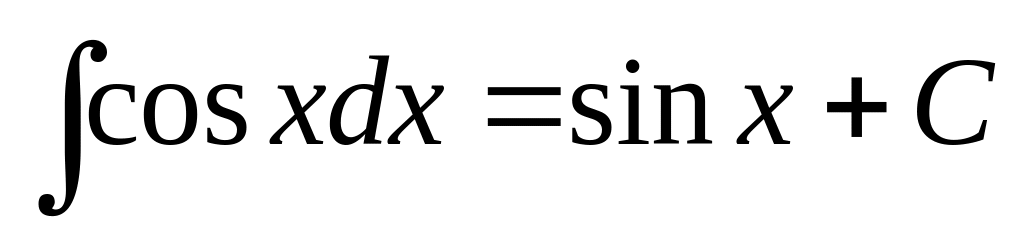 .
.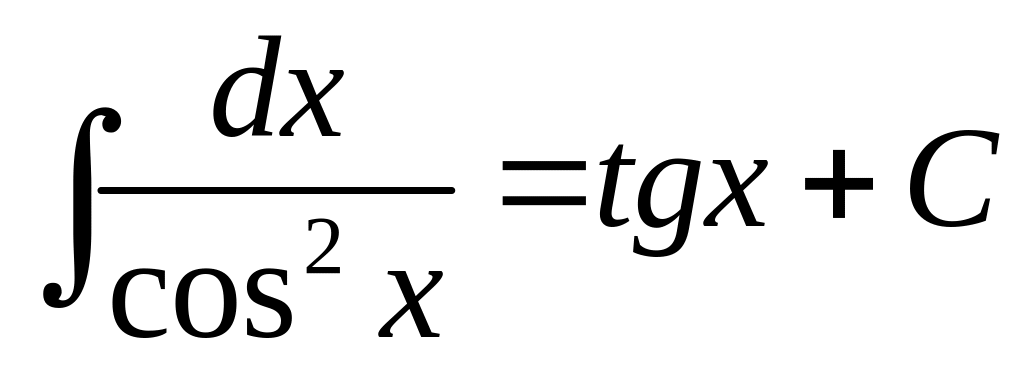 ;
;
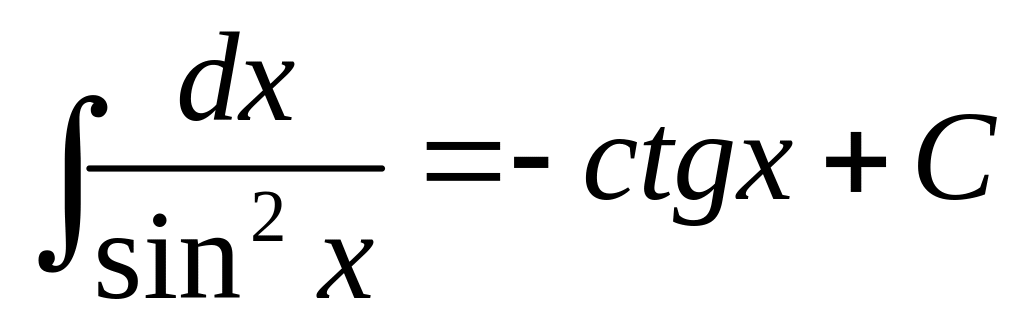 .
.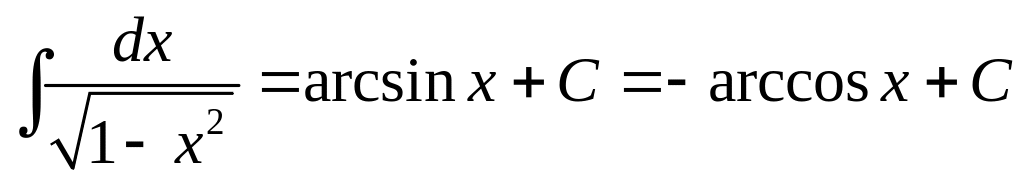 .
.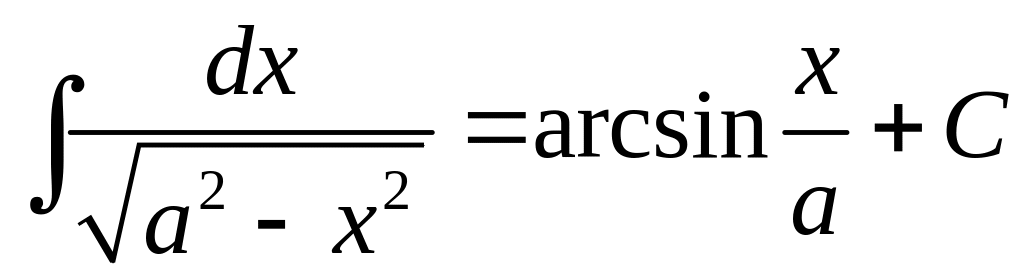 .
.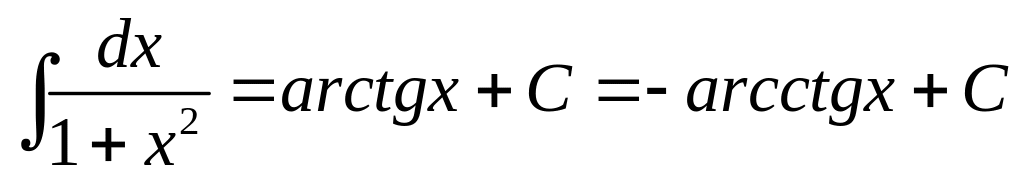 .
.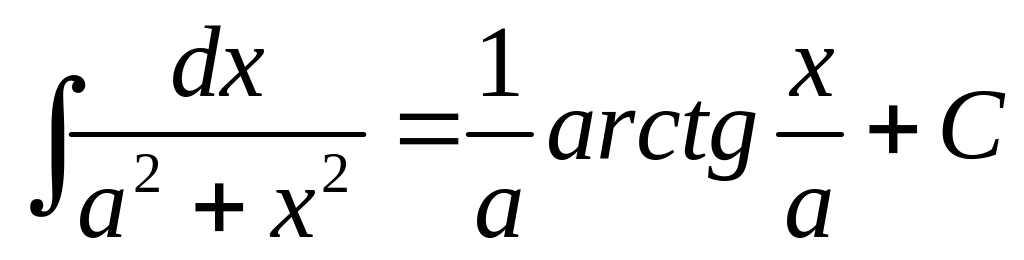 .
.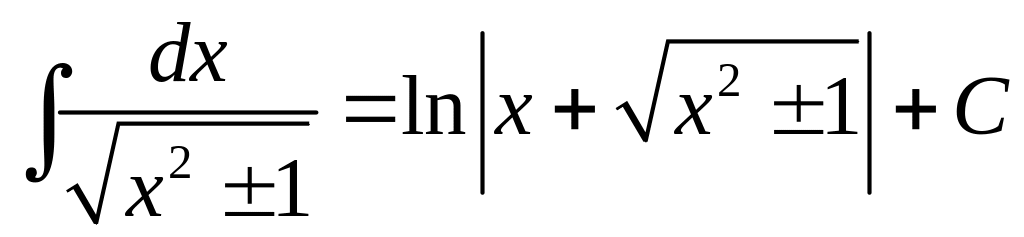 .
.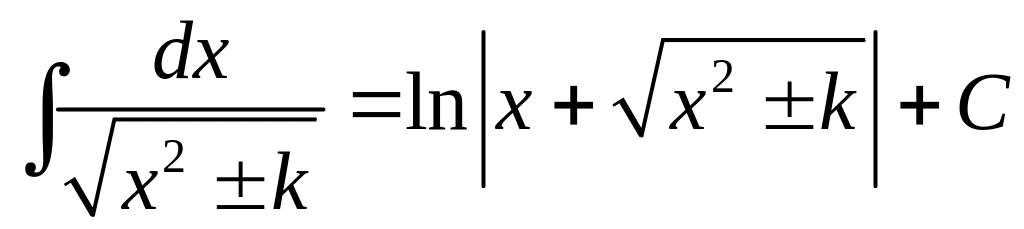 .
.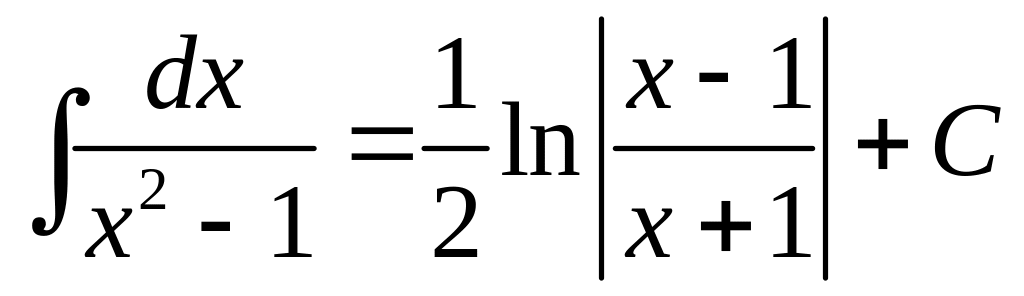 .
.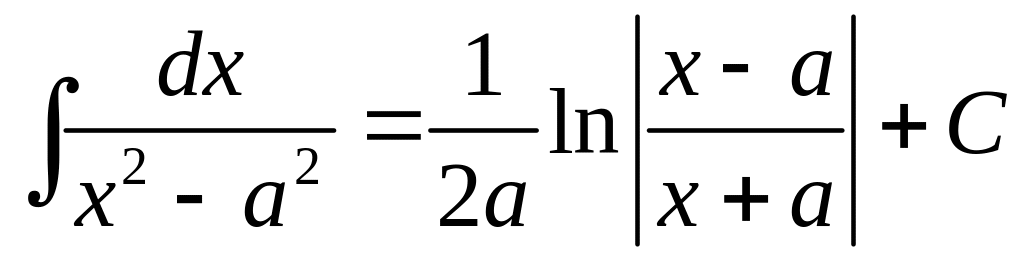 .
.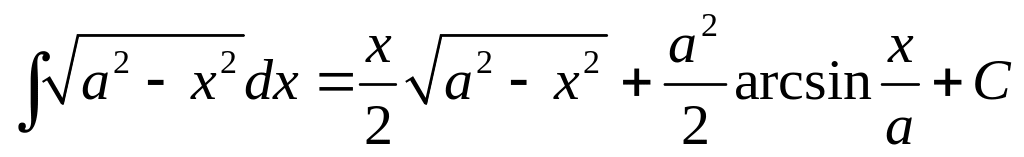 .
. .
.
Библиография
П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова. Высшая математика в упражнениях и задачах. 2 том.
Н. С. Пискунов. Дифференциальное и интегральное исчисления. 2 том.
Д. Письменный. Конспект лекций по высшей математике.
В. С. Шипачёв. Высшая математика.
В.П. Минорский Сборник задач по высшей математике.
В авторской редакции.
Компьютерная вёрстка Шубовича А.А.
Подписано в печать Формат
![]()
Усл. печ. л. 0,7. Тираж 100. Заказ
Издательско-полиграфический комплекс ВГСХА «Нива»
