Упражнения

Записать вид частных решений для данных ЛНДУ, не находя неопределенные коэффициенты:

54. 

    1. ;

    2. ;

    3. ;

    4. ;

    5. ;

    6. ;

    7. ;

    8. ;

54. 

    1. ;

    2. ;

    3. 

55. 1. ;

    2. ;

    3. ;

    4. ;

    5. ;

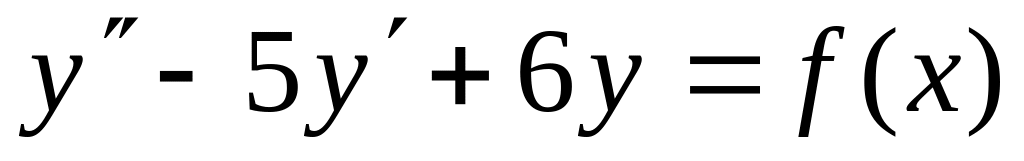
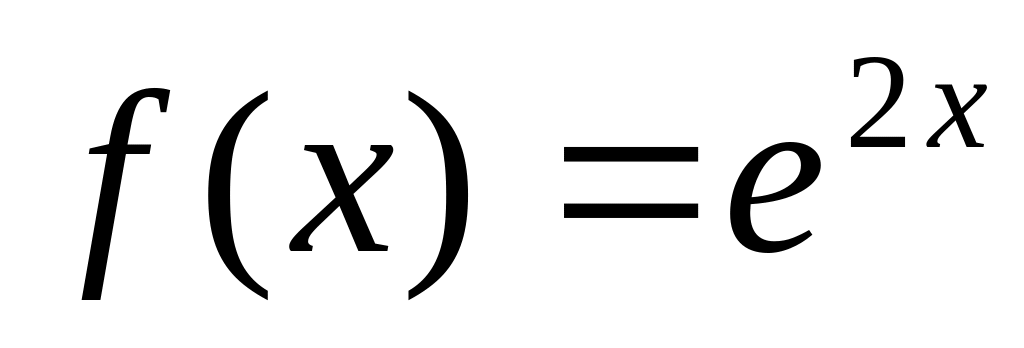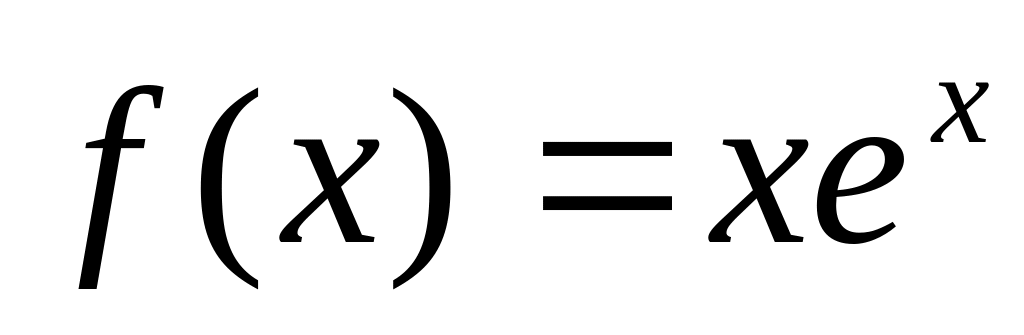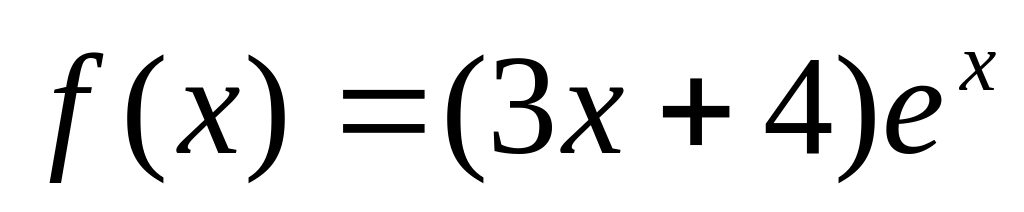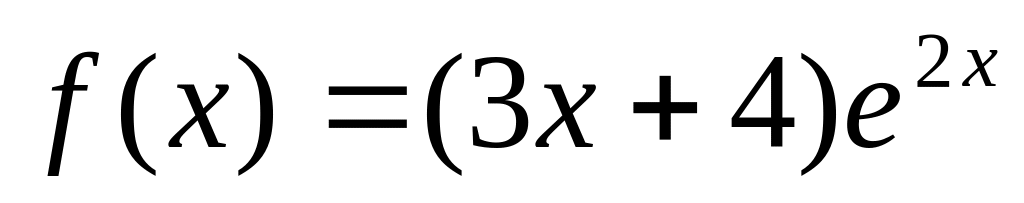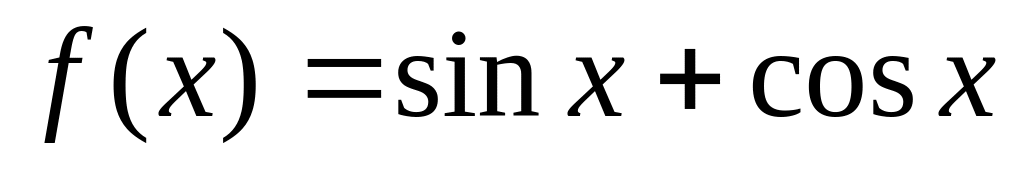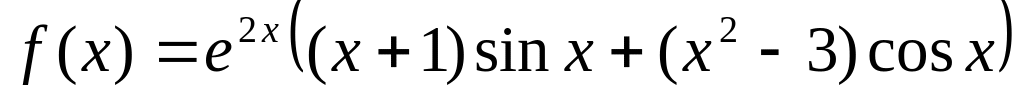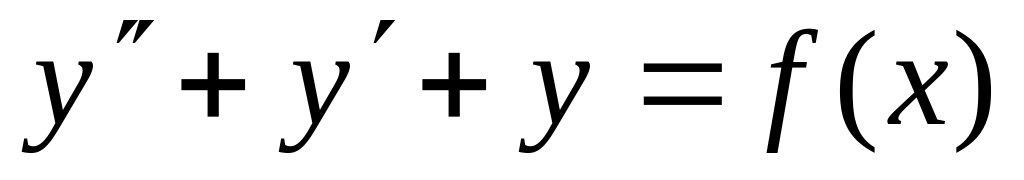
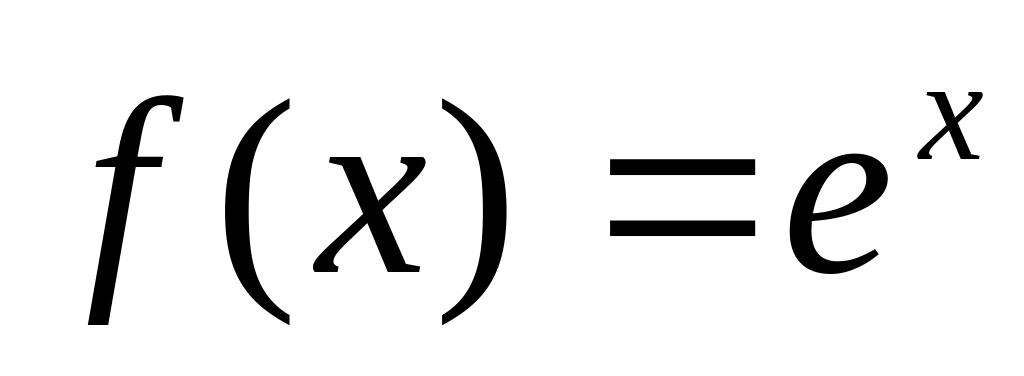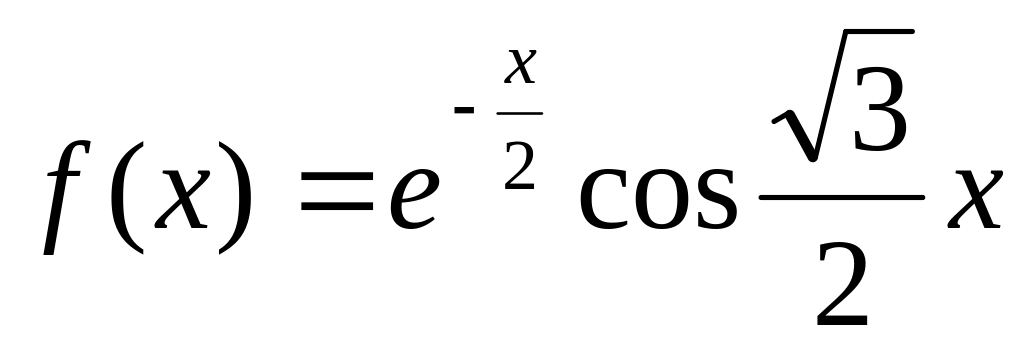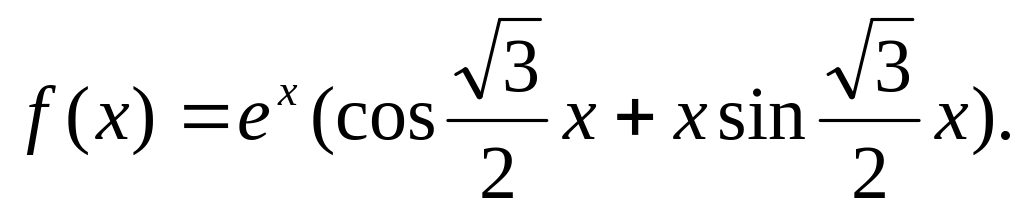
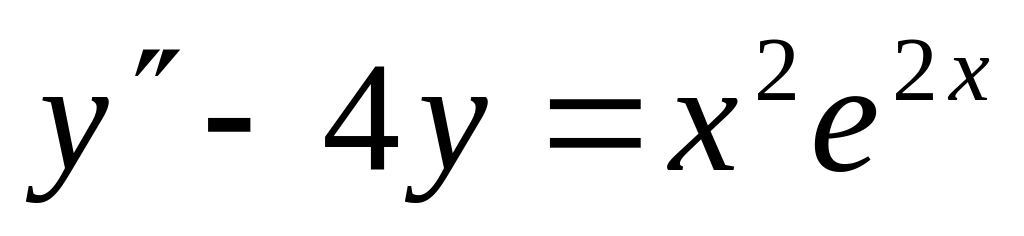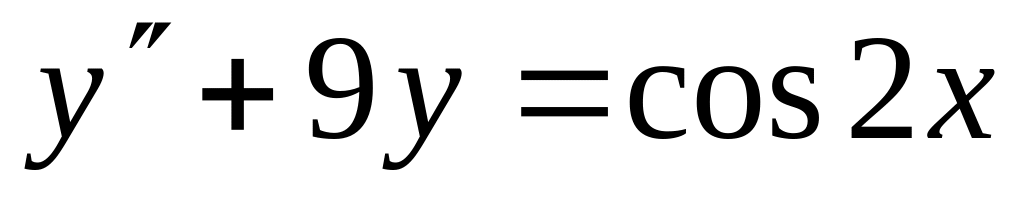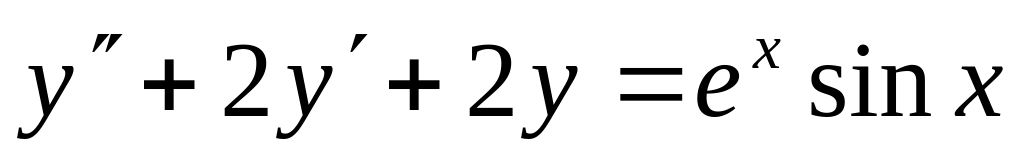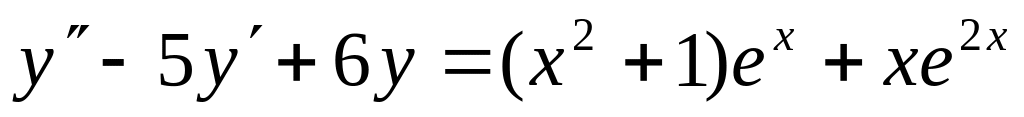54. Найти общие решения ЛНДУ:

    1. ;

    2. ;

    3. ;

    4. ;

    5. ;

    6. ;

    7. .

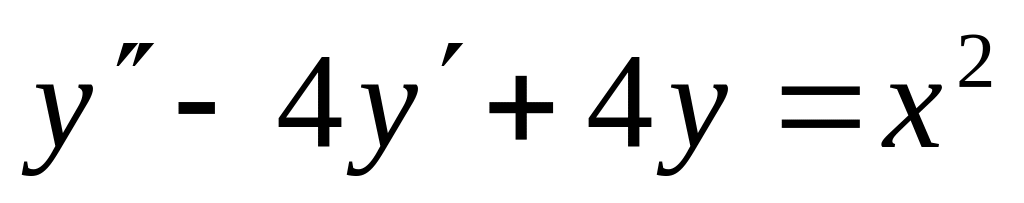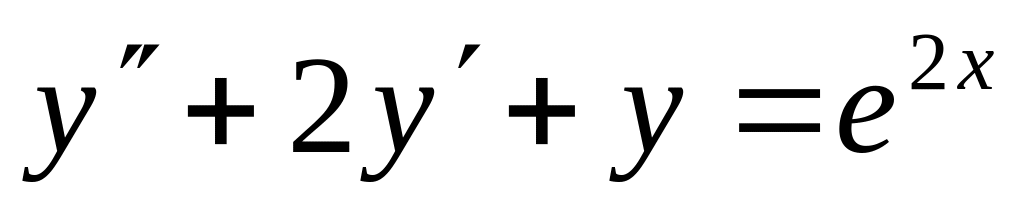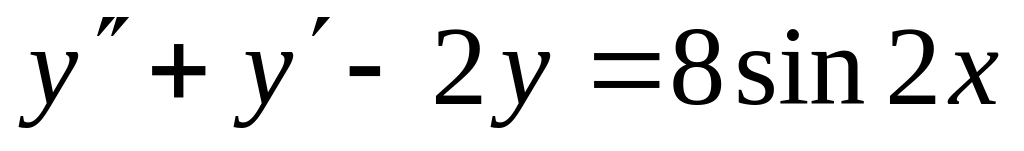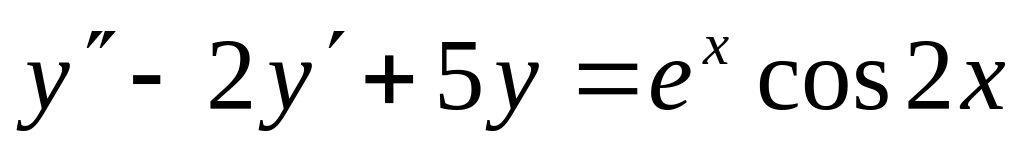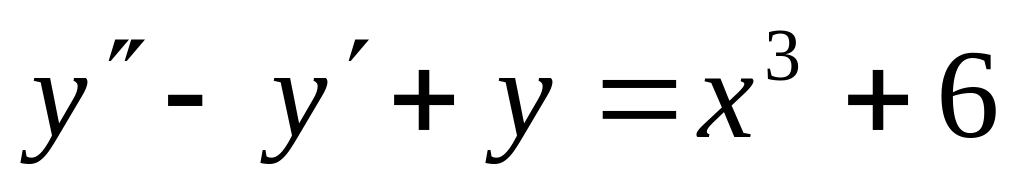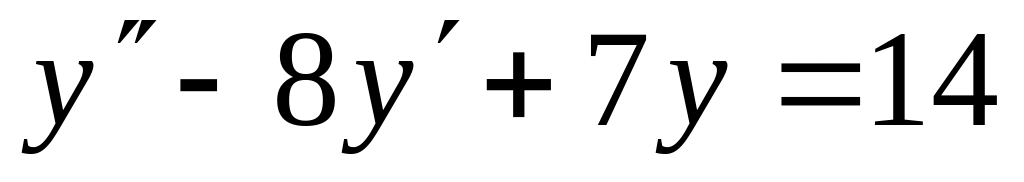54. Найти частные решения ЛНДУ 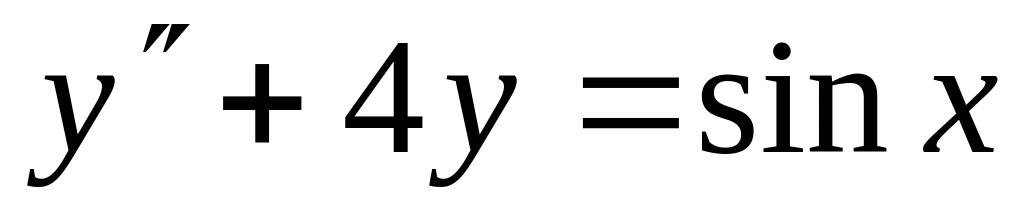, удовлетворяющее начальным условиям y = 1; =1 при х = 0.

*⁾ Функции y1(x) и y2(x) линейно независимы тогда и только тогда, когда их линейная комбинация C1y1(x) + C2y2(x) обращается в нуль лишь при С1 = С2= 0

30