
- •8. Модель парной регрессии
- •9. Оценка параметров модели парной регрессии
- •10. Оценка уравнения парной регрессии
- •11. Множественная регрессия
- •12. Оценка параметров модели парной регрессии
- •13. Оценка уравнения множественной регрессии
- •14. Классификация экономических прогнозов
- •15. Виды временных рядов. Требования, предъявляемые к исходной информации
- •16. Компоненты временных рядов
- •17. Аддитивная и мультипликативная модель
- •18. Метод Фостера-Стюарта «наличия-отсутствия тренда»
- •19. Основные показатели динамики экономических явлений
16. Компоненты временных рядов
Данные, представленные в виде временных рядов, могут содержать два вида компонент — систематическую и случайную составляющие.
Систематическая составляющая является результатом влияния постоянно действующих факторов. Выделяют две основных систематических компоненты временного ряда:
Тренд — это систематическая линейная или нелинейная компонента, плавно изменяющая во времени (Т). Он описывает чистое влияние долговременных факторов.
Циклическая (сезонная) компонента (S).
Сезонность — это периодические колебания уровней временного ряда в течение не очень длительного периода (недели, месяца, максимум — года). Сезонность отражает повторяемость экономических процессов в рамках одного года.
Цикличность - это периодические колебания, выходящие за рамки одного года. Промежуток времени между двумя соседними "вершинами" или "впадианми" в масштабах года считается длиной цикла. Цикличность отражает повторяемость экономических процессов в течение длительных периодов.
Систематические составляющие могут одновременно присутствовать во временном ряду.
Случайной составляющей называется случайный шум, или ошибка, воздействующая на временной ряд нерегулярно (E). Основными причинами случайного шума могут быть факторы резкого и внезапного воздействия , а также воздействие текущих факторов, которое может быть связано, например, с ошибками наблюдений.
17. Аддитивная и мультипликативная модель
В зависимости от характера сезонных колебаний различают два вида моделей – аддитивная и мультипликативная.
По аддитивной модели временной ряд с сезонными колебаниями представляется в виде:

где:
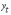 –
значение прогнозируемой переменной
для
–
значение прогнозируемой переменной
для  -го
момента времени;
-го
момента времени;
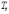 –
трендовая составляющая
;
–
трендовая составляющая
;
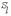 –
сезонная
составляющая
;
–
сезонная
составляющая
;
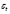 –
случайная ошибка.
–
случайная ошибка.
По мультипликативной модели временной ряд с сезонными колебаниями имеет в вид:
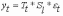
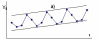
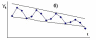
Для решения вопроса о том какая из рассматриваемых моделей должна быть выбрана для конкретного временного ряда, необходимо построить график изменения прогнозируемой величины во времени и проанализировать изменение амплитуды сезонных колебаний (Рис.16.). В случае если амплитуда сезонных колебаний не имеет ярко выраженной тенденции к изменению во времени, то тогда может быть выбрана аддитивная модель (a), в противном случае предпочтительна мультипликативная (б).
18. Метод Фостера-Стюарта «наличия-отсутствия тренда»
Под трендом понимают изменение, определяющее общее направление развития, основную тенденцию временного ряда. Это систематическая составляющая долговременного действия.
Метод Фостера-Стюарта. Этот метод может быть реализован в виде следующей последовательности шагов:
Каждый уровень ряда сравнивается со всеми предшествующими, при этом определяются значения вспомогательных характеристик mt и lt:
-
mt =
{
1 , если yt > yt-1, yt-2 , …, y1
0, в противном случае
Таким образом, mt = 1, если yt больше всех предшествующих уровней, alt = 1, если меньше всех предшествующих уровней.
Вычисляется dt = mt - lt для всех t=2÷n.
n
Находится характеристика D = Σdt
t=2
С помощью критерия Стьюдента проверяется гипотеза о том, что можно считать случайной разностью D-0 (т. е. ряд можно считать случайным, не содержащим тренд).
Для этого определяется
tнабл = D/ σD
где σD – средняя квадратичная ошибка величины D:
Значения σD затабулированы.
Расчетное значение tнабл сравнивается с критическим значением tkp, взятым из таблицы t – распределения Стьюдента для заданного уровня значимости α и числа степеней свободы k = n - 1. Если | tнабл| > tkp, то гипотеза об отсутствии тренда отвергается.
