13. Оценка уравнения множественной регрессии
Практическая значимость уравнения множественной регрессии оценивается с помощью показателя множественной корреляции и его квадрата – показателя детерминации.
Показатель множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком или, иначе, оценивает тесноту совместного влияния факторов на результат.
,
где
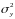– общая дисперсия результативного
признака;
– остаточная дисперсия.
Границы изменения индекса множественной корреляции от 0 до 1. Чем ближе его значение к 1, тем теснее связь результативного признака со всем набором исследуемых факторов.
Индекса
множественной детерминации: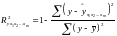 
.
Формула скорректированного индекса множественной детерминации имеет вид:
,
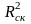
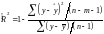(2.17)
где
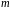– число параметров при переменных
;
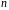– число наблюдений.
Чем
больше величина
,
тем сильнее различия
и
.
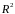Он определяет тесноту связи с
учетом степеней свободы общей и остаточной
дисперсий. Он дает такую оценку тесноты
связи, которая не зависит от числа
факторов и поэтому может сравниваться
по разным моделям с разным числом
факторов.
Нескорректированный
коэффициент множественной детерминации
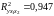оценивает долю вариации результата за
счет представленных в уравнении факторов
в общей вариации результата.
Значимость уравнения множественной регрессии в целом, так же как и в парной регрессии, оценивается с помощью -критерия Фишера:
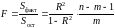, где
– факторная сумма квадратов на одну
степень свободы;
– остаточная сумма квадратов на одну
степень свободы;
– коэффициент (индекс) множественной
детерминации;
– число параметров при переменных
(в линейной регрессии совпадает с числом
включенных в модель факторов);
– число наблюдений. Фактическое значение
частного
-критерия
сравнивается с табличным при уровне
значимости
и числе степеней свободы: 1 и
.
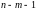Если фактическое значение
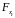превышает
,
то дополнительное включение фактора
в модель статистически оправданно и
коэффициент чистой регрессии
при факторе
статистически значим. Если же фактическое
значение
меньше табличного, то дополнительное
включение в модель фактора
не увеличивает существенно долю
объясненной вариации признака
,
следовательно, нецелесообразно его
включение в модель; коэффициент регрессии
при данном факторе в этом случае
статистически незначим.
14. Классификация экономических прогнозов
В зависимости от объектов прогнозирования принято разделять прогнозы на научно-технические, экономические, социальные, военно-политические и т.д. Однако такая классификация носит условный характер, т.к. между этими прогнозами, как правило, существует множество прямых и обратных связей.
В зависимости от масштабности объекта прогнозирования экономические прогнозы могут охватывать все уровни: от микроуровня (рассматривающего прогнозы развития отдельных предприятий, производств и т.д.) до макроуровня (анализирующего экономическое развитие в масштабе страны) или - до глобального уровня (где существующие закономерности рассматриваются в мировом масштабе).
Но времени упреждения экономические прогнозы делятся на:
• оперативные (с периодом упреждения до одного месяца)
• краткосрочные (период упреждения от одного, нескольких месяцев до года),
•
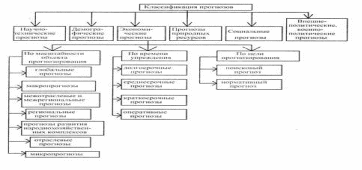среднесрочные
(период упреждения более 1 года, но не
превышает 5 лет),
• долгосрочные (с периодом упреждения более 5 лет).