Постоянное магнитное поле в вакууме. Индукция магн.Поля. Закон био-савара. Магн.Поле прямого и кругового тока.

В пространстве, окружающем токи и постоянные магниты, возникает силовое поле, называемое магнитным.

Магни́тная инду́кция  — векторная величина, являющаяся силовой характеристикой магнитного поля в данной точке пространства. Показывает, с какой силой магнитное поле действует на заряд , движущийся со скоростью .

Более точно,  — это такой вектор, что сила Лоренца , действующая на заряд , движущийся со скоростью , равна

где α — угол между векторами скорости и магнитной индукции.

Также магнитная индукция может быть определена как отношение максимального механического момента сил, действующих на рамку с током, помещенную в однородное поле, к произведению силы тока в рамке на её площадь.

Является основной характеристикой магнитного поля, аналогичной вектору напряжённости электрического поля.

Закон Био́—Савара—Лапла́са — физический закон для определения модуля вектора магнитной индукции в любой точке магнитного поля, порождаемого постоянным электрическим током на некотором рассматриваемом участке. Был установлен экспериментально в 1820 году Био и Саваром. Лаплас проанализировал данное выражение и показал, что с его помощью путём интегрирования, в частности, можно вычислить магнитное поле движущегося точечного заряда, если считать движение одной заряженной частицы током.

Пусть постоянный ток течёт по контуру γ, находящемуся в вакууме,  — точка, в которой ищется поле, тогда индукция магнитного поля в этой точке выражается интегралом (в системе СИ)

Направление перпендикулярно и , то есть перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу нахождения линий магнитной индукции (правилу правого винта): направление вращения головки винта дает направление , если поступательное движение буравчика соответствует направлению тока в элементе. Модуль вектора определяется выражением (в системе СИ)

Магнитное поле прямолинейного тока наблюдают, продев сквозь расположенный горизонтально лист картона вертикальный прямолинейный провод, представляющий собой часть электрической цепи. Опилки-стрелочки при замыкании тока в цепи и после легкого постукивания по листу образуют цепочки в виде окружностей с общим центром на оси тока. Поэтому магнитное поле электрического тока графически изображают в виде линий магнитной индукции, аналогичных линиям напряженности электростатического поля. Линии магнитной индукции представляют собой окружности с центрами на оси тока, расположенные в плоскостях, перпендикулярных направлению тока. Их направление определяют по правилу правого винта: при поступательном движении винта в направлении тока его вращение указывает направление магнитного поля этого тока. Различие между линиями магнитной индукции и линиями напряженности электростатического поля: первые замкнуты и окружают электрический ток; вторые – разомкнуты, начинаются на поверхности положительно заряженных тел и оканчиваются на поверхности отрицательно заряженных.

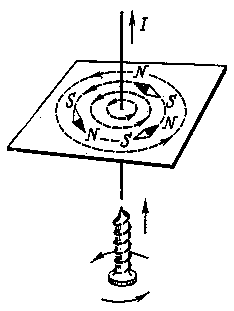
Магнитное поле витка с током, или контура тока, показано рисунке Направление линий магнитной индукции вдоль оси витка укажет магнитная стрелка, помещенная в его центре. Две противоположные стороны обтекаемой током поверхности можно сопоставить с двумя полюсами магнитной стрелки: сторону, из которой линии магнитной индукции выходят – с северным полюсом магнитной стрелки, а в которую они входят – с южным. Направление магнитного поля витка с током можно определить также по правилу правого винта: если поместить острие винта в центре витка и вращать винт в направлении тока, то его поступательное движение укажет направление линий магнитной индукции. Таким образом, существует взаимная связь направлений тока в замкнутом проводнике и его магнитного поля, их «сцепленность»

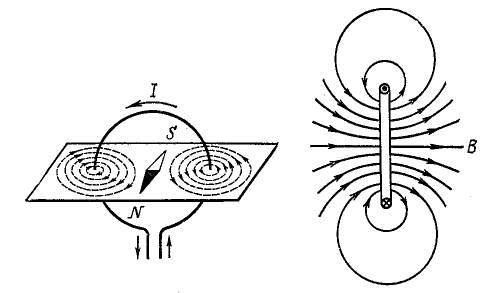
Датский физик X.Эрстед в начале 19 века определил главный в теории электромагнетизма экспериментальный факт, он заключается в следующим, протекание по проводникам электрического тока приводит к появлению в окружающем пространстве магнитного поля.

Этот факт предоставил возможность французскому выдающемуся ученому Лмперу выразить формулировкой закон, который на сегодняшний день имеет название закона полного тока.

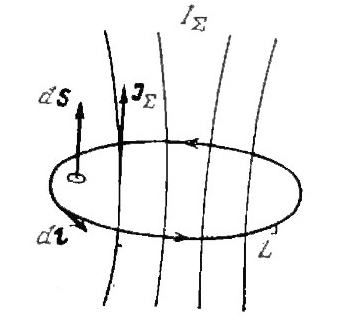
Проанализируем рисунок ниже, воображаемый контур L в пространстве, ограничивающий поверхность S.

На этом контуре установим направление обхода так, чтобы движение с конца вектора вдоль контура элементарной площадки dS прослеживалось в направлении против часовой стрелки.

Далее представим то, что поверхность S пронизывается отдельной системой токов, которая может нести как дискретный характер (к примеру, систему отдельных проводников), так и быть непрерывно распределенной (электронный поток может послужить этому примером). Не обуславливая тем временем физической природы данных токов, будем подразумевать для конкретности, что они распределены непрерывно в пространстве с кое-какой плотностью

То теперь полный ток, пронизывающий контур, найдется в виде

Закон полного тока говорит о том, что циркуляция по контуру L вектора напряженности магнитного поля, инициированного протеканием тока  равна полному току, то есть.

Закон полного тока формулирует соотношение выше в интегральной форме.

В том, чтобы связать плотность полного тока в данной гонке с напряженностью магнитного поля, то есть найти дифференциальную форму данного закона, надлежит употребить знаменитой теоремой Стикса из векторного анализа, которая говорит нам о том, что для каждого векторного поля А верно равенство

Использовав крайнюю формулу и перестроив с её помощью

будем располагать 

откуда получим из-за произвольности выбранного контура

Формула выше несёт в себе закон полного тока в дифференциальной форме. Заметим, что при помощи закона полного тока в интегральной форме удается разрешить ряд задач, связанных по нахождению магнитного поля заданных токов.