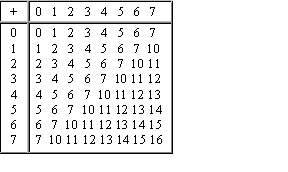- •Лекция 1. Основные понятия и методы теории информатики и кодирования
- •1.1. Информатика как научная дисциплина
- •1.2. Понятие информации и информационных процессов
- •Свойства информации:
- •1.3. Меры и единицы количества и объема информации
- •1.4. Позиционные системы счисления
- •2) Вычитание
- •1.5. Логические основы эвм
- •Логическое сложение (дизъюнкция).
- •Логическое умножение (конъюнкция).
- •Логическое отрицание (инверсия).
- •Логическое следование (импликация).
- •Логическое равенство (эквиваленция).
- •Правила построения таблицы истинности
- •Лекция 2. Технические средства реализации информационных процессов
- •2.1. История развития эвм
- •2.2. Понятие и основные виды архитектуры эвм
- •2.3. Состав и назначение основных устройств персонального компьютера, их характеристики
- •2.4. Запоминающие устройства: классификация, принцип работы, основные характеристики
- •2.5. Устройства ввода/вывода данных, их разновидности и основные характеристики
- •Лекция 3. Программные средства реализации информационных процессов
- •3.1. Понятие и виды программного обеспечения компьютера
- •Программное обеспечение компьютера
- •Базовое (основное)
- •3.2. Операционная система
- •3.3. Файловая система компьютера
- •3.4. Технологии обработки текстовой информации
- •У становка параметров страницы, шрифта и абзаца
- •Многоколончатая верстка
- •Работа со списками
- •Стилевое оформление текста
- •Работа с таблицами в текстовом редакторе
- •Работа с графическими объектами
- •Создание автоматического оглавления
- •3.5. Электронные таблицы
- •Правила записи формул
- •Относительная адресация
- •Абсолютная адресация
- •Сортировка данных
- •Мастер функций
- •Автозаполнение ячеек таблицы данными
- •1 Способ:
- •2 Способ:
- •Математические функции в Excel
- •3) Корень
- •4) Степень
- •7) Сумм
- •8) Суммесли
- •9) Произвед
- •10) Округл
- •13) Целое
- •14) Окрвверх
- •15) Окрвниз
- •16) Округлвверх
- •17) Округлвниз
- •18) Числкомб
- •Нахождение значения функции в некоторой точке
- •Табулирование функции и построение ее графика
- •Построение графиков двух функций на одной диаграмме
- •Решение уравнений методом подбора параметра
- •Статистические функции
- •2) Макса
- •4) Мина
- •5) Медиана
- •6) Мода
- •7) Наибольший
- •8) Наименьший
- •9) Сроткл
- •11) Счётесли
- •10) Считатьпустоты
- •11) Срзнач
- •12) Срзнача
- •Логические функции Microsoft Excel
- •Если(логическое выражение;значение_если_истина;значение_если_ложь)
- •3.6. Технологии хранения, поиска и сортировки информации в базах данных
- •Классификация баз данных
- •Создание таблицы базы данных
- •Заполнение базы данных
- •Поиск данных в базе данных
- •Создание межтабличных связей
- •Работа с запросами
- •Создания запроса на выборку
- •Создания запроса с параметром
- •Создания запроса нас создание таблицы
- •Создания запроса на обновление
- •Создания запроса на удаление
- •Сортировка данных с помощью запроса на выборку
- •Создание отчетов
- •Лекция 4. Модели решения функциональных и вычислительных задач
- •4.1. Моделирование как метод познания
- •4.2. Классификация и формы представления моделей
- •4.3. Методы и технологии моделирования
- •4.4. Формы представления информационных моделей
- •4.5. Формализация
- •4.6. Объекты и их связи
- •4.7. Табличные информационные модели
- •4.8. Иерархические информационные модели
- •4.9. Сетевые информационные модели
- •Лекция 5. Алгоритмизация и программирование
- •5.1. Понятие алгоритма и исполнителя алгоритмов
- •3. С помощью языка программирования.
- •4. С помощью псевдокодов.
- •5.2. Языки программирования и их виды
- •5.3. Среда программирования Turbo Pascal
- •5.4. Язык программирования Pascal
- •ЦПростые типы Строковый тип Структурированные типы Ссылочные типы Процедурные типы Типы данных елые типы
- •Вещественный тип
- •Символьный тип
- •Логический тип
- •5.5. Линейные алгоритмы. Простые операторы языка Pascal
- •Оператор присваивания
- •Операторы вывода
- •1) Оператор Write
- •2) Оператор Writeln
- •Операторы ввода
- •1) Оператор Read
- •2) Оператор Readln
- •5.6. Разветвляющиеся алгоритмы. Условные операторы языка Pascal
- •Условный оператор If
- •5.7. Циклические алгоритмы. Операторы цикла языка Pascal
- •Оператор цикла с предусловием While
- •Оператор цикла с постусловием Repeat .. Until
- •Оператор цикла с параметром (счетчиком) For
- •Лекция 6. Локальные и глобальные сети эвм
- •6.1. Назначение компьютерных сетей
- •6.2. Виды компьютерных сетей
- •6.3. Понятие глобальной компьютерной сети «Интернет»
- •6.4. Основы функционирования Интернета
- •6.5. Адресация в сети Интернет
- •6.6. Службы Интернета
- •5) Программа пересылки файлов ftp.
- •6.7. Способы подключения к Интернету
- •6.7.1. Подключение по коммутируемой телефонной линии с помощью модема
- •6.7.2. Подключение с применением спутниковой антенны
- •6.7.3. Adsl-доступ с применением телефонной линии
- •6.7.4. Подключение к Интернет по выделенной телефонной линии
- •6.7.5. Подключение к Интернет по технологии gprs
- •6.7.6. Подключение к Интернет по технологии Ethernet
- •Список литературы
1.4. Позиционные системы счисления
Система счисления – это способ записи чисел и соответствующие этому способу правила действия над числами.
Существуют позиционные и непозиционные системы счисления.
В непозиционных системах счисления вес цифры (т. е. тот вклад, который она вносит в значение числа) не зависит от ее позиции в записи числа. Так, в римской системе счисления в числе ХХХII (тридцать два) вес цифры Х в любой позиции равен просто десяти.
В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число. Например, в числе 757,7 первая семерка означает 7 сотен, вторая — 7 единиц, а третья — 7 десятых долей единицы.
Сама же запись числа 757,7 означает сокращенную запись выражения
700 + 50 + 7 + 0,7 = 7 . 102 + 5 . 101 + 7 . 100 + 7 . 10-1 = 757,7.
Любая позиционная система счисления характеризуется своим основанием.
Основание позиционной системы счисления — количество различных цифр, используемых для изображения чисел в данной системе счисления.
Для перевода целого десятичного числа N в систему счисления с основанием q необходимо N разделить с остатком ("нацело") на q , записанное в той же десятичной системе. Затем неполное частное, полученное от такого деления, нужно снова разделить с остатком на q , и т.д., пока последнее полученное неполное частное не станет равным нулю. Представлением числа N в новой системе счисления будет последовательность остатков деления, изображенных одной q-ичной цифрой и записанных в порядке, обратном порядку их получения.
Пример: Переведем число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:
![]()

Ответ: 7510 = 1 001 0112 = 1138 = 4B16.
Для перевода правильной десятичной дpоби F в систему счисления с основанием q необходимо F умножить на q , записанное в той же десятичной системе, затем дробную часть полученного произведения снова умножить на q, и т. д., до тех пор, пока дpобная часть очередного пpоизведения не станет pавной нулю, либо не будет достигнута требуемая точность изображения числа F в q-ичной системе. Представлением дробной части числа F в новой системе счисления будет последовательность целых частей полученных произведений, записанных в порядке их получения и изображенных одной q-ичной цифрой. Если требуемая точность перевода числа F составляет k знаков после запятой, то предельная абсолютная погрешность при этом равняется q -(k+1) / 2.
Пример. Переведем число 0,36 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

Для чисел, имеющих как целую, так и дробную части, перевод из десятичной системы счисления в другую осуществляется отдельно для целой и дробной частей по правилам, указанным выше.
Перевод в десятичную систему числа x, записанного в q-ичной cистеме счисления (q = 2, 8 или 16) в виде xq = (anan-1 ... a0 , a-1 a-2 ... a-m)q сводится к вычислению значения многочлена
x10 = an qn + an-1 qn-1 + ... + a0 q0 + a-1 q -1 + a-2 q-2 + ... + a-m q-m средствами десятичной арифметики.
Примеpы:

Кроме десятичной широко используются системы с основанием, являющимся целой степенью числа 2, а именно:
двоичная (используются цифры 0, 1);
восьмеричная (используются цифры 0, 1, ..., 7);
шестнадцатеричная (для первых целых чисел от нуля до девяти используются цифры 0, 1, ..., 9, а для следующих чисел — от десяти до пятнадцати — в качестве цифр используются символы A, B, C, D, E, F).
Полезно запомнить запись в этих системах счисления первых двух десятков целых чисел:
|
|
Рассмотрим основные арифметические операции: сложение, вычитание, умножение и деление. Правила выполнения этих операций в десятичной системе хорошо известны — это сложение, вычитание, умножение столбиком и деление углом. Эти правила применимы и ко всем другим позиционным системам счисления. Только таблицами сложения и умножения надо пользоваться особыми для каждой системы.
1) Сложение
Таблицы сложения легко составить, используя Правило Счета. Сложение в двоичной системе
|
Сложение в восьмеричной системе
|
Сложение в шестнадцатеричной системе
 При
сложении цифры суммируются по разрядам,
и если при этом возникает избыток, то
он переносится влево.
Пример 1.
Сложим числа 15 и 6 в различных системах
счисления.
При
сложении цифры суммируются по разрядам,
и если при этом возникает избыток, то
он переносится влево.
Пример 1.
Сложим числа 15 и 6 в различных системах
счисления.
![]()

Шестнадцатеричная: F16+616
|
Ответ: 15+6 = 2110 = 101012 = 258 = 1516. Проверка. Преобразуем полученные суммы к десятичному виду: 101012 = 24 + 22 + 20 = 16+4+1=21, 258 = 2 . 81 + 5 . 80 = 16 + 5 = 21, 1516 = 1 . 161 + 5 . 160 = 16+5 = 21. |
Пример 2. Сложим числа 141,5 и 59,75.
![]()
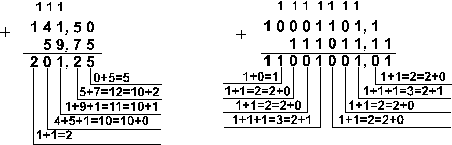
![]()
 Ответ:
141,5 + 59,75 = 201,2510
= 11001001,012
= 311,28
= C9,416
Ответ:
141,5 + 59,75 = 201,2510
= 11001001,012
= 311,28
= C9,416