
Лабораторная работа №81
.docСАНКТ-ПЕТЕРБУРГСКИЙ
ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ОТЧЕТ
по лабораторной работе №8.2
"Исследование эффекта Холла в собственном полупроводнике"
Выполнил: Зуев Иван
Группа: 9132
Факультет: РТ
Санкт-Петербург
2000
ИССЛЕДОВАНИЕ ЭФФЕКТА ХОЛЛА В СОБСТВЕННОМ ПОЛУПРОВОДНИКЕ
Цель работы: изучение действия магнитного поля на движущиеся заряды при исследовании эффекта Холла; определение постоянной Холла, концентрации, подвижностей и средних скоростей упорядоченного движения носителей заряда в собственном полупроводнике.
Приборы и принадлежности: измерительная установка с электромагнитом и датчиком Холла.
![]() (1)
(1)
где
![]() -
коэффициент (постоянная) Холла; В—индукция
магнитного поля; d и
h—ширина и толщина пластины
соответственно. Эффект Холла
объясняется отклонением под действием
силы Лоренца
-
коэффициент (постоянная) Холла; В—индукция
магнитного поля; d и
h—ширина и толщина пластины
соответственно. Эффект Холла
объясняется отклонением под действием
силы Лоренца
![]() носителей заряда Q,
движущихся в магнитном поле со средней
скоростью упорядоченного движения
носителей заряда Q,
движущихся в магнитном поле со средней
скоростью упорядоченного движения
![]()
![]()
В результате на одной
из граней оказывается избыток зарядов,
а на другой (противоположной)
— их недостаток, и возникает
поперечное электрическое поле
![]() .
Квазистационарное распределение зарядов
в поперечном направлении будет достигнуто,
когда действие на заряды электрической
силы
.
Квазистационарное распределение зарядов
в поперечном направлении будет достигнуто,
когда действие на заряды электрической
силы
![]() уравновесит действие силы Лоренца, при
этом
уравновесит действие силы Лоренца, при
этом
![]() .
.
В электронных (или
дырочных) полупроводниках или металлах
![]() ,
где е—элементарный заряд;
,
где е—элементарный заряд;
![]() —концентрация
основных носителей заряда (
—концентрация
основных носителей заряда (![]() для полупроводников р-типа и
для полупроводников р-типа и
![]() =n
для полупроводников n-типа; n
и p - концентрации
электронов и дырок соответственно),
тогда
=n
для полупроводников n-типа; n
и p - концентрации
электронов и дырок соответственно),
тогда
![]()
В результате, с учетом
выражения (1), получаем
![]() .
В собственных полупроводниках концентрации
электронов и дырок равны: n=p=
.
В собственных полупроводниках концентрации
электронов и дырок равны: n=p=![]() ,
здесь
,
здесь
![]() - собственная концентрация носителей
заряда; ток складывается из электронной
и дырочной составляющих:
- собственная концентрация носителей
заряда; ток складывается из электронной
и дырочной составляющих:
![]()
где
![]() - средние скорости упорядоченного
движения и подвижности (
- средние скорости упорядоченного
движения и подвижности (![]() )
электронов и дырок соответственно;
-удельная электропроводность
полупроводника, равная
)
электронов и дырок соответственно;
-удельная электропроводность
полупроводника, равная
![]() (2)
(2)
здесь
![]() - отношение подвижностей электронов и
дырок. Тогда постоянная Холла для
собственного полупроводника
- отношение подвижностей электронов и
дырок. Тогда постоянная Холла для
собственного полупроводника
![]() (3)
(3)
Таким образом, определив
постоянную Холла, можно найти концентрацию
носителей заряда, а по знаку постоянной
Холла — судить о
принадлежности полупроводника к n-типу
или к p-типу. Обычно в металлах и
полупроводниках n-типа
![]() ,
а в полупроводниках p-типа
,
а в полупроводниках p-типа
![]() .
В собственном полупроводнике знак
холловской разности потенциалов
определяется знаком заряда носителей,
имеющих большую подвижность. Обычно
.
В собственном полупроводнике знак
холловской разности потенциалов
определяется знаком заряда носителей,
имеющих большую подвижность. Обычно
![]() ,
и в собственном полупроводнике
,
и в собственном полупроводнике
![]() .
.
Измерив, кроме постоянной
Холла
![]() ,
удельную электропроводность ,
можно найти (при известном значении b)
подвижности
,
удельную электропроводность ,
можно найти (при известном значении b)
подвижности
![]() и
и
![]() носителей заряда. Выражения для
носителей заряда. Выражения для
![]() и
и
![]() получаются из соотношений
(2) и (3).
получаются из соотношений
(2) и (3).
САНКТ-ПЕТЕРБУРГСКИЙ
ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
по лабораторной работе №8.2
"Исследование эффекта Холла в собственном полупроводнике"
Протокол наблюдений
|
N |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Iэм+(А) |
|
|
|
|
|
|
|
|
|
Ux(mV) |
|
|
|
|
|
|
|
|
|
Iэм-(А) |
|
|
|
|
|
|
|
|
|
Ux(mV) |
|
|
|
|
|
|
|
|
Выполнил: Зуев Иван Проверил:
Факультет: РТ
Группа: 9132
Санкт-Петербург
2000
|
B |
0,15 |
0,3 |
0,45 |
0,6 |
0,75 |
0,9 |
1,05 |
1,2 |
|
B |
-0,15 |
-0,3 |
-0,45 |
-0,6 |
-0,75 |
-0,9 |
-1,05 |
-1,2 |
![]() ,
где k
– коэффициент пропорциональности.
Рассчитаем а, как тангенс угла наклона
касательной, на каждом промежутке:
,
где k
– коэффициент пропорциональности.
Рассчитаем а, как тангенс угла наклона
касательной, на каждом промежутке:
![]() .
Подсчитаем и найдем по этой формуле для
все а:
.
Подсчитаем и найдем по этой формуле для
все а:
|
а |
|
-4,8 |
-6,4 |
-4,8 |
-4,8 |
-6,4 |
-6,4 |
-3,2 |
|
а |
|
-4,8 |
-6,4 |
-6,4 |
-4,8 |
-6,4 |
-4,8 |
-4,8 |
Н айдем
среднее а:
айдем
среднее а:
![]() .
Найдем его СКО:
.
Найдем его СКО:
![]() ,
подсчитаем погрешность косвенных
измерений:
,
подсчитаем погрешность косвенных
измерений:
![]() ,
В итоге получаем, что
,
В итоге получаем, что
![]() 0.5.
Аналогично подсчитаем и для с, тогда
получим, что с=0,150,8.
Построим по этим данным график:
0.5.
Аналогично подсчитаем и для с, тогда
получим, что с=0,150,8.
Построим по этим данным график:
С
помощью графика и уравнения следует,
что
![]() ;
;
![]() и, т.к. a=-5,37,
мы можем подсчитать Rx:
и, т.к. a=-5,37,
мы можем подсчитать Rx:
![]()
![]() .
Подсчитаем его погрешность и запишем
результат:
.
Подсчитаем его погрешность и запишем
результат:
![]() .
.
Теперь
зная Rx
мы
можем вычислить ni
выражая
из формулы:
![]() Таким
образом находим ni,
подставляя туда значения мы получаем:
Таким
образом находим ni,
подставляя туда значения мы получаем:
![]() .
После этого найдем удельную
электропроводность полупроводника:
.
После этого найдем удельную
электропроводность полупроводника:
![]() ,
подставим наши значения и тогда получаем:
,
подставим наши значения и тогда получаем:
![]() .
Теперь мы можем найти подвижность дырок
и электронов:
.
Теперь мы можем найти подвижность дырок
и электронов:

![]() 9,79,
следовательно
-=979.
9,79,
следовательно
-=979.
Следуя
дальше мы видим, что
![]() С
другой стороны:
С
другой стороны:
![]() ,
тогда
,
тогда
![]() Значит E
будет
равно:
Значит E
будет
равно:
![]() .
Теперь мы можем найти средние скорости
дырок и электронов:
.
Теперь мы можем найти средние скорости
дырок и электронов:
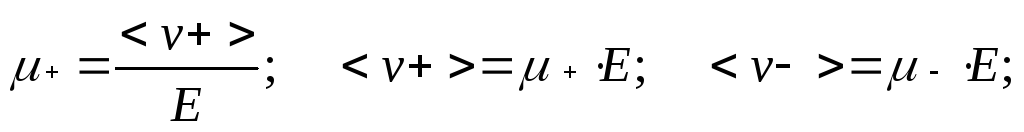
![]() и
<->=6531
м/с. Сравним их со средней скоростью
теплового движения:
и
<->=6531
м/с. Сравним их со средней скоростью
теплового движения:
![]()
Вывод: В результате выполнения данной работы мы смогли изучить эффект Холла, определить значения подвижностей и скоростей движения дырок и электронов, а также постоянную Холла Rx, которая в результате вычислений получилась отрицательной, что говорит о том, что данный полупроводник является полупроводником n-типа. Значения средних скоростей упорядоченного движения дырок и электронов оказались значительно ниже, чем средняя скорость теплового движения электронов.
