1.2.12.2 Кручение стержня с круглым поперечным сечением

Под кручением понимается такой вид нагружения, при котором в поперечных сечениях стержня возникает только крутящий момент.д.ругие силовые факторы равны нулю. При расчете стержня на кручение решают две основные задачи. Требуется определить напряжения и найти угловые перемещения в зависимости от внешних моментов. Механизм деформирования стержня с круглым сечением представляют следующим образом: считают, что каждое поперечное сечение под действием внешних моментов поворачивается в своей плоскости как жесткое целое. Это - гипотеза плоских сечений. Выделим из стержня двумя поперечными сечениями элемент dz, а из него двумя цилиндрическими поверхностями с радиусами  и  + d выделим элементарное кольцо.

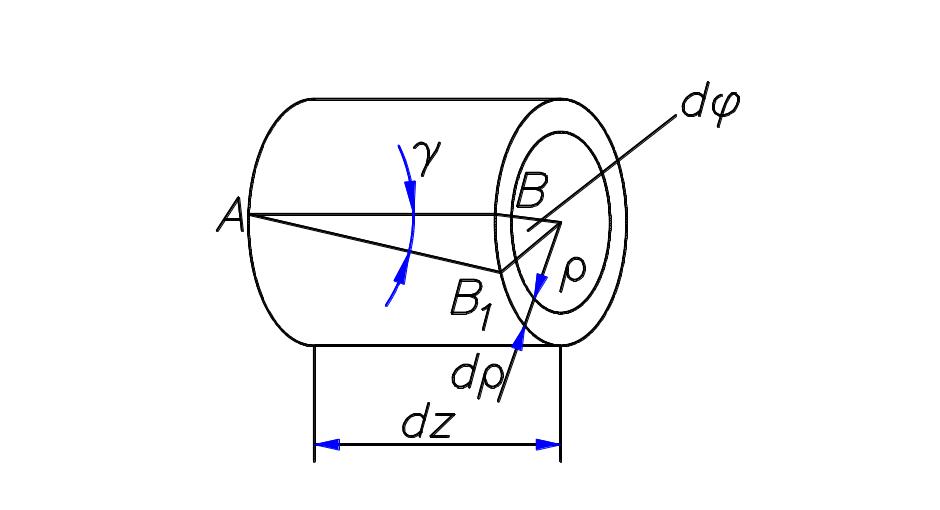
Правое торцевое сечение при кручении поворачивается относительно левого на угол d. Образующая цилиндра АВ поворачивается при этом на угол  и занимает положение АВ. Отрезок ВВ равен с одной стороны , а с другой (поскольку углы малые). Угол  представляет собой не что иное, как угол сдвига цилиндрической поверхности. Обычно обозначают .

Эта величина называется относительным углом закручивания. С учетом этого получаем .

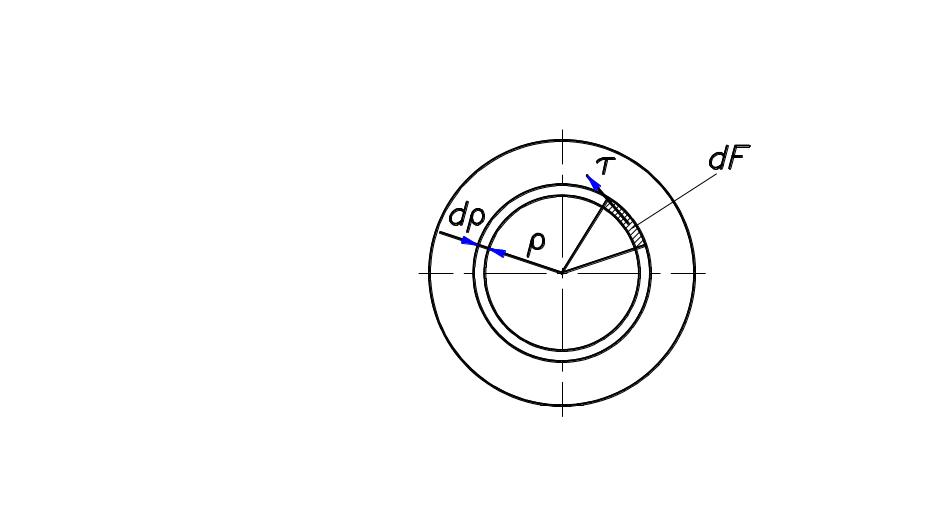
По закону Гука для сдвига . Крутящий момент, вызывающий в кольце такие напряжения .

Подставив сюда значение , получим . Интеграл (см⁴) называется полярным моментом инерции сечения J_р.

Таким образом, или . Произведение называют жесткостью стержня при кручении.

На основе всего изложенного решение названных выше основных задач при расчете на кручение выглядит следующим образом, если М_к по длине не меняется:

,

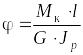где l - расстояние между сечениями, для которых определяется .

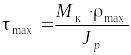
Величина 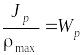называется полярным моментом сопротивления (см³). Окончательно .

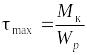Величины геометрических характеристик сечения J_p и W_p можно найти интегрированием. Для круглого сплошного сечения получим

, .

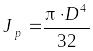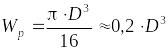Для кольцевого сечения

, .

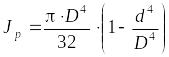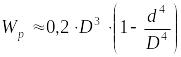Аналогичные решения существуют для некруглых сечений, но они более сложны.

1.2.13. Геометрические характеристики плоских поперечных сечений стержня

Для решения задач, прежде всего, связанных с изгибом, возникает необходимость оперировать некоторыми геометрическими характеристиками поперечных сечений стержня.

1.2.13.1 Статические моменты

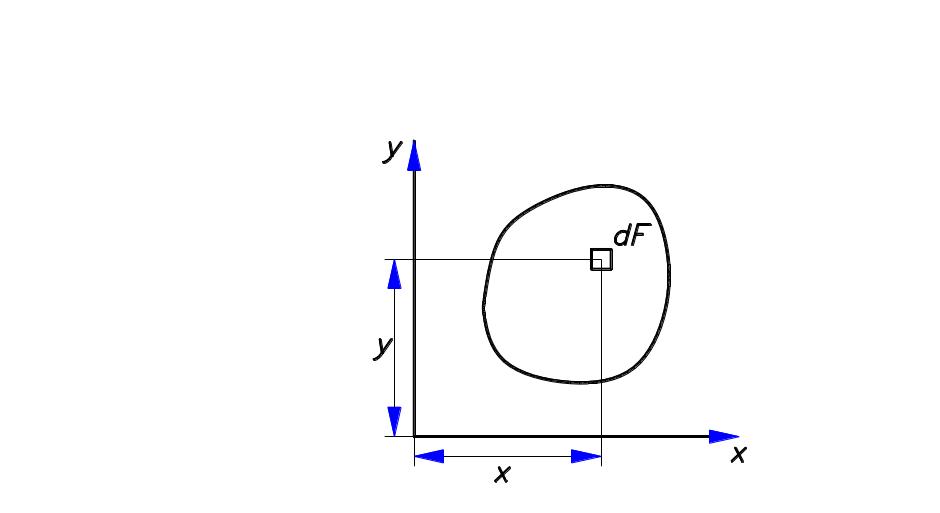
Для некоторого поперечного сечения возьмем интегралы по всей площади сечения

, .

Первый интеграл называется статическим моментом сечения относительно оси х, второй - относительно оси у. При параллельном переносе осей статический момент меняется на величину, равную произведению площади F на расстояние между осями.

Очевидно, можно подобрать такое положение оси, при котором статический момент относительно этой оси обращается в нуль. Такая ось называется центральной. Точка пересечения центральных осей называется центром тяжести сечения.

1.2.13.2 Моменты инерции сечения

Рассмотрим еще три следующих интеграла

; ; .

Первые два интеграла называется осевыми моментами инерции сечения относительно осей х и у. Третий - центробежный момент инерции относительно осей х, у. Минимальный момент инерции получается относительно центральной оси.

Следует отметить еще одно определение: оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты принимают экстремальные значения, называются главными осями. Осевые моменты инерции относительно главных осей называются главными моментами инерции.