Ких-фильтры. Методы синтеза.

Класс последовательностей конечной длины (КИХ-последовательности) обладает некоторыми свойствами, желательными с точки зрения построения фильтров. Например, никогда не возникает вопрос об устойчивости и физической реализуемости фильтров, поскольку КИХ-последовательности гарантируют устойчивость. Более того, КИХ-последовательности можно выбрать так, чтобы фильтры имели строго линейные фазовые характеристики. Поэтому, используя КИХ-последовательности, можно проектировать фильтры с произвольной амплитудной характеристикой.

Существуют три основных метода синтеза КИХ-фильтров:

• метод взвешивания (метод «окна»);

• метод частотной выборки;

• метод оптимальных фильтров.

Свойства КИХ-фильтров

Имеется много причин, побуждающих к изучению способов проектирования КИХ-фильтров. Основными достоинствами этих фильтров являются:

1. Легко создавать КИХ-фильтры со строго линейной фазовой характеристикой (постоянной групповой задержкой). Во многих случаях, когда проектируется фильтр с произвольной амплитудной характеристикой, это упрощает задачу аппроксимации.

2. КИХ-фильтры, реализуемые нерекурсивно, т.е. с помощью свертки, всегда устойчивы.

3. При нерекурсивной реализации КИХ-фильтров шумы округления, возникающие за счет выполнения арифметических операций с конечной точностью, легко минимизировать.

4. КИХ-фильтры можно эффективно реализовывать при помощи методов быстрой свертки, основанных на применении алгоритма БПФ.

Недостатки КИХ-фильтров следующие:

1. Для аппроксимации фильтров, частотные характеристики которых имеют острые срезы, требуется импульсная характеристика с большим числом отсчетов N. Следовательно, возрастает объем вычислительных операций.

2. Задержка в КИХ-фильтрах с линейной фазовой характеристикой не всегда равна целому числу интервалов дискретизации.

Характеристики КИХ-фильтров с линейной фазовой характеристикой

Пусть {h(n)} – физически реализуемая последовательность конечной длины, заданная на интервале. Ееz-преобразование равно

. (3.1)

Преобразование Фурье от {h(n)}

(3.2)

является периодическим по частоте с периодом , т.е.

. (3.3)

Рассматривая только действительные последовательности {h(n)}, получим дополнительные ограничения на функцию, представив ее через амплитуду и фазу:

. (3.4)

Потребуем при расчете КИХ-фильтров строго линейной фазовой характеристики, и рассмотрим, при каких условиях импульсная характеристика фильтра h(n)будет это обеспечивать. Требование линейности фазовой характеристикиимеет вид

, (3.5)

где - постоянная фазовая задержка, выраженная через число интервалов дискретизации. Используя (3.4) и (3.5) соотношение (3.2) переписывается в виде:

. (3.6)

Приравнивая действительные и мнимые части, и деля друг на друга правые и левые части полученных равенств, можно получить уравнение, решением которого будут следующие значения:

, (3.7)

. (3.8)

Смысл их заключается в следующем. Условие (3.7) означает, что для каждого Nсуществует только одна фазовая задержка, при которой может достигаться строгая линейность фазовой характеристики фильтра. Из условия (3.8) следует, что при заданном, удовлетворяющем условию (3.7), импульсная характеристика должна обладать симметрией.

Рассмотрим использование условий (3.7) и (3.8) для случаев четного и нечетногоN. ЕслиN- нечетно, то задержка в фильтре равна целому числу интервалов дискретизации. Типичная импульсная характеристика фильтра с линейной фазой для случаяN=11 приведена на рис. 3.1. Типичная импульсная характеристика фильтра с линейной фазой при четномNпоказана на рис. 3.2. ЗдесьN=10.

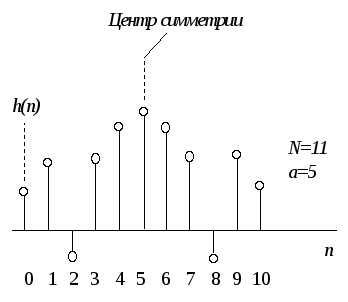
Рис.3.1. N – нечетно.

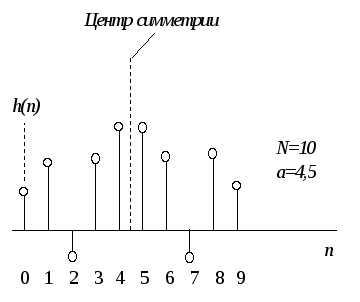
Рис.3.2. N – четно.

Расчет КИХ-фильтров методом взвешивания

Как было сказано ранее, частотную характеристику любого цифрового фильтра можно представить рядом Фурье:

, (3.9)

где

. (3.10)

Видно, что коэффициенты Фурье совпадают с коэффициентами импульсной характеристики цифрового фильтра. Использование этих соотношений для проектирования КИХ-фильтра связано с двумя трудностями. Во-первых, импульсная характеристика фильтра имеет бесконечную длину, поскольку суммирование в (3.9) производится в бесконечных пределах. Во-вторых, фильтр физически нереализуем, так как импульсная характеристика начинается в , т.е. никакая конечная задержка не сделает фильтр физически реализуемым.

Один из возможных методов получения КИХ-фильтра, аппроксимирующего заданную функцию , заключается в усечении бесконечного ряда Фурье (3.9) за. Однако простое усечение ряда приводит к явлению Гиббса, которое проявляется в виде выбросов и пульсаций до и после точек разрыва в аппроксимируемой частотной характеристики. Причем, максимальная амплитуда пульсаций частотной характеристики не уменьшается с увеличением длины импульсной характеристики, т.е. учет все большего числа членов ряда Фурье не приводит к уменьшению максимальной амплитуды пульсаций. Вместо этого уменьшается ширина выброса. Поэтому простое усечение ряда Фурье (3.9) не приводит к приемлемой аппроксимации идеального фильтра нижних частот (к чему необходимо стремиться). Этот метод непригоден для проектирования КИХ-фильтров.

Лучшие результаты дает метод, основанный на использовании весовой последовательности конечной длины w(n), называемой окном, для модификации коэффициентов Фурье в формуле (3.9) с тем, чтобы управлять сходимостью ряда Фурье. Для большинства приемлемых окон преобразование Фурье последовательностиw(n)имеет главный лепесток, содержащий почти всю энергию окна, и боковые лепестки, которые обычно быстро затухают. Чтобы получить КИХ-аппроксимацию функции, формируется последовательность, равная нулю за пределами интервала. Поскольку результирующая характеристика фильтра равна свертке идеальной частотной характеристики и частотной характеристика окна, то ширина переходных полос зависит от ширины главного лепестка функции. Кроме того, на всех частотахвозникают ошибки аппроксимации, имеющие вид пульсаций частотной характеристики, которые обусловлены боковыми лепестками функции.

Из приведенного выше следует, что оптимальное окно должно иметь во-первых, минимальную ширину главного лепестка частотной характеристики, во-вторых, минимальную площадь под боковыми лепестками. К сожалению, эти два требования несовместимы и необходим компромиссный вариант.

Далее рассмотрим некоторые виды окон.

Прямоугольное окно

N-точечное прямоугольное окно, соответствующее простому усечению ряда Фурье, описывается весовой функцией

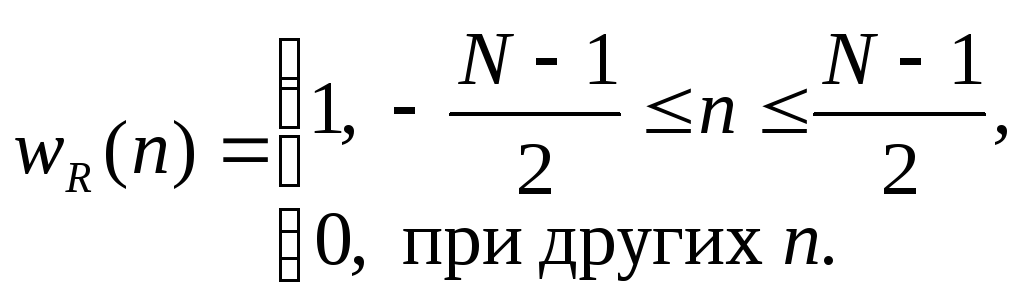(3.11)

Частотная характеристика прямоугольного окна описывается соотношением

. (3.12)

Ее график представлен на рис. 3.3.

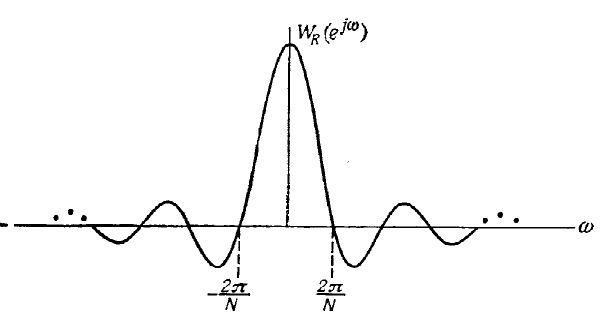
Рис. 3.3. Частотная характеристика прямоугольного окна (N=25).

«Обобщенное» окно Хэмминга

Обобщенное окно Хэмминга имеет вид

(3.13)

причем . Случайсоответствует окну Ханна (hanning), случай- окну Хэмминга. Частотную характеристику этого окна можно выразить через частотную характеристику прямоугольного окна (рис. 3.4):

. (3.14)

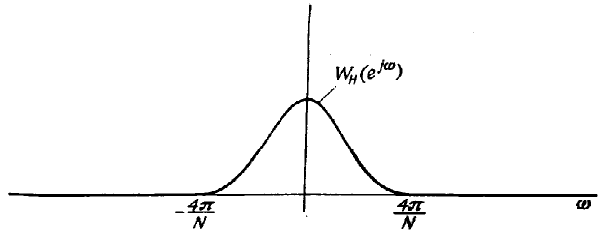
Рис.3.4. Частотная характеристика окна Хэмминга .

Окно Кайзера

Задача расчета хороших окон фактически сводится к математической задаче отыскания ограниченных во времени функций, преобразования Фурье которых наилучшим образом аппроксимируют функции, ограниченные по частоте, т.е. имеют минимальную энергию за пределами заданного интервала частот. Одним из решений такой задачи является окно Кайзера:

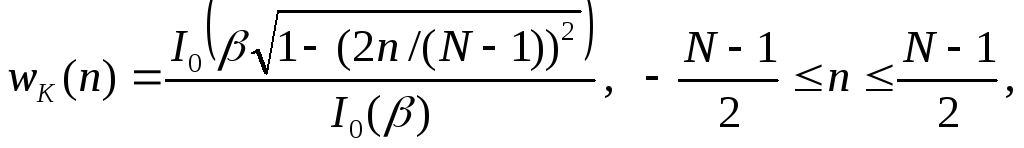(3.15)

где - константа, определяющая компромисс между максимальным уровнем боковых лепестков и шириной главного лепестка частотной характеристики окна, а- функция Бесселя нулевого порядка. Окно Кайзера является по существу оптимальным окном в том смысле, что оно представляет последовательность конечной длины, которая имеет минимум энергии спектра за пределами некоторой заданной частоты.

Прочие окна

Существует еще много различных окон. Вот некоторые из них.

Окно Блэкмана:

. (3.16)

Окно Фейера (треугольное окно):

(3.17)

Окно Ланцоша:

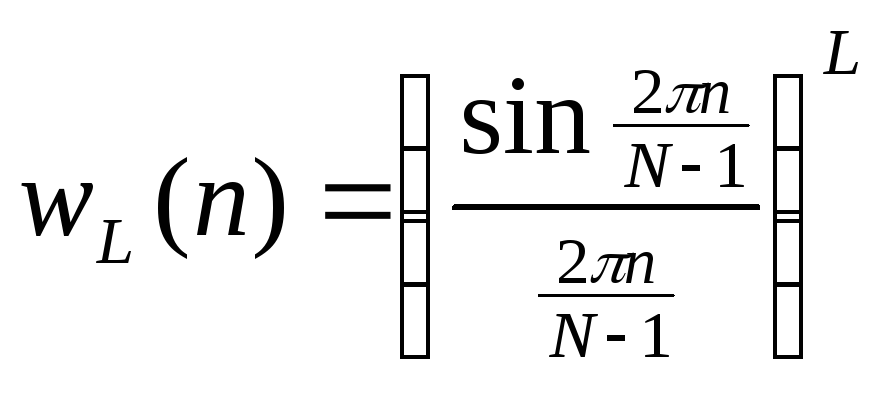, (3.18)

где L– положительное целое число.

Последние два окна основываются на методах суммирования рядов Фурье для ускорения их сходимости. Так же существуют окна, полученные согласно некоторым критериям оптимальности (окна Долфи-Чебышева, окно Каппелини, и т.д.).

Особенности использования метода взвешивания

Метод взвешивания весьма удобен для проектирования КИХ-фильтров, однако он обладает некоторыми особенностями, которые могут препятствовать применению окон. Прежде всего необходимо иметь выражения для коэффициентов ряда Фурье:

. (3.19)

Когда характеристика имеет сложный вид или не может быть просто преобразована в математическое выражение, формула (3.19) может оказаться громоздкой и неудобной для интегрирования.

Еще одна особенность метода взвешивания заключается в отсутствии достаточной гибкости при проектировании фильтров. Например, при расчете ФНЧ обычно трудно определить граничную частоту полосы пропускания, поскольку окно «размывает» разрыв идеальной характеристики.

Вышеупомянутые ограничения метода взвешивания не препятствуют его широкому применению.

Чтобы определить невзвешенные коэффициенты Фурье в том случае, когда аналитическое выражение для h(n)громоздко или неудобно для интегрирования, интеграл можно аппроксимировать суммой по следующей формуле

. (3.20)

Ясно, что значения (3.20) можно эффективно вычислять с помощью M-точечного ОДПФ последовательности. Поскольку формула (3.20) является дискретным аналогом формулы (3.19), легко показать, что ростомMразличие междуh(n)иуменьшается.

Расчет КИХ-фильтров методом частотной выборки

КИХ-фильтр может быть однозначно задан коэффициентами импульсной характеристики {h(n)}, так и коэффициентами ДПФ частотной характеристики{H(k)}.Обе последовательности связаны соотношениями:

ДПФ, (3.21)

ОДПФ. (3.22)

Из формулы (3.22) сразу вытекает прямой способ получения импульсной характеристики фильтра. Такой фильтр имеет частотную характеристику, значения которой равны H(k)вNравноотстоящих на оси частот точках.

К сожалению, эта прямая процедура не представляет практического интереса, так как невозможно предсказать поведение частотной характеристики между частотными выборками.

Для того, чтобы получить фильтры с линейной фазой, частотные выборки должны быть симметричными по амплитуде и иметь линейную антисимметричную фазу в интервале . Учитывая то, что будет использоваться ОДПФ, удобнее выразить условия симметрии на интервале. Ели частотные выборки записаны в виде, то условия симметрии при нечетномNможно записать в виде

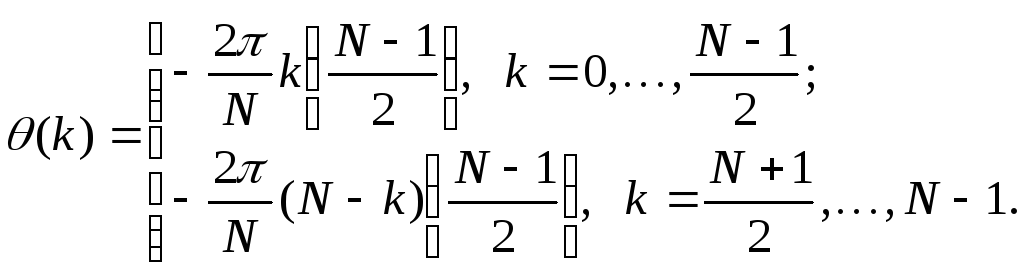(3.23)

Для улучшения качества аппроксимации часть частотных отсчетов имеет смысл сделать независимыми переменными. Значения этих независимых переменных обычно рассчитывают методами оптимизации, таким образом, чтобы минимизировать некоторую простую функцию ошибки аппроксимации.

Можно сформулировать основную идею метода частотной выборки. Искомую частотную характеристику можно аппроксимировать ее отсчетами, взятыми в N равноотстоящих точках, а затем путем интерполяции получить результирующую частотную характеристику, которая будет проходить через исходные отсчеты. Ошибка интерполяции для фильтров с достаточно гладкими частотными характеристиками обычно имеет небольшую величину. В случае селективных фильтров частотные отсчеты в переходных полосах остаются незаданными переменными, значения которых подбираются с помощью алгоритма оптимизации. Для выполнения необходимой минимизации можно использовать простые методы линейного программирования.

Проектирование оптимальных фильтров

Смысл слова оптимальный заключается в следующем: оптимальными являются те фильтры, для которых максимальная ошибка в полосе пропускания и (или) в полосе задерживания минимальна по сравнению с любыми другими фильтрами, которые можно получить, изменяя значения n выборок в переходной полосе.

Рассмотрим подход к расчету КИХ-фильтров при котором минимизируется максимальная ошибка аппроксимации.

Пусть - заданная (желаемая) частотная характеристика,- аппроксимирующая функция,- положительная весовая функция, позволяющая определять ошибки для различных интервалов. Тогда взвешенная ошибка аппроксимациипо определению равна

. (3.24)

Задачу чебышевской аппроксимации можно сформулировать как задачу поиска (а точнее коэффициентов, через которые можно выразить), которая минимизирует максимум модуля ошибкив тех частотных полосах, где выполняется аппроксимация:

, (3.25)

где A – совокупность всех интересующих частотных полос.