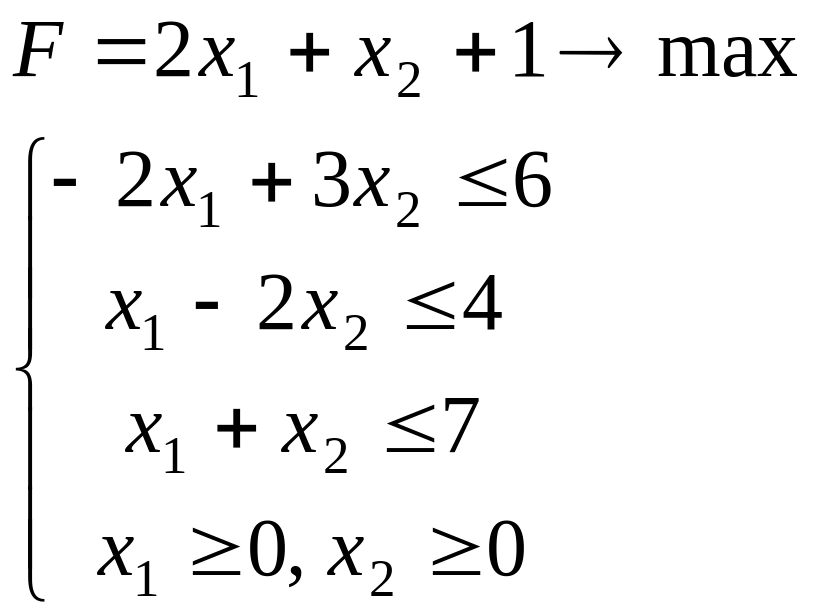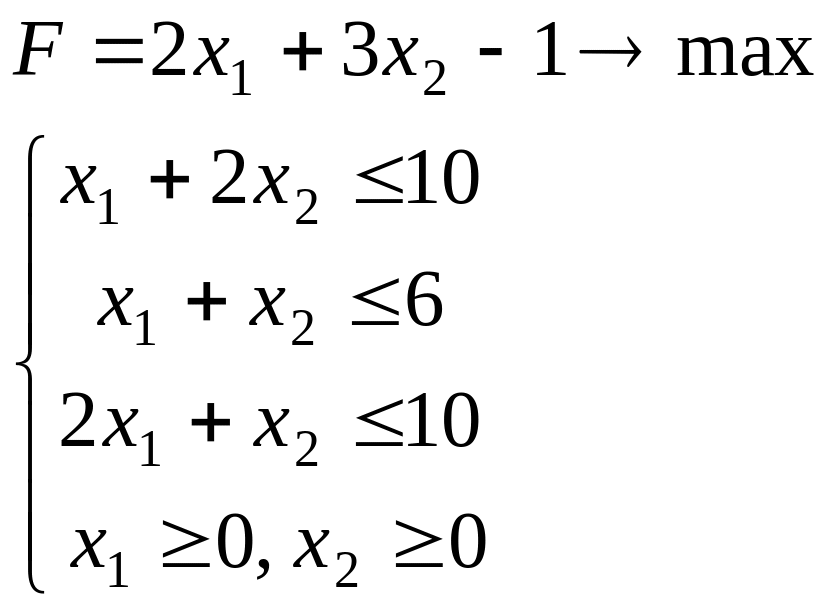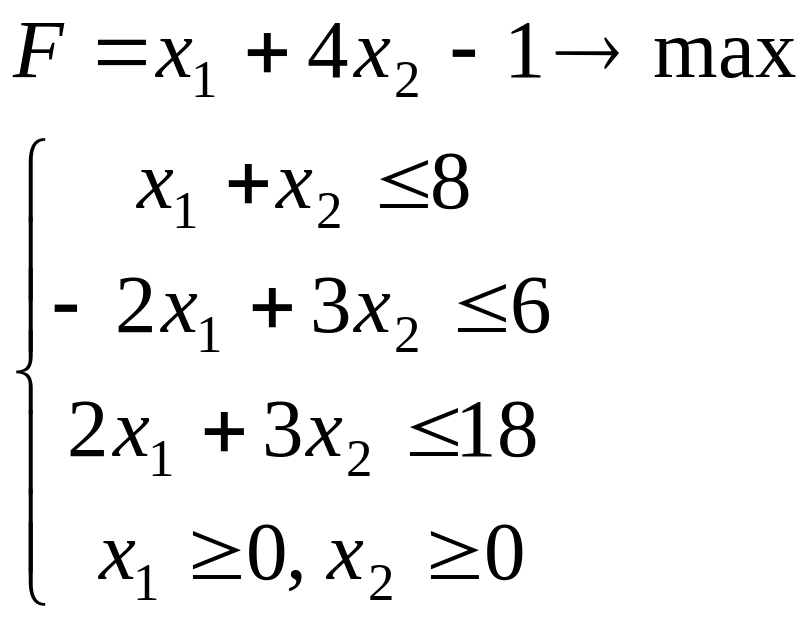РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТОРГО-ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ

КРАСНОДАРСКИЙ ФИЛИАЛ

КАФЕДРА МАТЕМАТИКИ И ПРИКЛАДНОЙ ИНФОРМАТИКИ

Контрольная работа Дисциплина: "Математика"

для студентов 2 курса заочного отделения

специальностей:

080109 «Бухгалтерский учет анализ и аудит»,

080102 «Мировая экономика», 080105 «Финансы и кредит»

080401 «Товароведение и экспертиза товаров» (по областям применения)

080502 «Экономика и управление на предприятии»

080507 «Менеджмент организации»

к.ф.-м.н., доцент

Камалян С.Р.

Краснодар - 2010

Учебный план предусматривает выполнение двух контрольных работ. Контрольная работа № 1 состоит из 2 заданий, контрольная работа № 2 – из 3 заданий. Для каждого задания имеется 10 вариантов. Номера вариантов заданий, подлежащих выполнению студентами, определяются по спискам студентов, приведённым ниже.

В контрольных работах задания записывать в обычном порядке: 1, 2, 3. Условие задачи можно не переписывать, но обязательно указывать номер варианта. К каждой задаче записывать ответ.

Например:

Задача 1.

Вариант 2.

… Решение задачи…

Ответ: …

Контрольная работа № 2

Задание 1. Решить графически задачу ЛП.

Вариант, №	Задача ЛП	Вариант, №	Задача ЛП
1.		6.
2.		7.
3.		8.
4.		9.
5.		10.

Задание 2. Решить стандартную задачу ЛП симплекс-методом и указать, какие из ресурсов являются дефицитными и избыточными.

Вариант,№	c1		c2			c3		a11		a12		a13		a21		a22		a23		a31		a32		a33			b1		b2		b3
1.		8		7	6		2		3		4		1		4		5		-4		-5		-3			15		18		-10
2.		6		5	9		3		4		5		4		6		5		-4		-7		-8			40		15		-20
3.		3		5	6		2		4		5		-3		-2		-5		5		6		6			50		-20		40
4.		9		6	4		5		7		4		-5		-4		-2		2		1		3			24		-10		6
5.		3		4	1		-5		-3		-4		3		2		2		4		1		5			-40		55		20
6.		4		5	8		-9		-8		-6		3		2		4		5		3		2			-40		30		20
7.		5		7	6		4		2		1		3		2		3		-2		-3		-5			30		60		-40
8.		7		1	3		2		3		4		-3		-4		-6		4		1		9			60		-40		90
9.		4		2	3		-5		-1		-2		2		4		1		4		5		3			-10		6		30
10.		7		3	8		2		5		6		2		3		6		-3		-2		-6		15			30		-9

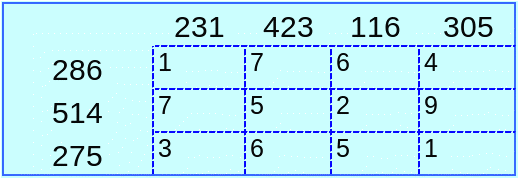
Задание 1. Решить ТЗ, заданную своей таблицей, методом потенциалов. (Слева – мощности поставщиков, сверху – мощности потребителей, в ячейках – тарифы.)

Вариант, №	Таблица ТЗ

Задание 2. Предприятие (игрок A) планирует выпуск продукции на квартал, рассматривая несколько различных вариантов своей деятельности (стратегии A ₁, A ₂, …). Конкурирующее предприятие (игрок B) может выбрать различные варианты поведения на рынке (стратегии B ₁, B ₂, …). Прогнозируемая прибыль предприятия A за квартал в зависимости от сложившейся ситуации задаётся платёжной матрицей, определяющей соответствующую матричную игру (МИ). Требуется: 1) упростить платёжную матрицу путём отбрасывания доминируемых стратегий игроков A и B; 2) вычислить нижнюю и верхнюю цену игры, найти гарантирующие стратегии игроков A и B и установить, имеется ли в заданной МИ седловая точка; 3) найти оптимальную смешанную стратегию игрока A и цену игры графическим методом; 4) для определения оптимальной смешанной стратегии игрока B составить стандартную задачу ЛП, решить её симплекс-методом, найти оптимальную смешанную стратегию и вычислить цену игры; 5) рассмотреть статистическую игру, заданную исходной неупрощённой платёжной матрицей, и определить оптимальные стратегии игрока A в соответствии с критерием Вальда, критерием Гурвица с показателем пессимизма  и критерием Сэвиджа.

Вариант, №	Платёжная матрица	Показатель пессимизма 
1.		0,3
2.		0,8
3.		0,4
4.		0,6
5.		0,8
6.		0,7
7.		0,5
8.		0,9
9.		0,2
10.		0,1

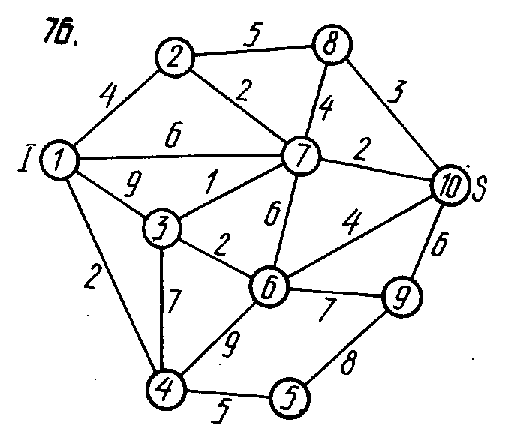
Задание 3. Задан граф, в котором известны длины рёбер. Требуется: 1) найти кратчайший путь из вершины I в вершину S методом построения всех путей; 2) найти максимальный путь из вершины I в вершину S методом динамического программирования на графе.

Вариант, №	Структура графа	Вариант, №	Структура графа
1.		6.
2.		7.
3.		8.
4.		9.
5.		10.