
6.5. Соотношение ар-, сс- и арсс-параметров
с автокорреляционной последовательностью
Этот раздел посвящен определению параметров модели в том случае, когда известна автокорреляционная последовательность. Если обе части уравнения (6.1) помножить на x* [n-m] и определить математическое ожидание, то получим
![]()
![]()
![]()
![]()
![]()
![]() (6.25)
(6.25)
или
![]() (6.26)
(6.26)
Взаимную корреляцию rux[i] между входом и выходом можно записать через параметры h[k], входящие в выражение (6.6), используя для этой цели уравнение (6.2),
что дает

![]() (6.27)
(6.27)
Поскольку полагается, что u[k] - белый шум, то
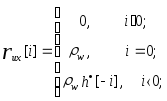 (6.28)
(6.28)![]()
Отсюда получаем окончательное выражение, связывающее параметры АРСС-модели и автокорреляционную последовательность процесса x[k]:
rxx[m]
=  (6.29)
(6.29)
где напомним читателю, что h[0] =1 по определению (см. уравнение (6.2)).
Авторегрессионные параметры АРСС-модели и автокорреляционная последовательность связаны системой линейных уравнений. Выражение (6.29) можно, например, записать для p значений индекса временного сдвига q+1 £ m £ q+p и затем представить в матричной форме
 (6.30)
(6.30)
Таким образом, если задана автокорреляционная последовательность для q-p+1 £ m £ q+p , то АР-параметры можно найти отдельно от СС-параметров как решение системы линейных уравнений (6.30). Уравнения (6.30) называются нормальными уравнениями Юла-Уолкера для АРСС-процесса; иногда их также называют модифицированными уравнениями Юла-Уолкера. Автокорреляционная матрица в системе (6.30) является тёплицевой, поэтому для решения этой системы можно применить подпрограмму, помещенную в приложении 3.Г. Количество требуемых для решения вычислительных операций пропорционально величине p2. Следует заметить, что значения СС-параметров АРСС-модели не являются, к сожалению, решением системы линейных уравнений. СС-параметры входят в выражение (6.29) в виде сверток с коэффициентами импульсной характеристики h[k], а это приводит к нелинейной связи автокорреляционной последовательностью.
Полагая в (6.29) q=0, получаем уравнение, связывающее авторегрессионную последовательность с параметрами авторегрессионной модели:
 (6.31)
(6.31)
Это выражение можно записать для p+1 значений индекса временного сдвига -0 £ m £ p и затем представить в матричной форме
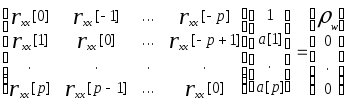 (6.32)
(6.32)
Таким
образом, если задана автокорреляционная
последовательность для 0
£
m
£
p
, то АР-параметры можно найти в результате
решения уравнений (6.32), которые называются
нормальными
уравнениями Юла-Уолкера для АР-процесса.
Автокорреляционная
матрица в (6.32) является тёплицевой, и
эрмитовой, поскольку
rxx[-k]
=
![]() .
Поэтому для получения решения pw
,
a[1],..., a[p] при
заданной АКП с 0
£
m
£
p
можно использовать подпрограмму LEVINSON
, помещенную в приложении 3.В. Количество
требуемых для этого вычислительных
операций пропорционально величине p2.
.
Поэтому для получения решения pw
,
a[1],..., a[p] при
заданной АКП с 0
£
m
£
p
можно использовать подпрограмму LEVINSON
, помещенную в приложении 3.В. Количество
требуемых для этого вычислительных
операций пропорционально величине p2.
Используя автокорреляционную последовательность, соответствующую уравнениям (6.31), получаем следующее выражение для СПМ авторегрессионного процесса:
 .
(6.33)
.
(6.33)
Заметим, что значения автокорреляции, соответствующие значениям индекса временного сдвига то 0 до p, однозначно описывают авторегрессионный процесс порядка p, поскольку значение автокорреляции при |k| > p получаются рекурсивно
![]() (6.34)
(6.34)
что следует из выражения (6.29) при q=0. Полагая в (6.29) p=0 и замечая, что h[k]= b[k] при 1 £ k £ q, получаем выражение, связывающее автокорреляционную последовательность с параметрами модели скользящего среднего
 (6.35)
(6.35)
Отсюда следует, что АКП и СС-параметры связаны нелинейным соотношением типа свертки. Используя далее автокорреляционную последовательность, соответствующую уравнениям (6.35), получаем выражение для СПМ процесса скользящего среднего
![]() (6.36)
(6.36)
Заметим, что суммирование в (6.36) осуществляется в конечных пределах, что просто отражает тот факт, что процесс скользящего среднего порядка q некоррелирован при временных сдвигах |k| > q. Выражение (6.36) идентично по форме выражению для оценки СПМ, получаемой с помощью классического коррелограммного метода:
![]() (6.37)
(6.37)
если
используются автокорреляционные оценки
![]() для
которых максимальное значение k
равно
q
. Различие между этими двумя методами
спектрального оценивания обусловлено
тем, как в них используются имеющиеся
данные. В коррелограммной методе данные
используются непосредственно для
получения оценки автокорреляционной
последовательности. В методе скользящего
среднего данные используются для
получения оценок СС-параметров (см.
гл.10, где описана процедура СС-оценивания),
а затем с помощью выражения (6.12) вычисляется
СПМ. Тем не менее оба метода дают спектры
с одинаковыми свойствами.
для
которых максимальное значение k
равно
q
. Различие между этими двумя методами
спектрального оценивания обусловлено
тем, как в них используются имеющиеся
данные. В коррелограммной методе данные
используются непосредственно для
получения оценки автокорреляционной
последовательности. В методе скользящего
среднего данные используются для
получения оценок СС-параметров (см.
гл.10, где описана процедура СС-оценивания),
а затем с помощью выражения (6.12) вычисляется
СПМ. Тем не менее оба метода дают спектры
с одинаковыми свойствами.
