6.4. Соотношения между параметрами

АР-, СС- и АРСС-моделей

Если задана АР-, СС- и АРСС-модель с конечным числом параметров, то ее можно представить через две другие модели. АРСС- и СС-процессы можно записать с помощью одной АР- модели в общем случае бесконечного порядка. Этот факт очень важен, так как позволяет выбирать любую из трех моделей и все же получать приемлемую аппроксимацию при достаточно большом порядке этой модели. Возможны определенные алгоритмические выгоды, если по имеющимся данным сначала оценить параметры какой-либо модели, а затем по ним вычислить значения параметров какой-либо другой модели. Много эффективных алгоритмов оценивания разработано, в частности, для АР- модели. Как будет показано в гл.10, оценивание параметров АР- модели большого порядка часто используется в качестве первого этапа алгоритма оценивания параметров СС- и АРСС-моделей.

Пусть

C(z) = 1 + (6.15)

- полином знаменателя АР(¥)-модели. Параметры c[k] АР(¥)-модели, которая эквивалентна АРСС (p, q )-модели, получаются из соотношения

(6.16)

или формированием обратного z-преобразования от C(z)B(z)= A(z). Отсюда получаем

c[n] = 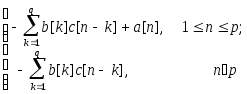(6.17)

с начальными условиями c[-1] =...= c[-q] = 0. И наоборот, если заданы параметры АР(¥)-модели, которая, как известно, эквивалентна АРСС (p, q )-модели, то значения СС-параметров можно восстановить, решая уравнение

(6.18)

относительно параметров b[k] и используя при этом соотношение (6.17) при Матрица параметров в уравнении (6.18) является тёплицевой, поэтому для его решения можно использовать подпрограмму TOEPLITZ , помещенную в приложении 3.Г. После определения СС-параметров значения АР-параметров АРСС-модели можно восстановить с помощью свертки

a[n] = c[n] + (6.19)

где Алгоритмы быстрой свертки основаны на использовании БПФ. Отметим также, что уравнение (6.19) выводится из уравнения (6.17).

Заметим, что в уравнениях (6.18) и (6.19) используются только авторегрессионные параметры c[1],...c[p+q] АР(¥)-модели. Если параметры c[k] при k>p+q полагаются равными нулю, то результирующая усеченная АР(p+q )-модель может аппроксимировать только ту АРСС(p+q )-модель, из которой она получена. Она аппроксимирует эту АРСС-модель в том смысле, что полином, обратный полиному АРСС-модели,

G(z) = (6.20)

и полином усеченной АР-модели

C(z) = 1+ (6.21)

согласованы, т.е. g[k] = c[k], только для .Эта аппроксимация рациональной функции полиномов конечного порядка полиномом более высокого порядка представляет собой известную задачу аппроксимации Паде . Эта процедура будет использована в гл.10 для вывода аппроксимаций АРСС-моделей высокого порядка. Типичные АР-аппроксимации высокого порядка для АРСС-модели низкого порядка показаны на рис.6.3.

Аналогичным образом пусть теперь

D(z) = 1+ (6.22)

- полином числителя СС()-модели. Параметрыb[k] этой модели, которая эквивалентна АРСС(p+q )-модели, можно определить, записывая уравнение

(6.23)

или формированием обратного -преобразования от D(z) A(z) = B(z). Отсюда получаем

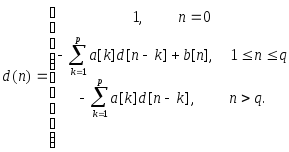(6.24)

Здесь также можно записать уравнения, аналогичные уравнениям (6.18) и (6.19). Типичные СС-аппроксимации для АРСС-модели показаны на рис.6.4.