§ .8 Формула Остроградского-Грина
Пусть
в плоскости xОy
задана область D,
ограниченная замкнутым контуром L,
а функции P(x;y)
и Q(x;y)
непрерывны вместе со своими частными
производными
и
в области D,
тогда справедлива формула:
@
где двойной интеграл берется по области D, а криволинейный интеграл вдоль замкнутого контура L, ограничивающего область D, в положительном направлении.
Доказательство:
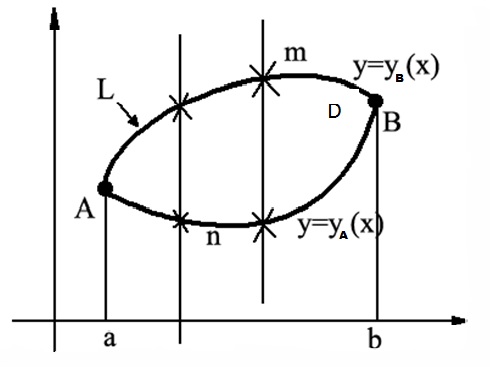Доказываем
формулу для случая, когда область D
такова, что прямые, параллельные осям
координат пересекают L
не более чем в 2-х точках.
y
D
=yA(x) – уравнение дуги AnBy=yB(x) – уравнение дуги AmB
Рассмотрим
Самостоятельно
доказать, что
.
Тогда
Замечания:
1. Формула остается справедливой и для областей, границы которых пересекаются прямыми, параллельные осям координат, более чем в 2-х точках.
2. @
3. Применение формулы Грина возможно только к криволинейным интегралам по @
§ .9 Независимость криволинейного интеграла II рода от пути интегрирования
В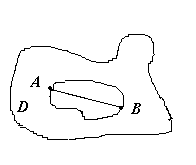
общем случае криволинейные интегралы
II
рода зависят
от пути
интегрирования,
но среди них существуют интегралы,
отвечающие специальным требованиям,
которые приводят к тому, что интегралы
не
зависят
от
пути интегрирования, а зависят лишь от
начальной и конечной точки.
Пусть A и B — две точки области D.
Рассмотрим различные линии,
лежащие в области D и соединяющие A и B.
Определение.
Если
по
любому из этих путей принимает одно и
то же значение, то говорят, что криволинейный
интеграл @
Теорема. Для того, чтобы криволинейный интеграл II рода в некоторой области D не зависел от пути интегрирования, необходимо и достаточно, чтобы
э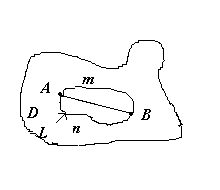
тот
интеграл, взятый по любому замкнутому
контуру, лежащему в области D, был равен
нулю.
Необходимость: Рассмотрим
произвольный контур L в обл. D и
возьмем на нём две произвольные точки
A и B.
Дано:
не зависит от пути интегрирования, т.е.
Доказать:
Доказательство:
Используя свойство о том, что при изменении направления пути интегрирования, криволинейный интеграл II-го рода меняет знак, получим
Достаточность: Пусть A и B - две произвольные точки области D. Соединим их произвольными кривыми AnB и AmB, которые образуют замкнутый контур L.
Дано:
Доказать: Криволинейный интеграл II рода не зависит от пути интегрирования, т.е.
Теорема доказана.
Итак, условие независимости криволинейного интеграла от пути интегрирования в некоторой области D равносильно тому, что @
Определение: Область D плоскости называется односвязной, если для любого замкнутого контура, лежащего в этой области, ограниченная им часть плоскости целиком принадлежит области D.
Задача:
Круг Прямоугольник
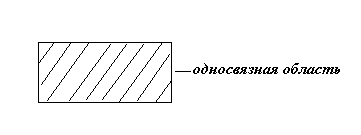
Кольцо
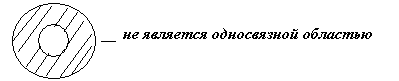
Теорема 2: Пусть функции P(x,y) и Q(x,y) непрерывны вместе со своими частными производными в односвязанной области D. Тогда для того, чтобы криволинейный интеграл по любому замкунтому контуру L, лежащему в области D, был равен нулю , т.е. не зависел от пути интегрирования, необходимо и достаточно, чтобы в каждой точке области D выполнялось условие
