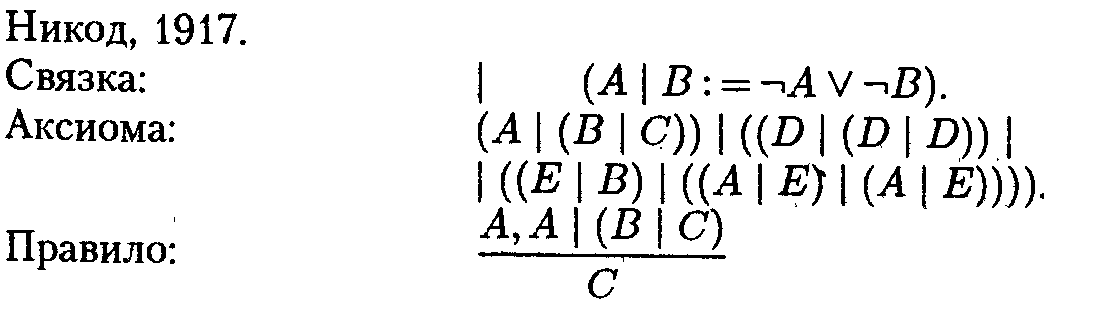3. Определение доказуемой формулы.

а) Всякая аксиома является доказуемой формулой.

б) Формула, полученная из доказуемой формулы путем применения подстановки вместо переменной х произвольной формулы В есть доказуемая формула.

в) Формула В. полученная из доказуемых формул А и А В путем применения правила заключения, есть доказуемая формула.

г) Никакая другая формула исчисления высказываний не считается доказуемой.

Процесс получения доказуемых формул будем называть доказательством.

Приведем примеры доказательств.

1. Доказать, что A  А (рефлективность импликации).

Воспользуемся аксиомой I2:

И выполним подстановку вместо переменной z формулы В=х Тоrда получим

(1)

Применяя правило заключения к аксиоме I1 и формуле (1). получим

. (2)

В формуле (2) осуществим подстановку вместо переменной y подставим

в результате получим доказуемую формулу

. (3)

Применим правило заключения к аксиоме IV 3 и формуле (3). Это приводит к доказуемой формуле x х.

Наконец, осуществив подстановку в формуле (4) вместо х формулы А. получим AA.

Докажите самостоятельно:

4. Производные правила вывода

Производные правила вывода. как и рассмотренные правила подстановки и заключения, позволяют получать новые доказуемые формулы. Они получаются с помощью правил подстановки и заключения, а поэтому являются производными от них.

1. Правило одновременной подстановки.

Пусть А - доказуемая формула; x₁ , х₂ . ..., х_n - переменные. а B_l, В₂, .... В_n- любые формулы исчисления

высказываний. Тогда результат одновременной подстановки в А вместо x₁ , х₂ . .... х_n соответственно формул B_l, В₂ ..., В_n является доказуемой формулой.

Схематично операция одновременной подстановки записывается в виде:

2. Правило сложного заключения.

Второе производное правило применяется к формулам вида

и формулируется так:

Если формулы А₁ , А₂, ..., А_n и доказуемы, то и

формула L доказуема.

Правило сложного заключения схематично записывается так:

3. Правило силлогизма.

Если доказуемы формулы А  В и В С, то доказуема формула А С.

Для доказательства этого правила сделаем следующие одновременные подстановки:

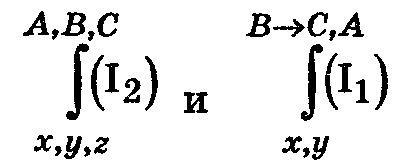
Получим доказуемые формулы

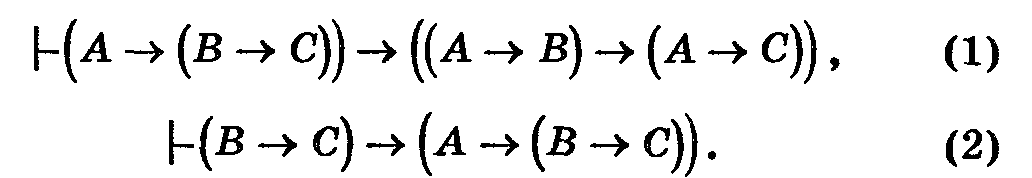
По условию, доказуемыми будут формулы:

Из (2) и (4) по ПЗ получаем

Из (5), (3), (1) по ПСЗ получаем

4. Правило контрпозиции.

5. Правило снятия двойного отрицания.

а) Если доказуема формула , то доказуема формула AB .

б) Если доказуема формула . то доказуема формула А В .

Доказательство 4 и 5 пункта выполнить самостоятельно.

Лекция 6

Доказательство некоторых законов алгебры логики.

Из закона перестановки посылок вытекает правило перестановки посылок , которое применяется при выводе заключения:

На практике в большей мере используется правило перестановки посылок:

Правило разъединения посылок имеет вид:

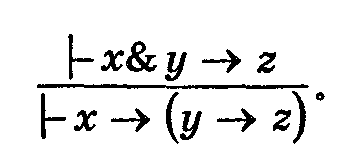
Доказательство. Сделаем подстановки в аксиомы I1 и IV 1

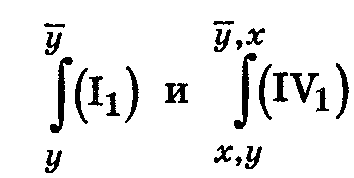
В результате получим доказуемые формулы (1) и (2).

Из формул (1) и (2) по ПС следует

Применяя к этой формуле правило соединения посылок получим:

Используя ПСДО , получим .

Применяя правило разъединения посылок получаем формулу

V. Закон исключенного третьего :

Доказательство. Воспользуемся доказуемой формулой (3)

Сделав в ней подстановку , получим доказуемую формулу (5)

В формуле (4) сделаем подстановку: x заменим x на , y на y.

В результате получим формулу: . Применяя к ней правило соединения посылок, получим:

.(6). Из (5) и (6) по ПС получаем , применяя ПК к данной формуле получим: .

По ПСДО .

Подставив вместо y любую доказуемую формулу и применяя правило подстановки получим .

Доказать самостоятельно.

Другие аксиоматизации исчисления высказываний

Рассмотренная теория не является единственной возможной аксиоматизацией исчисления высказываний.

Известны и многие другие аксиоматизации исчисления высказываний, предложенные различными авторами.

3.