
- •Задачи к практическим занятиям по дисциплине «Проектный анализ»
- •1. Ситуация:
- •6. Задача.
- •7. Задача:
- •17. Задача
- •20. Задача
- •21.Задача
- •Примеры задач из книги
- •4. Финансово-математические основы инвестиционного проектирования
- •Вопрос 1.
- •Вопрос 2.
- •Вопрос 3.
- •Вопрос 4.
- •Задания.
- •5. Оценка стоимости ценных бумаг предприятия и составление графиков возврата долгосрочных кредитов
- •6. Оценка стоимости капитала инвестиционного проекта
- •Задания
- •7. Основные критерии эффективности инвестиционного проекта и методы их оценки
- •7. Сравнение npv и irr методов
- •8. Анализ безубыточности и целевое планирование прибыли в процессе инвестиционного проектирования
Номінальна вартість (номінал акції) — ціна, вказана на бланку акції. Вона характеризує частку статутного капіталу, яка припадає на одну акцію під час заснування компанії.
Емісійна вартість — ціна, за якою акція реалізується (продається) на первинному ринку; може відрізнятися від номіналу.
Балансова вартість — величина власного капіталу, що припадає на одну акцію. Якщо емітовано лише прості акції, то така вартість визначається діленням власного капіталу на кількість акцій. Якщо випущено й привілейовані акції, то власний капітал зменшується на сукупну вартість привілейованих акцій за номіналом або за викупною ціною (для відзивних акцій).
Ринкова вартість (або курсова вартість) — ціна, за якою акції продаються та купуються на ринку; саме за цією ціною акції котируються на вторинному ринку цінних паперів.
Курс акції— відношення ринкової ціни до номіналу, виражене у процентах.
Ліквідаційна вартість — визначається в момент ліквідації акціонерного товариства. Вона показує, якою є вартість майна акціонерного товариства, що припадає на одну акцію і підлягає реалізації у фактичних цінах після розрахунку з кредиторами.
У деяких країнах акціонерні товариства емітують відзивні привілейовані акції. У такому разі емітент має право «відкликати» акції шляхом викупу їх у певний момент за відповідною ціною — ціною викупу (саll ргісе).
Також емітуються конверсійні привілейовані акції, які в певний період часу можна обміняти на прості акції за заздалегідь встановленим курсом (конверсійною ціною).
Оцінка поточної вартості привілейованих акцій пов'язана з приведенням доходів (фіксованих дивідендів) до поточної вартості і фактично може бути визначена за формулою
![]()
де Ра— поточна ринкова вартість акцій;
D — річна сума постійних дивідендів:
r — норма дохідності акцій подібного класу ризику (десятковий дріб).
Таким чином, найпростішим варіантом оцінки поточної вартості привілейованих акцій є співвідношення величини дивідендів та ринкової норми дохідності за акціями подібного класу ризику.
У деяких випадках відбувається емісія привілейованих акцій на умовах їх викупу в певний момент за відповідною ціною — ціною викупу. Тоді поточна ринкова вартість визначається за формулою
![]()
де Pm —Ціна викупу акції;
п — кількість років використання акції.
Для спеціалістів фондового ринку важливою задачею є визначення вартості простих акцій, оскільки вони не мають гарантованого рівня доходів. Як відомо, доходами за акціями є дивіденди та капітальний приріст вартості акцій. Майбутні грошові потоки за простими акціями можуть складатися із суми нарахованих дивідендів — якщо акції використовуватимуться протягом невизначеного періоду часу, або із суми нарахованих дивідендів і прогнозної вартості реалізації фондового інструменту — якщо акції використовуватимуться протягом заздалегідь обумовленого періоду часу.
У разі оцінювання поточної вартості простих акцій використовуються такі три варіанти прогнозування динаміки дивідендів:
а) дивіденди не змінюються — темп приросту дорівнює нулю;
б) дивіденди зростають з постійним темпом приросту;
в) дивіденди зростають зі змінним темпом приросту.
За умови постійних виплат дивідендів поточна ринкова вартість простих акцій визначається як і з привілейованих акцій, тобто:
![]()
Де Ра— поточна ринкова вартість акцій;
D — річна сума дивідендів;
r — норма дохідності акцій подібного класу ризику (десятковий дріб).
Приклад 1
Компанія сплачує річні дивіденди в розмірі 17 грн. на акцію, норма поточної дохідності за акціями даного типу становить 14 %. Яка має бути вартість акції?
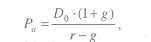
![]()
Для розрахунку поточної вартості акцій з постійним приростом дивідендів використовується так звана «модель Гордона»:
де g — річний темп приросту дивідендів, (десятковий дріб);
g = const.
Dо — дивіденди, сплачені компанією протягом року. Ця формула g < r.
Приклад 2
Компанія протягом року виплатила дивіденди в розмірі 15 грн. на акцію.
![]()
![]()
Щорічно дивідендні виплати зростають на 12,6 %, норма поточної дохідності за акціями даного типу становить 14 %. Яка має бути вартість акції?
де Di — обсяг дивідендів, які інвестор прогнозує отримати в i-му периоде:
Приклад 3
Підприємство виплатило за останній рік дивіденди в розмірі 0,24 грн. на акцію. Протягом другого року воно планує збільшити дивіденди на 3 %, третього — на 7 %, у подальшому планується постійне зростання дивідендів на 8 % річних. Необхідно оцінити вартість акції за умови, що норма дохідності акцій даного типу становить 12 %.
У даній задачі підприємство точніше визначає дивідендні виплати за перші три роки та здійснює прогноз постійного приросту дивідендів у безмежному періоді часу з урахуванням g (річного темпу приросту дивідендів). У подальшому оцінка поточної ринкової вар-| тості акцій визначається дисконтуванням спрогнозованої сукупності дивідендів. Формула оцінки вартості акцій може мати такий вигляд: і
![]()
Спочатку визначимо рівень дивідендів, які сплачуютьея в перші три роки:
D1 =0,24;
![]()
У наступні роки підприємство планує щорічне збільшення дивідендів на 8 %, тому для визначення вартості акції використаємо формулу (4):
![]()
Оскільки показник Р2 дає оцінку вартості акції на кінець третього періоду, а необхідно знайти поточну вартість на початок першого періоду, здійснюється дисконтування:
![]()
Інвестори не завжди мають в своєму портфелі постійні обсяги і види певних фінансових інструментів; під впливом цілей інвестування відбувається зміна цінних паперів. Коли інвестор заздалегідь прогнозує термін використання певних акцій, їх поточна ринкова вартість може бути оцінена за формулою
![]()
де О, — обсяг дивідендів, які інвестор прогнозує отримати у t-му періоді;
Рr — прогнозна вартість реалізації акцій в кінці періоду її використання;
п — кількість періодів використання акції.
Для визначення вартості акцій застосовується й модифікована модель, яка враховує прибуток підприємства та напрями його використання:
![]()
Де I — очікуваний прибуток наступного року;
b — частка прибутку, спрямованого на інвестування;
r— норма дохідності акцій даного типу (десятковий дріб);
k — дохідність вкладень в розвиток фірми (десятковий дріб).
Приклад 4
Інвестор прогнозує, що в наступному році компанія отримає прибуток у розмірі 17 грн. на акцію. Частка прибутку, спрямованого на реінвестування, становить 60 %, необхідний рівень дохідності — 14 %. Прибуток, спрямований на розвиток виpобництва, забезпечує отримання доходу в розмірі 18%.
![]()
Оцінка вартості акцій показує, що коли на ринку акції котируються за ціною, нижчою 212,5 грн., то вони недооцінені і є сенс вкладати в та кошти, у противному разі, відповідно, акції є переоціненими і придбання їх не має сенсу.
Дохідність характеризує рівень доходу, який генерується фінансовим активом на одиницю інвестованих у даний актив коштів. У ролі доходів за фінансовими інструментами можуть виступати дивіденди, проценти, приріст капіталізованої вартості. Аналізуючи фінансові інвестиції можна розрахувати очікувану й фактичну дохідність. Для інвестора в процесі прийняття рішення про доцільність вкладень важливим є розрахунок очікуваної дохідності на основі прогнозних даних.
Для аналізу ефективності операцій з акціями використовуються такі показники: ставка дивіденду, поточна ринкова дохідність, поточна дохідність акції для інвестора, сукупна (повна) дохідність.
Ставка дивіденду (Дд) визначається за формулою
![]()
де D — очікувані річні дивіденди, грн.;
N — номінальна вартість, грн.
![]()
де Рa — поточна ринкова вартість акцій, грн.
Поточна дохідність акцій для інвестора (Дп) — рендит розраховується як співвідношення обсягу річних дивідендів і вартості придбання акції:
![]()
У разі прийняття рішення про доцільність придбання акції на основі рівня поточної дохідності інвестор, як правило, прогнозує довгострокові інвестиції в цей фінансовий актив. Тому сукупна дохідність у цьому разі, збігається з поточною дивідендною дохідністю.
За купівлі акцій з метою перепродажу через деякий час ураховуються дивідендна і капіталізована дохідність. Отже, сукупна (повна) дохідність може бути визначена за формулою
![]()
де Di — річні дивіденди, які виплачуються в і-му році;
Рt — ринкова вартість акцій у t-му році;
Р0 — вартість придбання акцій.
Середньорічна сукупна дохідність (кінцева дохідність) за акціями визначається за формулою
![]()
Приклад 5
Інвестор придбав акцію номіналом 30 грн. за курсом 117 % і продав її через 4 роки за курсом 136 %. У перший рік рівень дивідендів становив 2,4 грн. на акцію, у другий рік ставка дивіденду становила 10 %, у третій — 11 %, у четвертий рік рівень дивідендів становив 3,4 грн. Розрахуйте сукупну дохідність і середньорічну (кінцеву) дохідність акції.
Дивіденди становили:
рік—> 2,4 грн.;
рік-> 30 грн. * 0,1 = 3 грн.; 3 рік-> 30 грн.* 0,11 =3,3 грн.;
4 рік—> 3,4 грн.;
Ро = 30 *1,17 = 35,1 (грн.);
Р1 = 30 * 1,36 = 40,8 (грн.).
Для розрахунку сукупної дохідності використовуємо формулу (11):
![]()
Для визначення кінцевої дохідності — формулу (12):
![]()
Середньорічна сукупна дохідність (кінцева) за короткостроковими операціями може бути розрахована за формулою
![]()
Приклад 6
Інвестор придбав акції ВАТ «Шелл» 18 вересня 2000 р. за ціною 25,6 грн., продав їх 25 березня 2001 р. за ціною 27,2 грн.; 15 лютого він отримав дивіденди в розмірі 1,6 грн. на акцію. Визначте середньорічну сукупну дохідність акції.
Період володіння акціями (Т) = 12 + 31 + 30 + 31 + 31 + 28 + + 25 = 188 (дн.).
![]()
Визначення вартості та оцінка фективності операцій з облігаціями і депозитними сертифікатами
Суть оцінки вартості облігації полягає в тому, що протягом періоду обігу облігації її власник має отримати ту саму суму, яку він уклав в облігацію, купуючи її. Проте сукупність платежів, які має отримати власник облігацій, розтягнуто у часі, і відповідно всі майбутні платежі необхідно привести до теперішньої вартості (моменту часу, на який здійснюється оцінювання) шляхом дисконтування.
Сума майбутніх грошових потоків за купонними облігаціями складається з процентів за фінансовим активом і ціни облігації на момент погашення. За оцінювання вартості купонної облігації враховуються такі показники: номінальна вартість, процентна ставка, строк до погашення, умови виплати процентів (періодичність виплат). Отже, поточна ринкова вартість купонних облігацій за умови, що протягом строку обігу облігації здійснюються періодичні виплати процентів, а в кінці строку виплачується номінал, розраховується за формулою
![]()
Де Робл — поточна вартість облігації з періодичною виплатою процентів;
С — річні купонні виплати;
N— номінальна вартість облігації;
r — ринкова процентна ставка в «-му періоді (дохідність в альтернативному секторі);
і — кількість періодів, протягом яких здійснюються купонні виплати.
Ця формула є базовою математичною моделлю оцінки грошової вартості процентних облігацій.
Приклад 7
Визначте вартість облігації, випущеної на 10 років, до погашення залишилося 4 роки. Номінальна вартість — 200 грн., річна купонна ставка — 18 %, ринкова дохідність (ставка дисконтування)—12%.
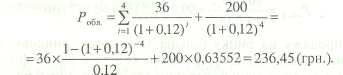
Поточна ринкова вартість облігації становить 236,448 грн. У разі виплати суми купону за облігаціями частіше за один раз на рік формулу (14) можна трансформувати у формулу
![]()
де k — періодичність виплати процентів протягом року.
Приклад 8
На ринку пропонується облігація номіналом 200 грн., купонною ставкою 18% річних і строком погашення через 4 роки. Ринкова дохідність фінансових інструментів такого класу становить 12 %. Процент за облігацією сплачується тричі на рік, необхідно розрахувати поточну ринкову вартість облігації.
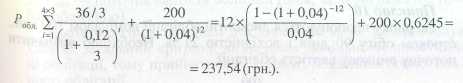
У цьому прикладі вартість облігації вища, ніж у прикладі 10, оскільки процентні платежі інвестор отримує частіше. Ціна, за якою доцільно купувати облігацію, — 237,54 грн.
У разі виплати всієї суми процентів під час погашення облігації формула (14) модифікується у формулу
![]()
де Сk — сума процентів за облігацією, яку буде нараховано під час її погашення за відповідною ставкою.
Приклад 9
Облігація підприємства «Форум» номіналом 80 гри. реалізується на ринку за ціною 60 грн. Погашення облігації і виплату процентів передбачено через 4 роки. Процентна ставка — 24 % річних, норма поточної дохідності за облігаціями такого типу — 18 %. Необхідно визначити поточну ринкову вартість облігації
![]()
Ціна продажу на ринку більша за поточну ринкову вартість (51,17 грн.), отже, інвестор, вклавши кошти в даний фінансовий інструмент, матиме меншу поточну дохідність, ніж у разі альтернативного розміщення коштів.
Для облігацій з нульовим купоном (дисконтних) поточна ринкова вартість визначається за формулою
![]()
де п — кількість років, через які відбудеться погашення облігації. Якщо строк обігу дисконтних облігацій менший одного року, то поточна ринкова вартість облігації визначається за формулою
![]()
де Т— кількість днів до погашення облігації.
Приклад 10
На ринку пропонуються дисконтні облігації номіналом 100 гри., строком обігу 90 днів і дохідністю 21 %. Необхідно визначити поточну ринкову вартість облігації.
![]()
![]()
і фактично являє собою суму членів нескінченно спадної геометричної прогресії.
Для оцінки ефективності вкладень в облігації використовують такі показники: купонна, поточна і повна дохідність.
1. Купонна ставка (Де) — установлюється у разі емісії облігації, визначається відносно номіналу і показує, який процент доходу нараховується щорічно власникові облігації. Купонна ставка визначається за формулою
![]()
де С — річний купонний дохід, грош. од.
Як правило, цей показник не розраховується, а встановлюється згідно з умовами випуску.
2. Поточна дохідність — визначає процент доходу, який щорічно отримує власник облігації на інвестований капітал. Розраховується як процентне співвідношення між річним купонним доходом від облігації і тією ціною, за якою інвестор ії придбав.
Слід розрізняти дохідність, яка наводиться у біржових зведеннях, і дохідність для певного інвестора: у першому випадку у знаменнику стоїть поточна вартість цінного паперу, в другому — використовується ціна, за якою інвестор купив облігацію. Отже, поточна дохідність може бути визначена за формулою
![]()
Де Робл — поточна вартість облігації (ціна, за якою інвестор придбав облігацію).
Проте показник поточної дохідності не може використовуватися як загальний критерій визначення доцільності інвестицій в ці облігації, тому прийнятнішим є аналіз показника повної дохідності облігації.
3. Дохідність до дати погашення (кінцева дохідність облігації)— характеризує не тільки поточний дохід за облігацією, а й виграш (збиток), який отримує інвестор, погашаючи облігацію за ціною, вищою або нижчою за ціну купівлі. Повна дохідність розраховується за формулою
![]()
де Р1 — вартість реалізації (номінал) облігації;
Р0 — ціна купівлі облігації (поточна вартість на момент оцінки); п — кількість років обігу облігації.
Приклад 11
На ринку реалізуються облігації кількох емітентів: облігації «SРС» з номіналом 100 гри. і купонною ставкою 22 % річних реалізуються за курсом 107 %, строк до погашення 3 роки; облігації «Крам» з номіналом 80 гри. та купонною ставкою 18 % річних реалізується за курсом 92 %, строк до погашення 2 роки; облігації «Аква» реалізуються за номіналом в 90 гри., мають купонну ставку 20 %; строк до погашення — 2 роки.
Яку з облігацій купить інвестор, ураховуючи рівень доходу кожного фінансового активу?
Облігації «SРС» -> Ркуп = 107 грн.
Облігації «Крам» —> Ркуп = 73,6 грн.
Облігації «Аква» —> Ркуп = 90 грн
![]()
![]()
![]()
Для інвестора, метою якого є максимізація доходів, доцільним є вкладання коштів в облігації «Крам».
Модель розрахунку очікуваної поточної дохідності за облігаціями з виплатою всієї суми процентів під час погашення випливає з рівняння (16) і визначається
![]()
Приклад 12
За даними прикладу 9 очікувана поточна дохідність за облігаціями підприємства «Форум» становить
![]()
Фактично ми підтвердили висновки про недоцільність придбання цих облігацій, оскільки, по-перше, ціна продажу на ринку більша за розрахункову вартість облігації і, по-друге, поточна дохідність за облігацією (13,39 %) менша альтернативного рівня дохідності (18 %).
Очікувана дохідність за дисконтними облігаціями (з нульовим купоном) випливає з формули (16) і визначається як:
![]()
Приклад 13
Облігація з нульовим купоном номіналом 150 гри. і строком погашення через 3 роки реалізується за ціною 98 грн. Проаналізуйте доцільність придбання цієї облігації, якщо є можливість альтернативного інвестування з нормою дохідності 14 %.
![]()
Розрахунок показує, що придбання облігації є доцільним, оскільки дохідність облігації (15,25 %) більша за норму альтернативної дохідності (14 %).
Для аналізу також можна розрахувати теоретичну вартість облігації і порівняти її з поточною ціною на ринку. Для цього скористаємося формулою (17):
![]()
Оскільки інвестор може купити облігацію за ціною, нижчою за розрахункову теоретичну вартість, то він зможе отримати дохідність, вищу за 14 %. Отже, вкладання коштів в цю облігацію має сенс.
На ринку також розміщуються короткострокові дисконтні облігації (строк обігу менше одного року). У такому разі очікувану дохідність можна розрахувати за формулою
![]()
де N— ціна погашення облігації (номінал);
Ркуп — ціна купівлі облігації;
Т — кількість днів між купівлею і продажем облігації (кількість днів з дня розміщення до дня погашення).
Як вже зазначалося за розрахунку поточної ринкової вартості облігації, на ринку розміщуються й безстрокові облігації, за якими виплачується фіксований купон протягом строку обігу фінансового активу. В такому разі модель розрахунку очікуваної поточної дохідності може мати вигляд:
![]()
де Робл — ціна, за якою облігація реалізується на ринку.
Приклад 14
Облігація фірми «ДЕСК» номіналом 250 гри. реалізується на ринку за ціною 300 грн. Купонна ставка (щорічна) становить 22 %. Норма поточної дохідності за облігаціями такого типу — 20 %. Необхідно визначити очікувану поточну дохідність за облігацією та проаналізувати доцільність інвестицій
![]()
Дохідність облігації (18,3 %) менша за норму альтернативної дохідності на ринку (20 %), тому придбання облігації фірми «ДЕСК» є невигідним розміщенням капіталу.
Задачи к практическим занятиям по дисциплине «Проектный анализ»
1. Ситуация:
Предприятие начинает производить новое оборудование для сахарной промышленности. Это оборудование более долговечно, чем имеющиеся на рынке. Известно, что в течение года на рынок поступит подобное оборудование.
Сформулируйте цель предприятия.
Анализ целей:
Предприятие будет заинтересовано в быстром насыщении рынка и в росте сбыта для занятия доминирующего положения на рынке долговечного оборудования . Доминирующее положение – основа для контроля рынка в дальнейшем и получении стабильного дохода.
Формулировка цели:
Максимизация сбыта. Данную цель можно сформулировать и как достижение определённой доли рынка. Допустим, изменение доли на рынке с 10% до 25% за три года»
2. Задача
По данным таблицы сделайте анализ по эффективности проектов в зависимости от нормы дисконта.
Норма дисконта |
15 |
20 |
25 |
2.ИД для первого проекта
3.ИД для второго проекта |
1,4067
1,4085 |
1,2998
1,3145 |
0,9465
1,067 |
Как видно из таблицы, эффективность проектов один и два при ставке нормы дисконта в 15% примерно одинакова. При индексе доходности больше единицы (ИД>1) проект признаётся эффективным и наоборот.
3. Задача
По проекту «А» сумма чистого денежного потока составляет 5500 грн., объём инвестиционных средств – 4500 грн. По проекту «Б» - соответственно 7000 грн. и 6000 грн. Какой из инвестиционных проектов по «индексу доходности» является более эффективным?
Индекс доходности определяется как отношение чистого денежного потока к объему инвестиционных средств (Формула (1).
ИД = ЧПи / ИС
Задача
Необходимо определить будущую стоимость выхода за весь период инвестирования, если первоначальная стоимость выхода 1000 грн.; процентная ставка, используемая при расчёте суммы сложного процента, установлена в размере 20% в квартале.
Подставляя эти показатели в нижеприведённую формулу, получим:
Sc = P×(1+i)n , где Sc – будущая стоимость выхода (денежных средств, при его наращении по сложным процентам);
Р – первоначальная сумма вклада;
i – используемая процентная ставка, выраженная десятичной дробью;
n – кол-во интервалов, по которым осуществляется каждый % платёж в общем периоде времени (год).
Задача
Сколько денег надо инвестировать сейчас, чтобы через 2 года получить 100 тыс. грн., при доходности 10% годовых?
Сn =Сб/(1+Е)t (1),
где Сn – сегодняшняя стоимость будущих денег;
Сб – будущая стоимость сегодняшних денег;
Е – норма дохода на капитал, выраженная десятичной дробью;
t - время в годах или в месяцах
6. Задача.
Необходимо определить годовой темп инфляции, если в соответствии с прогнозом экономического и социального развития страны ожидаемый среднемесячный темп инфляции определён в размере 3%.
Используем формулу (1)
Тиг=(1+Тим)12,
где Тиг - прогнозируемый годовой темп инфляции, выраженный десятичной дробью
Тим -ожидаемый среднемесячный темп инфляции в предстоящем периоде, выраженный десятичной дробью.
