2.3Розрахунок коефіцієнтів кореляції і детермінації, перевірка правильності обраних факторів та форми зв'язку
Ми з'ясували можливість встановлення кореляційного зв'язку між значеннями х і відповідними значеннями у. Тепер необхідно з'ясувати, як зміна факторного ознаки впливає на зміну результативної ознаки.
Обчислимо коефіцієнта кореляції за формулою (3) для розрахунку лінійного коефіцієнта кореляції:
(3)
Отримаємо:
Лінійний коефіцієнт кореляції може приймати будь-які значення в межах від мінус 1 до плюс 1. Чим ближче коефіцієнт кореляції за абсолютною величиною до 1, тим тісніше зв'язок між ознаками. Знак при лінійному коефіцієнті кореляції вказує на напрям зв'язку - прямій залежності відповідає знак плюс, а зворотної залежності - знак мінус.
У нашому прикладі r = 0,990.
Крім того, можна розрахувати коефіцієнт детермінації d , який дорівнює квадрату коефіцієнта кореляції.
У нашому прикладі d = 0,981.
Це означає, що зміна витрат на товар А можна на 98,1% пояснити зміною доходу.
Решта 1,9% можуть бути наслідком:
недостатньо добре підібраною формою зв'язку;
впливу на залежну змінну будь-яких інших неврахованих факторів.
Доцільно перевірити, чи не покращиться результат, якщо взяти криволінійну форму зв'язку.
Скористаємося статечної функцією виду: ŷ = AX B
Логарифмуємо:
lg ŷ = lga + blgx. (4)
2
4,07
= 11*a + 28,85*b, => а=
63,26 = 28,85*a + 75,98*b
63,26 = 28,85 ( ) + 75,98*b,
0,1282 = 0,31*b, => b = 0,4092
а
=
lg у = 1,1149 + 0,4092 lgх
Для знаходження параметрів а і b всю процедуру МНК проробляємо не з величинами у і х , а з їх логарифмами. Після розв'язання системи нормальних рівнянь (2) отримуємо: LG A = 1,1149; b = 0,4092.
Рівняння регресії: LG ŷ = 1,1149 + 0,4092 LG X
Порівняємо фактичні та розрахункові витрати на споживання товару А (таблиця 3) і побудуємо графік отриманої функції ŷ (рисунок 2).
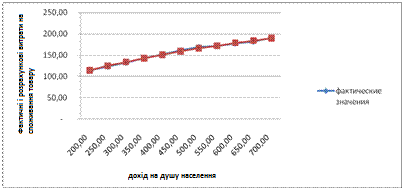
Рисунок 2 Порівняння фактичних і розрахункових витрат на споживання товару А для степеневого рівняння регресії
Таблиця 3. Порівняння фактичних і розрахункових значень витрат на споживання товару А при ступеневій залежності
№ групи |
Витрати на товар А |
Відхилення фактичних значень від розрахункових (у-ŷ) |
||
фактичні (у) |
Розрахункові ( ŷ ) |
абсолютні |
відносні (у відсотках) |
|
1 |
114,00 |
114,00 |
- |
0% |
2 |
123,00 |
125,00 |
- 2,00 |
-2% |
3 |
132,00 |
134,00 |
- 2,00 |
-2% |
4 |
143,00 |
143,00 |
- |
0% |
5 |
152,00 |
151,00 |
1,00 |
1% |
6 |
161,00 |
159,00 |
2,00 |
1% |
7 |
169,00 |
166,00 |
3,00 |
2% |
8 |
171,00 |
172,00 |
- 1,00 |
-1% |
9 |
178,00 |
179,00 |
- 1,00 |
-1% |
10 |
182,00 |
184,00 |
- 2,00 |
-1% |
11 |
191,00 |
190,00 |
1,00 |
1% |
Всього |
- |
- |
- 1,00 |
- |
Тіснота криволінійної зв'язку вимірюється кореляційним відношенням, позначається через і мають таке ж значення, що і r .
Теоретичне кореляційне відношення може бути розраховано за формулою:
= , (5)
де 2 фактор -дисперсія для теоретичних значень ŷ (пояснена варіація);
2 заг - дисперсія для фактичних значень у (непояснена варіація).
= 
= 
=
0,978
У нашому прикладі = 0,978 , ² = 0,958.
Як бачимо, степенева форма зв'язку точніше відображає залежність споживання товару А від доходу.