Теория np-полноты Труднорешаемые задачи

Рассмотренные ранее алгоритмы были полиномиальными.

Полиномиальным алгоритмом (или алгоритмом полиномиальной временной сложности) называется алгоритм, временная сложность которого равна O(p(n)), где p(n) – некоторая полиномиальная функция, а n – входная длина.

Множество полиномиальных алгоритмов образует класс полиномиальных алгоритмов – класс Р.

Всякая ли задача может быть решена за полиномиальное время? Ответ отрицательный, так как существуют вообще неразрешимые задачи, и есть задачи разрешимые, но за более чем полиномиальное время. Примеры:

1. Решение задачи об укладке рюкзака. При условии, что каждый из n предметов может быть упакован или не упакован в рюкзак, всего будет 2ⁿ вариантов взятых предметов.

2. Решение задачи коммивояжера сводится в худшем случае к перебору всех возможных маршрутов, а их всего существует (n-1)!. Это зависимость не может быть выражена полиномиальной функцией, причем можно заметить, что n≥2ⁿ

Задачи, для решения которых не существует полиномиального алгоритма, но существует экспоненциальный алгоритм (O(aⁿ)), называют труднорешаемыми.

Отличие полиномиальных и экспоненциальных алгоритмов будет более ощутимо, если обратиться к таблице, в которой отображено время работы алгоритма на компьютере, выполняющем 1000000 оп/с:

n O(n)	10	20	30	40	50	60
n	0.00001 c	0.00002 c	0.00003 c	0.00004 c	0.00005 c	0.00006 c
n2	0.0001 c	0.0004 c	0.0009 c	0.0016 c	0.0025 c	0.0036 c
n5	0.1 c	3.2 c	24.3 c	1.7 мин	5.2 мин	13 мин
2n	0.001 c	1 c	17.9 мин	12.7 дней	35.7 лет	366 столет.
3n	0.059 c	58 мин	6.5 лет	3855 стол.	2∙108 стол.	1.3∙1013ст.
n!	3.6 c	771,5 стол.	8∙1016стол	…	…	…

Таким образом, понятие полиномиально разрешимой задачи принято считать уточнением идеи «практически разрешимой» задачи:

1. Полиномиальные алгоритмы действительно работают быстро, а полиномы больших степеней (n¹⁰⁰) и полиномы с большим коэффициентом пропорциональности (10⁹⁹·n^a) на практике встречаются крайне редко.

2. Полиномиальные алгоритмы не зависят от выбора конкретной модели вычислений (P_{по Тьюрингу}= P_{на МПД}= P _{для параллельных вычислений}).

3. Класс Р обладает свойством замкнутости (композиция двух полиномиальных алгоритмов дает алгоритм также полиномиальный, так как сумма, произведение и композиция многочленов, тоже являются многочленами).

Нерешенные проблемы теории np-полноты

К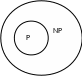 ак соотносятся классы P и NP? Так как любая задача класса Р проверяема за полиномиальное время, то очевидно следующее включение.

Однако не известно, совпадают ли классы P и NP, но большинство специалистов считает, что нет. Интуитивно класс Р можно представить себе как класс задач, которые можно быстро решить, а класс NP – как класс задач, решение которых можно быстро проверить.

Существуют и другие открытые вопросы относительно класса NP:

1. Вопрос эквивалентности классов P и NP.

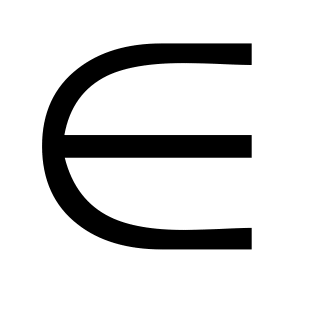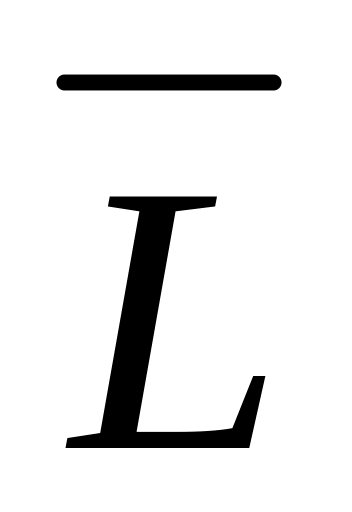2. Вопрос замкнутости класса NP относительно дополнения, т. е. верно ли, что если L NP, то и NP. Множество всех задач L, для которых это условие выполняется, назовем классом co-NP.

Так как класс Р замкнут относительно дополнения, то возможны следующие соотношения классов.