
Глава 17
Программирование второго порядка
В гл. 14и 15были рассмотрены методы программирования на Прологе, основанные непосредственно на логическом программировании. В этой главе программирование на Прологе расширяется введением методов, отсутствующих и модели логического программирования. Эти методы основаны на свойствах языка, выходящих за рамки логики первого порядка. Они названыметодами второго порядка,поскольку речь здесь идет о множествах и их свойствах, а не об отдельных элементах.
В первом разделе вводятся множественные предикаты, которые в качестве решений вырабатывают множества. Вычисления с использованием множественных выражений приобретают особую силу. когда применяются в сочетании с уже рассмотренными методами программирования. Второй раздел посвящен некоторым приложениям множественных предикатов. В третьем разделе обсуждаются лямбда -выражения и предикатные переменные, которые позволяют рассматривать функции и отношения как «первоклассные» объекты данных.
17.1. Множественные выражения
Решение какого-либо вопроса в программе на Прологе вызывает поиск некоторого примера вопроса, выводимого из программы. Что произойдет, если осуществлять поиск всех примеров вопроса, выводимых из программы? На декларативном уровне такой вопрос лежит вне модели логического программирования, представленной в гл. 1.Это вопрос второго порядка, поскольку он касается множества элементов с определенными свойствами. В случае операционного толкования он выходит и за рамки вычислительной модели чистого Пролога. В чистом Прологе вся информация относительно определенной ветви вычисления при осуществлении возврата теряется. Поэтому в чистом Прологе не существует простого способа нахождения множества всех решений для некоторого вопроса или даже определения того, сколько существует решений для данного вопроса.
В этом разделе обсуждаются предикаты, позволяющие отвечать на вопросы второго порядка, Будем называть такие предикаты множественными.Их можно считать новыми примитивами, однако нельзя трактовать как подлинные расширения Пролога, поскольку они могут быть определены в самом Прологе посредством его внелогических предикатов, особенно таких, как assertи retract.Мы представляем их в языке в виде некоторого расширения более высокого порядка - квантификации по всем решениям - и покажем далее, как они могут быть реализованы. Как и при стандартной реализации отрицания, реализация множественных предикатов лишь аппроксимирует их логическое описание. Однако эта аппроксимация очень полезна во многих применениях, что будет показано в следующем разделе.
Рассмотрим пример применения множественных предикатов, используя представленную на рис. 17.1часть библейской базы данных программы 1.1.
отец(терах,авраам). отец(аран,лот).
отец(терах,нахор). отец(аран, милка).
отеи(терах,аран). отец(аран,иска).
отец(авраам,исаак).
мужчина(авраам).` мужчина(аран). женщина(иска).
мужчина(исаак). мужчина(нахор). женщина(милка).
мужчина(лот).
Рис. 17.1.Часть библейской базы данных.
Пусть требуется отыскать всех детей определенного отца. Естественно представить себе предикат дети(Х.Детки),гдеДетки-список детей X,которые должны быть «извлечены» из фактовотец,представленных на рис. 17.1.Наивный подход, .основанный на применении накопителя,реализуется следующим образом:
дсти(Х,Сs)дети(Х,[ ].Сs). дети(Х,А,Сs)
отец(Х,С). not mcmber(C,A), !,дети(Х,[С | A],Cs).
дети(X,Cs,Cs).
Эта программа на такой вопрос, как дети (mepax.Xs)?,успешно отвечаетXs =[аран.пахор.аараам].Однако подход с использованием накопителей имеет два серьезных недостатка, которые препятствуют развитию более общих множественных предикатов. Первый недостаток состоит в том, что всякий раз, когда некоторое решение добавляется в накопитель, полное дерево поиска обходится заново. В общем случае повторные вычисления должны быть запрещены. Второй недостаток связан с тем, что существуют задачи с общностью. На такой вопрос, какдети (X,Cs)?,будет дан ответХ = терах, Cs = [аран,нахор,авраам],а альтернативное решение при возврате из-за использования отсечения оказывается недоступным. Как только «свободные» переменные конкретизированы, получить альтернативное решение становится невозможно. Удаление же отсечения вызовет некорректное поведение программы при задании вопросадети (терах, Н).
Предпочтительный способ реализации множественных предикатов в Прологе основан на операционном поведении Пролога, в частности вызывающем побочные эффекты программы. Как это сделать, будет показано в конце раздела.
Остановимся на двух примитивных множественных предикатах. Отношение bag_of(Term,Goal,Instances)истинно, если Instances -мультимножество всех примеров терма Term,для которых цель Goalистинна. Кратные тождественные решения сохраняются. Отношение set_of(Term,Goal,Instances)является некоторым усовершенствованием отношения bag-of,где Instancesупорядочено, а повторяющиеся элементы удалены.
Отношение детилегко теперь записать следующим образом:
дети(Х.Детки) set_of(С,отец(Х,С),Детки).
Завершаемость выполнения множественных предикатов зависит от завершения работы с целью, примеры которой собираются. Для этой цели должен быть выполнен обход полного дерева поиска. Следовательно, бесконечная ветвь, встретившаяся в дереве поиска, приведет к незавершаемости поиска.
Множественные предикаты могут иметь кратные решения. Рассмотрим вопрос set_of(Y,omeц(X,Y),Дemки)?.Существует несколько альтернативных решений, соответствующих различным значениям X.Например, {X = терах.Детки = [авраам. нахор,аран]}и [X =авраам, Детки = [исаак]}являются равно законными решениями, которые должны быть получены при поиске с возвратами.
Однако существует другая интерпретация, применимая к вопросу set-off(Y, omeц(X,Y),Дemки)?.Он может рассматриваться как вопрос о всех детях (независимо от отца), упомянутых в фактах программы. В логической интерпретации это означает, чтоДеткиесть множество всех значений У, таких, что существует некоторое X,для которого отношение omец(X,Y)истинно. Для представленных на рис. 17.1фактов существует единственное решение этого вопроса:Детки =[авраам, нахор, аран, исаак, лот, милка люка].Чтобы отличать подобные «экзистенциальные» вопросы от обычных, решаемых поиском с возвратами, используем дополнительное обозначение. Наш вопрос в принятой для вопросов второго типа форме запишется так: set_of(Y,X(отец (X,Y), Детки). Вобщем случае некоторый вопрос VGoal означает, что существует некоторое У, такое, что цель Goalистинна.
Множественные предикаты могут быть вложенными. Например, все отношения отец -дети могут быть вычислены при ответе на вопрос set_of (Отец-Детки, set_of(X,родитель (Отец,Х).Детки),Ys)?. Соответствующим решением будет[терах – [авраам, нахор,аран], авраам – [исаак], аран-[лот, милка,иска]].
Существуют два возможных способа определения поведения предиката set_of(X.GoalJn.flaiKes),когда решение цели Goalзавершается отказом, т.е. когда она не имеет истинных примеров. Определим предикаты set_ofи bag_ofтак, чтобы их вычисление всегда было успешным; для этого, когда цель Goalне имеет решений,Instancesопределяется как пустой список. Такое определение предполагает, что «знаниями» в программе является все то, что истинно. Это аналогично аппроксимации отрицания «отрицанием как безуспешным вычислением».
Можно определить варианты предикатов set_ofи bag_of,вычисление которых будет приводить к отказу, когда решений не существует. Эти новые отношения обозначим как set_ofи bag_of1и дадим их определения в программе 17.1.
Множественные предикаты
set_of1(X,Goal,Instances) Instances-этомножество примеровХ(если такие существуют), для которых цель Goalистина.
set_of1(X,Goal, Instances)
set_of(X, Goal. Instances), Instances = [I | Is].
bug_ofl (X.Goal,Instances) Instances--этомультимножество примеров X(если такие существуют), для которых цель Goalистинна. Кратность элемента мультимножества равна числу различных путей, которыми может быть доказана цельGoalдля этого элемента, используемого в качестве примера X.
bag_of1(X, Goal, Instances)
bag_of(X, Goal, Instances), Instances = [I|Is].
size_of(if(X,Goal.N)- N-число различных примеров X.таких, что цель Goalистинна.
size_of(X,Goal,N) set_of(X,Goal,Instances), length(Instances,N).
length(Xs,N) См. программу 8.11.
Программа 17.1.Множественные предикаты.
Многие из рассмотренных ранее рекурсивных процедур можно переписать с использованием множественных предикатов. Например, программа 7.9для удаления из списка повторяющихся элементов легко определяется с помощью предикатов для проверки принадлежности элементов множеству:
no_doubles(Xs,Ys) set_of(X,member(X, Xs),Ys).
Это определение, однако, значительно менее эффективно, чем непосредственно записанная рекурсивная процедура. Вообще в современных реализациях Пролога рекурсивные программы оказываются более эффективными, чем программы, использующие множественные предикаты.
Другие вспомогательные предикаты второго порядка можно определить, используя рассмотренные основные множественные предикаты. Так, подсчитать число различных решений можно с помощью программы size_of(X, Goal, N), которая определяет число NрешенийХдля некоторой цели Goal,Этот предикат представлен в программе 17.1.Если цель Goalне имеет решений, переменная N принимает значение 0.Если требуется, чтобы выполнение предиката size_ofпри отсутствии решений завершалось отказом, можно вместо предиката set_ofиспользовать предикат set_of1.Если же вместо предиката set_ofприменить предикатbug_of,то рассматриваемый нами предикат будет определять число решений с учетом кратных решений.
Еще один вспомогательный множественный предикат предназначен для проверки того, все ли решения вопроса удовлетворяют определенному условию. Программой 17.2определяется предикат for_all (Goal,Condition),истинный, когда условие
for_all(Goal, Condition)
Для всех решений цели Goalусловие Conditionистинно.
for_all(Goal, Condition)
set_of(Condilion, Goal, Cases),check (Cases).
check ([Case | Cases]) Case, check (Caces).
check([ ])
Программа 17.2.Применение множественных предикатов.
Conditionистинно для всех значений цели Goal.В его определении использована метапеременная Case.
Спомощью вопросаfor_all(отец(Х,С),мужчина(С))?проверяется, какие отцы имеют детей только мужского пола. Ему соответствуют два ответа:Х = терахиХ = авраа.м.
Более простой и эффективный, но менее универсальный вариант предиката for-allможно написать без использования множественных предикатов. Подобный эффект дает совместное использование недетерминизма и отрицания как безуспешного вычисления. Рассмотрим новое определение
for_all(Goal,Conditon) not(Goal, notCondition).
Теперь предикат успешно отвечает на такой вопрос, как for_all(отец(терах, X), мужчина (Х))?,однако попытка дать решение вопросаfor_all(отец(Х, С), .мужчина(С))?приводит к отказу.
В заключение этого раздела покажем, как реализовать простой вариант предиката bag_of.Это обсуждение преследует две цели: оно иллюстрирует определенный стиль реализации множественных предикатов и вводит вспомогательный предикат, который пригодится нам в следующем разделе. Предикат find_all_dl(X, Goal, Instances)истинен, если Instances-мультимножество примеров X,представленных разностным списком, для которых цель Goalистинна. Эта процедура отличается от процедуры bag_ofтем, что поиск альтернативных решений происходит без использования возвратов.
Определение предиката find_all_dlдает программа 17.3.Программа имеет только операционное толкование. В ней имеются два этапа, описанные двумя предложениями find_all_dl.Явный отказ в первом предложении гарантирует выполнение второго предложения. Первый этап находит все решения для цели Goal, используя управляемый отказами цикл, добавляющий по мере обработки соответствующие примеры X.Второе предложение выбирает эти решения.
Введение "Smark"существенно для корректного выполнения вложенных множественных выражений заимствования одним множественным выражением решений, полученных другим множественным выражением.
find_all_dl (X.Goal,Instances ) Instances-этомультимножество примеров X,для которых цель Goalистинна. Кратность элемента мультимножества равна числу различных путей, которыми может быть доказана цель Goalдля этого элемента, используемого в качестве примера X.
find_all_dl(X, Goat, Xs)
asserta(Sinstances($mark)), Goal,
asserta($instance(X)), fail
find_all_dl(X, Goal, Xs\Ys)
n-rrac-*($instance(X)), reap(X,Xs\Ys),!.
reap(X.Xs\Ys)
X Smark, retract(Sinstance(Xl)),!,
reap(Xl.Xs\[X|Ys]). reap(SniLii-k.Xs .Xs).
Программа 17.3.реализация множественного предиката с использованием разностных списков и внелогических предикатов assertи retract.
Упражнения к разд. 17.1
1.Используя множественное выражение, определите предикат intersect( Xs.Ys.Zs)для поиска пересечения Zsдвух списков Xsи Ys.Что должно произойти, если указанные списки не пересекаются? Сравните вашу программу с рекурсивным определением предиката intersect.
17.2. Применения множественных выражении
Множественные выражения являются существенным дополнением к Прологу. Их использование вкупе с другими, уже рассмотренными методами программирования для многих задач приводит к искусным решениям. В этом разделе в качестве примеров представлены три программы: программа обхода графа в ширину, программа трассировки СБИС по алгоритму Ли и программа порождения ключевого слова в контекстном указателе.
В разд. 14.2были рассмотрены три программы 14.8, 14.9и 14.10для обхода графа в глубину. Здесь обсуждаются эквивалентные программы для обхода графа в ширину.
connected (X ,Y)
Связь вершины Л' с вершиной У в ориентированном ациклическом графе определяется предложением edge/2.
connected(X.V) connected_bfs([X | Xs])\Xs,Y).
connected_bfs([ ] \ [ ], Y) !, fail.
connected_bfs([X | Xs]\Ys, X).
connected_bfs([X | Xs] \ Ys, Y) ^-
find_all_dI(N,edge(X,N),Ys\Zs),
connected_bfs(Xs\Zs,Y).
Дачные
edge(a,b). edge(a,c). edge(a,d). edge(a,e).
edge(f,i). edge(c,f). edge(c,g). edge(f.h).
edge(e.k). edge(d.j). edge(x,y). edge(y,z).
edge(z,x). edge(y.u). edge(z,v).
Программа 17.4.Программа и тестовые данные для проверки алгоритма обхода в ширину ориентированного ациклического графа.
Основным отношением является connected(X,Y),которое истинно, если вершины Х иYсвязны. Это отношение определено в программе 17.4.Поиск в ширину реализуется посредством ведения такой очереди вершин, следуя которой происходит обход графа в ширину. Соответственно предложение connectedвызывает отношениеconnected_bfs(Queue,Y),которое истинно, еслиYпринадлежит связному компоненту графа, представленному вершинами в очереди Queue.
При каждом обращении к предикату connectd_bfsтекущая вершина извлекается из очереди, находится множество связанных с ней вершин, которые добавляются в конец очереди. Очередь представлена разностным списком. Кроме того, здесь используется множественный предикатfind_all_dl.Если очередь пуста,товыполнение программы завершается отказом. Поскольку разностные списки являются неполными структурами данных, необходимо предусмотреть явную проверку пустоты очереди. В противном случае выполнение программы может не завершаться,
Рассмотрим факты edgeв программе 17.4,представляющие граф, показанный на рис. 14.3слева. Для них вопрос connected(a.X)дает решенияb, с, d, e, f, g, j, k, h, iкак результат обхода графа в ширину.
Программа 17.4,подобно программе 14.8,пригодна для обхода конечного дерева или ориентированного ациклического графа. В случае циклического графа выполнение программы не завершится.
connected(X. Y)
Связь вершины Х с вершиной У в графе определяется предложением edge/ 2.
connected(X,Y) connected(X | Xs]\Xs, Y,[X]).
connected ([ ]\[ ], Y, Visited) !, fail.
connected ([A | Xs]\Ys, A, Visited).
connected ([A | Xs]\Ys,B, Visited)
set_of(N,edge(A,N),Ns),
filter([Ns, Visited, Visited],Xs\Ys,Xsl),
connected(Xsi, B, Visited1).
filter([N [ Ns], Visited, Visited l,Xs,Xsl)
rnember(N, Visited),
filter(Ns, Visited, Visitedl, Xs, Xs1).
filter([N|Ns],Visited,Xs\[N|Ys],Xs\Ys)
not rnembcr(N,Visited),
filter(Ns,[N | Visited], Visitedl,Xs\Ys,Xsl).
filter([ ],V,V,Xs, Xs).
Программа 17.5 Проверка связности графа путем обхода в ширину.
По сравнению с программой 17.4программа 17.5более совершенна, в ней, в частности, ведется список просмотренных вершин графа. В конец очереди добавляются не все дочерние вершины, а только те, которые еще не просматривались, Такая проверка в программе 17.5выполняется с помощью предиката filter.
На самом деле программа 17.5является более мощной, чем ее эквивалент с обходом в глубину - программа 14.10.Она не только осуществляет корректный обход любого конечного графа, но с тем же успехом может использоваться и для обхода бесконечных графов. Полезно заметить, что расширения чистого Пролога необходимы для увеличения эффективности поиска на графах. Используя чистый Пролог, можно писать корректные программы поиска на конечных деревьях и ориентированных ациклических графах. Добавление отрицания позволяет реализовать корректный поиск на конечных графах с циклами, а множественные выражения необходимы для работы с бесконечными графами. На рис. 17.2эти соображения представлены в сжатом виде.
Определение пути между двумя вершинами графа представляет собой несколько более сложную задачу, чем поиск в глубину. Вместе с каждой вершиной в очереди здесь необходимо хранить список вершин, по которым проходит путь, связывающий ее с исходной вершиной. Этот метод демонстрируется в программе 18.6 вследующей главе.
(1)Конечные деревья и ориентированные ациклические графы. Чистый Пролог.
(2)Конечные графы.
Чистый Пролог +отрицание.
(3)Бесконечные графы.
Чистый Пролог +множественные выражения +отрицание.
Рис. 17.2.Средства Пролога для решения различных задач поиска на графах.
Другой пример объединяет мощность недетерминированного программирования со средствами программирования второго порядка. Это программа определения трассы минимальной стоимости между двумя точками схемы, реализующая алгоритм Ли.
Задача формулируется следующим образом. Дана сетка, на которой могут быть размещены препятствия. Необходимо найти кратчайший путь между двумя заданными точками сетки. Пример сетки с препятствиями показан на рис. 17.3.Жирной сплошной линией показан кратчайший путь между точкамиАиВ.Препятствия представлены заштрихованными прямоугольниками.
Прежде всего сформулируем задачу в подходящем для программирования виде. СБИС моделируется сеткой точек, обычно располагаемой в первом квадранте декартовой плоскости. Трассой называется путь между двумя точками сетки, составленный только из горизонтальных и вертикальных отрезков, располагаемых в пределах сетки и не проходящих через препятствия.
Точки на плоскости представлены своими декартовыми координатами и обозначены как Х - Y.На рис. 17.3точкаАимеет координаты 1 - 1,точкаВ-координаты 5 - 5.Обозначение удобно для восприятия и использует «-»в качестве инфиксного бинарного оператора. Путь, определяемый программой, представляется списком точек, лежащих на пути, включая концевые точки. Так, трасса, показанная на рис. 17.3жирной сплошной линией, есть список [5 —5,5 — 4,5 — 3, 5 - 2,4 - 2,3 - 2,2 - 2,1 - 2,1 -7].
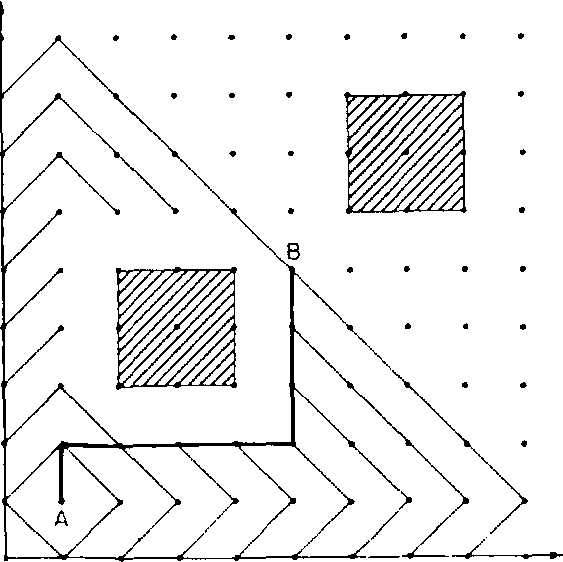
Рис. 17.3.Трассировка СБИС по алгоритму Ли
Предикатом верхнего уровня в программе является предикат lee_route(А.В, Obstacles,Path),где Path-кратчайшая трасса из точкиАв точкуВсхемы.Obstacles -препятствия на сетке. Программа выполняется в два этапа. На первом этапе, начиная с исходной точки, генерируются последовательные волны, состоящие из соседних точек сетки. Процесс продолжается до тех пор, пока не будет достигнута конечная точка. На втором этапе из накопленных волн выделяется искомый путь. Рассмотрим некоторые элементы программы 17,6;представляющей собой полную программу трассировки схемы по алгоритму Ли.
Волны определяются индуктивно. Начальная волна-список [А]. Последова-
lee_route (Source, Destination, Obstacles, Path)
Path-путьминимальной длины, ведущий из исходной точки Source кконечной точке Destinationи не пересекающий препятствий Obstacles.
lee_route(A,В, Obstacles, Path)
waves(B,[[AJ,[ ]J, Obstacles, Waves), path(A,B, Waves, Path).
waves (Destination, WavesSoFar, Obstacles, Wares)
Wares-список волн, включающий «текущие», волны WavesSoFar(возможно, кроме последней), которые ведут к точке Destination,минуя препятствия Obstacles.
waves(B,[Wave | Waves],Obstacles, Waves) member(B,Wave),!.
waves(B, [Wave, LastWave | LastWaves], Obstacles, Waves)
next_wave(Wave, LastWave, Obstacles, NextWave),
waves(B, [NextWave, Wave, LastWave | LastWaves], Obstacles, Waves).
next_wave (Wave. LastWave, Obstacles, NextWave)
NextWave-множество допустимых точек из волны Wave,исключая точки из «последнейволны» LastWaveи волны
Wave,а также точки, покрытые препятствиями Obstacles.
next_wave(Wave, LastWave, Obstacles, NextWave)
set_of(X,admissible(X, Wave, LastWave, Obstacles), NextWave).
admissible(X, Wave, LastWave, Obstacles)
adjacent(X, Waves, Obstacles)
not member(X, LastWave),
not member(X,Wave),
adjacent (X,Wave,Obstacles)
member(Xl,Wave),
neighbor(Xl,X),
not obstucted(X,Obstracles).
neighbor(XI -Y.X2-Y) next_to(Xl,X2).
neighbor(X-Yl,X-Y2) next_to(Yl,Y2).
next_to(X,Xl) Xl:- X+1.
next_to(X,Xl) X>0,X1 :=Х-1.
obstucted(Point, Obstacles)
member(Obstacles,Obstacles),obstructs(Point, Obstacle).
obstructs(X-Y, obstacle(X-Yl,X2-Y2))YlY,YY2.
obstructs (X-Y, obstacle(Xl-Yl,X-Y2))YlY,YY2.
obstructs(X - Y, obstacle (X 1 -Y,X2-Y2))X1X,XX2.
obstructs(X-Y, obstacle(Xl-Yl,X2-Y))XlX,XX2.
path(Source, Destination, Waves. Path)
Path-путьиз точки Sourscв точку Destination,проходящий через волны Waves.
path(A, A, Waves, [A]) !.
path(A, B,[Wave | Waves],[B | Path])
member (В1, Wave),
neighborВ1,В1),
!, path(A, Bl, Waves, Path).
