1. Алгебраическая форма записи комплексного числа. Арифметические операции с комплексными числами в алгебраической форме записи.

Ко́мпле́ксные чи́сла — расширение множества вещественных чисел, обычно обозначается . Любое комплексное число может быть представлено как формальная сумма , где и — вещественные числа, — мнимая единица.

Запись комплексного числа в виде , , называется алгебраической формой комплексного числа.

Сумма и произведение комплексных чисел могут быть вычислены непосредственным суммированием и перемножением таких выражений, как обычно раскрывая скобки и приводя подобные, чтобы представить результат тоже в стандартной форме (при этом надо учесть, что ):

Свойство сложени: Сумма двух комплексных чисел z1=a+bi и z2=c+di будет комплексное число вида z=z1+z2= a+bi + c+di = a+c +(b+d)i 

Свойство вычитания: Разность двух комплексных чисел z1=a+bi и z2=c+di будет комплексное число вида z=z1−z2= a+bi − c+di = a−c +(b−d)i 

Свойство умножения: Произведение двух комплексных чисел z1=a+bi и z2=c+di будет комплексное число вида z=z1 z2= a+bi c+di = ac−bd +(ad+bc)i 

Свойство деления: Частное двух комплексных чисел z1=a+bi и z2=c+di будет комплексное число вида z=z2z1=c+dia+bi=c2+d2ac+bd+c2+d2bc−adi

2. Геометрическая интерпретация комплексного числа на комплексной плоскости.

Рассмотрим плоскость с прямоугольной системой координат. Каждому комплексному числу сопоставим точку плоскости с координатами (а также радиус-вектор, соединяющий начало координат с этой точкой). Такая плоскость называется комплексной. Вещественные числа на ней занимают горизонтальную ось, мнимая единица изображается единицей на вертикальной оси; по этой причине горизонтальная и вертикальная оси называются соответственно вещественной и мнимой осями.

Часто бывает удобно рассматривать на комплексной плоскости также полярную систему координат, в которой координатами точки являются расстояние до начала координат (модуль) и угол радиус-вектора точки (показанного синей стрелкой на рисунке) с горизонтальной осью (аргумент). Подробнее см. ниже.

В этом наглядном представлении сумма комплексных чисел соответствует векторной сумме соответствующих радиус-векторов. При перемножении комплексных чисел их модули перемножаются, а аргументы складываются. Если модуль второго сомножителя равен 1, то умножение на него геометрически означает поворот радиус-вектора первого числа на угол, равный аргументу второго числа. Этот факт объясняет широкое использование комплексного представления в теории колебаний, где вместо терминов «модуль» и «аргумент» используются термины «амплитуда» и «фаза».

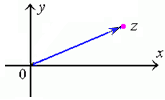
3. Модуль и аргумент комплексного числа.

Модулем (абсолютной величиной) комплексного числа называется длина радиус-вектора соответствующей точки комплексной плоскости (или, что то же, расстояние между точкой комплексной плоскости, соответствующей этому числу, и началом координат).

Модуль комплексного числа обозначается и определяется выражением . Часто обозначается буквами или . Если является вещественным числом, то совпадает с абсолютной величиной этого вещественного числа.

Для любых имеют место следующие свойства модуля. :

1) , причём тогда и только тогда, когда ;;

2) (неравенство треугольника);

3) ;

4) .

Из третьего свойства следует , где . Данное свойство модуля вместе с первыми двумя свойствами вводят на множестве комплексных чисел структуру двумерного нормированного пространства над полем .

5) Для пары комплексных чисел и модуль их разности равен расстоянию между соответствующими точками комплексной плоскости.

Угол (в радианах) радиус-вектора точки, соответствующей числу , называется аргументом числа и обозначается .

• Из этого определения следует, что ; ; .

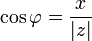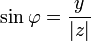• Для комплексного нуля значение аргумента не определено, для ненулевого числа аргумент определяется с точностью до , где  — любое целое число.

• Главным значением аргумента называется такое значение , что 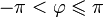. Часто главное значение обозначается ^[4]. Главное значение аргумента обратного числа отличается знаком от аргумента исходного: .
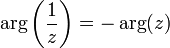