6.1.2. Общая схема кластеризации.

Этапы:

1. Выделение характеристик объектов;

2. Выбор метрики;

3. Выбор метода кластеризации и разбиение объектов на группы;

4. Представление результатов.

Выделение характеристик:

1. Выбор свойств, характеризующих объекты (количественные и качественные характеристики);

2. Нормализация характеристик (приведение к единой шкале);

3. Представление объектов в виде характеристических векторов.

Выбор метрики

Метрика выбирается в зависимости от пространства, где расположены объекты. Если все координаты объекта непрерывны и вещественны, то используется метрика Евклида:

Представление результатов

Обычно используется один из следующих способов представления кластеров:

1. Центроидами;

2. Набором характерных точек;

3. О граничениями кластеров.

6.1.3. Методы кластеризации.

Алгоритм k-средних (k-Means)

1. Выбрать k точек, являющихся начальными «центрами масс» кластеров (любые k из n объектов или вообще k случайных точек);

2. Отнести каждый объект к кластеру с ближайшим «центром масс»;

3. Пересчитать «центры масс» кластеров согласно текущему членству;

4. Если критерий остановки алгоритма не удовлетворен, вернуться к шагу 2.

Критерии остановки:

1. Отсутствие перехода объектов из кластера в кластер на шаге 2;

2. Минимальное изменение среднеквадратической ошибки.

Достоинства: алгоритм быстро работает и прост в реализации.

Недостатки:

• алгоритм создает только кластеры, похожие на гиперсферы;

• алгоритм чувствителен к начальному выбору «центров масс».

Иерархические алгоритмы (иерархическое группирование)

Наибольшее распространение получили агломеративные процедуры, основанные на последовательном объе­динении кластеров (разбиение «снизу-вверх»).

На первом шаге все объекты считаются отдельными кла­стерами. На каждом последующем шаге два ближайших кластера объединяются в один. Каждое объединение уменьшает число кластеров на один так, что в конце концов все объекты объединяются в один кластер. В результате образуется дендрограмма, отображающая результаты группирования объектов на всех шагах алгоритма.

Вид дендрограммы зависит от выбранного способа измерения расстояний между кластерами.

Достоинства: возможность проследить процесс выделения группировок и иллюстрация соподчиненности кластеров.

Н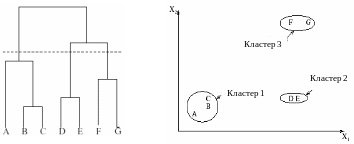 едостаток: квадратичная трудоемкость.

Минимальное покрывающее дерево

Позволяет производить иерархическую кластеризацию «сверху-вниз».

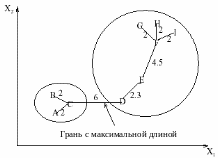
Объекты представляются вершинами связного неориентированного графа с взвешенными ребрами, где вес ребер – это их длина (расстояние между объектами). Нужно удалить ребра как можно большей суммарной длины, оставив граф связным. При этом получается дерево с минимальной суммарной длиной ребер.

Алгоритм Прима:

1. Выбирается произвольная вершина. Она образует начальное дерево.

2. Измеряется расстояние от нее до всех других вершин.

3. До тех пор пока в дерево не добавлены все вершины:

1. Найти ближайшую вершину, с минимальным расстоянием до дерева;

2. Д обавить ее к дереву;

3. Пересчитать расстояния от вершин до дерева: если расстояние до какой-либо вершины из новой вершины меньше текущего расстояния от дерева, то старое расстояние от дерева заменить новым.

4. Разбить объекты на заданное число кластеров в соответствии с максимальными длинами ветвей дерева.

Метод ближайшего соседа

Пока существуют объекты вне кластеров:

1. Для каждого такого объекта выбрать ближайшего соседа, кластер которого определен, и если расстояние до этого соседа меньше порога – отнести его в тот же кластер, иначе можно создать новый кластер;

2. Увеличить порог при необходимости.

Достоинство: простота.

Недостаток: низкая эффективность.

Нечеткая кластеризация

Непересекающаяся (четкая) кластеризация относит объект только к одному кластеру.

Нечеткая кластеризация считает для каждого объекта x_i степень его принадлежности u_ik к каждому из k кластеров.

Схема нечеткой кластеризации:

1. Выбрать начальное нечеткое разбиение N объектов на K кластеров путем выбора матрицы принадлежности U размера N x K (обычно u_ik  [0;1]);

2. Используя матрицу U, найти значение критерия нечеткой ошибки. Например,

Перегруппировать объекты с целью уменьшения ошибки.

3. Повторять шаг 2, пока матрица U меняется.

Достоинства:

1. Отсутствие необходимости в априорных предположениях относительно структуры данных (вид и параметры распределения вероятности по кластерам, центров плотности);

2. Отсутствие ограничений на геометрию кластеров;

3. Время выполнения алгоритма мало зависит от числа компонент входных векторов.

Недостаток: большое время выполнения алгоритма, характеризуемое порядком от числа элементов.