СИСТЕМИ ДИФЕРЕНЦІАЛЬНИХ РІВНЯНЬ

Означення. Система вигляду

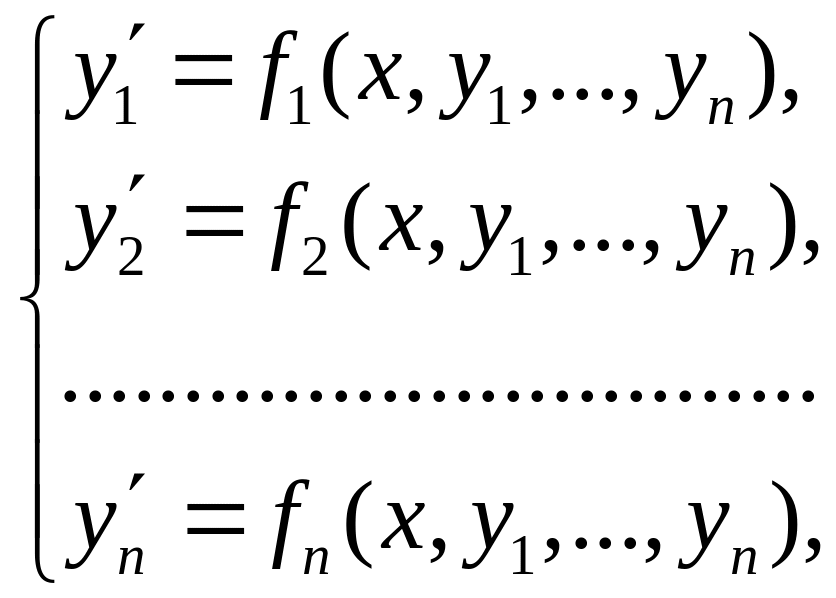(1)

де – незалежна змінна, – невідомі функції змінної , – відомі функції змінних, які визначені на множині , називається нормальною системою диференціальних рівнянь першого порядку. Якщо всі функції не залежать від змінної , то систему

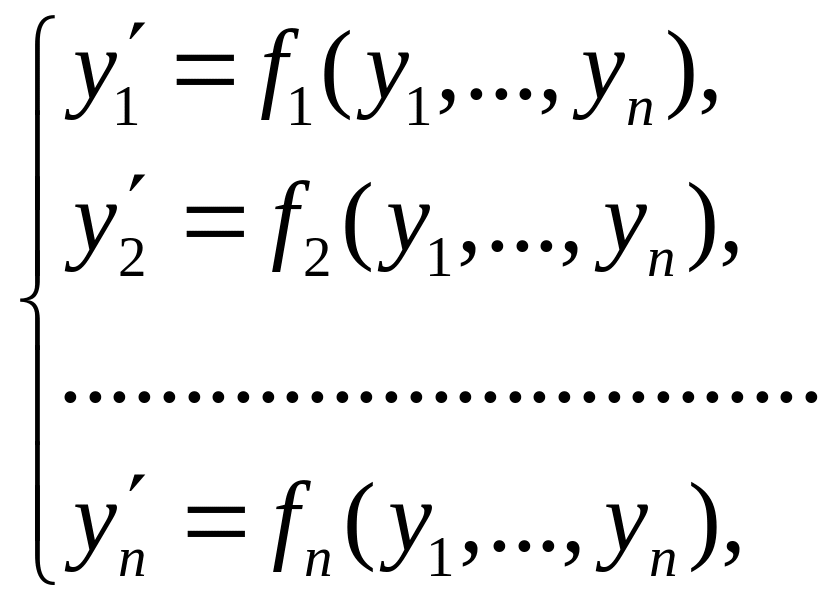
називають автономною або стаціонарною системою диференціальних рівнянь.

Нехай – відомі дійсні числа такі, що Рівності

(2)

називаються початковими умовами нормальної системи (1).

Сукупність функцій

, (3)

які диференційовні на проміжку , називається розв’язком системи (1) на цьому проміжку, якщо вони кожне рівняння системи перетворюють у тотожність

Задачу знаходження розв’язку системи диференціальних рівнянь (1), який задовольняє початкові умови (2), називають задачею Коші.

Множина

,

де – деякі додатні числа називається замкненим прямокутним паралелепіпедом простору . За теоремою про необхідну і достатню умови компактності множини в просторі паралелепіпед є компактом.

Нехай функції – неперервні на компакті . За теоремою про обмеженість неперервних функцій на компакті існують додатні числа такі, що

для всіх , .

Функції на множині задовольняють умови Ліпшиця за змінними , якщо існують такі додатні числа , що

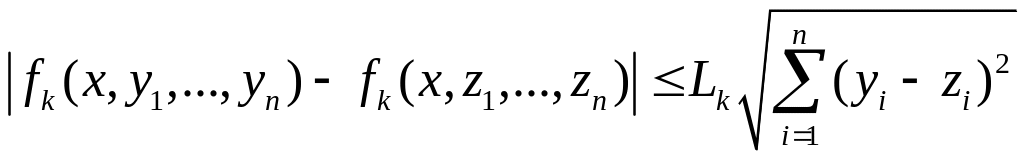
для всіх , і .

Теорема. Якщо функції , , неперервні на замкненому прямокутному паралелепіпеді і задовольняють умови Ліпшиця за змінними , то задача Коші (1)-(2) на відрізку , де 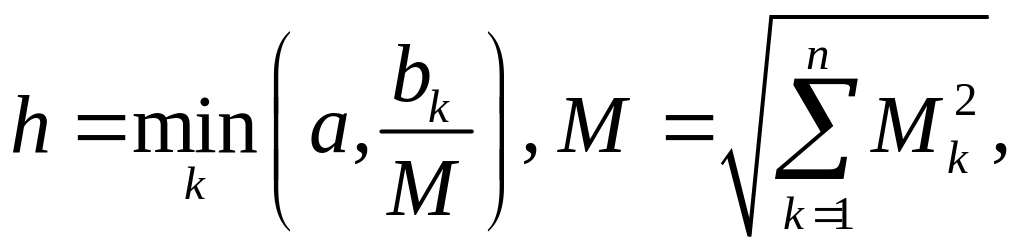має єдиний розв’язок.

1. Зведення лінійного диференціального рівняння -го порядку до нормальної системи диференціальних рівнянь

Нехай є диференціальне рівняння

, (1.1)

де – відомі функції, визначені на множині .

Позначимо

. (1.2)

Оскільки – невідома функція, то – також невідомі функції. При цьому

,

.

Увівши нові невідомі функції (1.2), лінійне диференціальне рівняння -го порядку (1.1) можна замінити наступною нормальною системою диференціальних рівнянь

(1.3)

Нормальну систему диференціальних рівнянь (1) можна звести до диференціального рівняння -го порядку. Але це можна зробити лише за певних умов і робиться воно значно складніше.

2. Система лінійних однорідних диференціальних рівнянь

першого порядку

Означення. Система вигляду

(2.1)

де – відомі неперервні на проміжку функції, – шукані диференційовні функції, називається системою лінійних однорідних диференціальних рівнянь першого порядку –ЛОС.

Якщо з коефіцієнтів системи побудувати матрицю , а з функцій – вектор-функцію :

то системи (2.1) запишеться у вигляді:

. (2.2)

Такий запис системи (2.1) називається векторно-матричною формою.

Теорія ЛОС певною мірою нагадує теорію ЛОР. Наведемо без доведення деякі твердження з теорії ЛОС.

Теорема 2.1. Якщо вектор-функція є розв’язком ЛОС (2), то , де – довільна стала, також розв’язок (2.2).

Теорема 2.2. Якщо вектор-функції і є розв’язками ЛОС (2.2), то їх сума також розв’язок (2.2).

Для вектор-функцій мають місце поняття лінійної залежності та лінійної незалежності.

Означення. Система вектор-функцій називається лінійно незалежною на множині , якщо рівність

виконується для всіх тільки за умови, що всі числа дорівнюють нулю: .

Означення. Система вектор-функцій називається лінійно залежною на множині , якщо існують числа такі, що

,

при яких рівність

виконується для всіх .

Означення. Будь-який набір з лінійно незалежних розв’язків ЛОС (2) називається фундаментальною системою розв’язків цієї системи.

Якщо

,

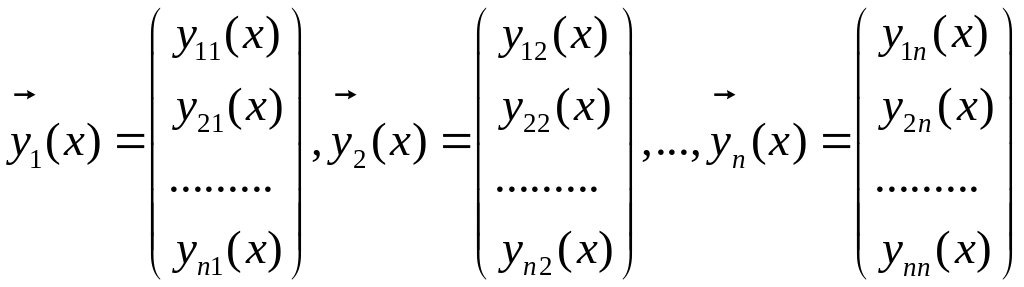то матриця

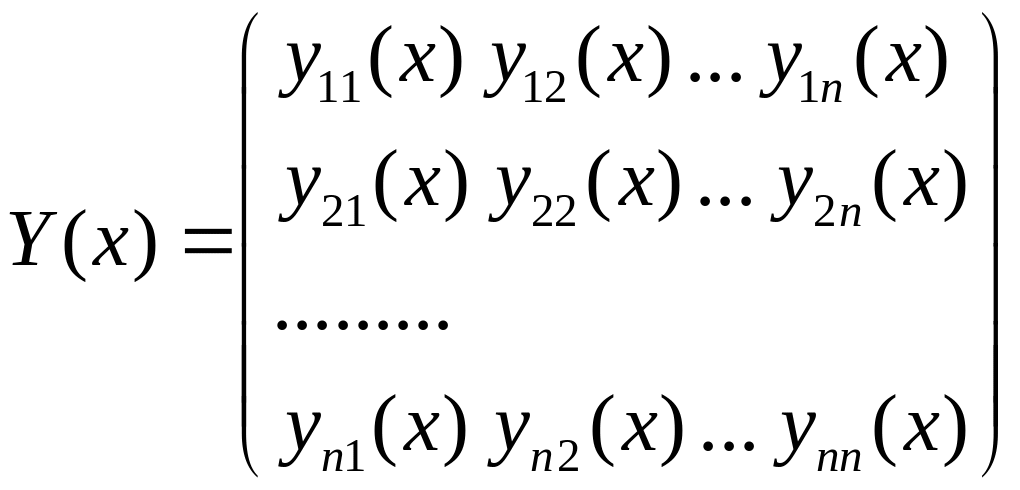(2.3)

називається фундаментальною матрицею розв’язків ЛОС.

Квадратну матрицю при потребі будемо записувати як однорядкову матрицю , елементами якої є вектор-функції .

Матриця (2.3) буде фундаментальною на проміжку тоді і тільки тоді, коли її визначник не дорівнює нулю на цьому проміжку. Визначник фундаментальної матриці розв’язків називається визначником Вронського і позначається :

.

Для визначника Вронського має місце формула Якобі

(2.4)

де , – слід матриці . З формули Якобі випливає, що визначник Вронського не дорівнює нулю на проміжку , якщо він відмінний від нуля хоч би в одній внутрішній точці цього проміжку.

Диференційовна вектор-функція , де – довільні сталі, називається загальним розв’язком ЛОС (2) на проміжку , якщо:

1) на цьому проміжку вона разом зі своїми похідними перетворює рівняння системи в тотожності,

2) для будь-яких і існують сталі такі, що розв’язок задовольняє початкову умову

де .

Теорема 2.3. Якщо – фундаментальна матриця розв’язків ЛОС, то вектор-функція , де – довільний сталий вектор, є загальним розв’язком цієї системи.

Д о в е д е н н я. Нехай вектор-функції на проміжку утворюють фундаментальну систему розв’язків системи.

Утворимо фундаментальну матрицю розв’язків

і знайдемо її похідну (похідною матриці називається матриця, елементами якої є похідні її елементів):

.

Доведемо, що матриця перетворює ЛОС в матричну тотожність на проміжку .

Вектор-функції є розв’язками ЛОС. Тому вони перетворюють її на проміжку у векторні тотожності

.

Виконуючи множення матриці на матрицю нескладно переконатися, що

.

Тому

для всіх .

Доведемо, що – розв’язок ЛОС. Для цього розглянемо різницю :

.

Ми дістали векторну тотожність, яка означає, що – розв’язок ЛОС при будь-якому сталому векторі .

Визначимо вектор так, щоб вектор-функція задовольняла початкову умову для будь-якого і для будь-якого -вимірного сталого вектора :

.

Отже, вектор-функція , де матриця – обернена до матриці , є розв’язком ЛОС і задовольняє початкову умову .

Теорему доведено.