22. Вероятность попадания значений непрерывной случайной величины в заданный интервал для нормального распределения плотности вероятностей.

Для нормально распределенной случайной величины соответственно получим: где   – функция Лапласа. Вывод: вероятность того, что нормально распределенная случайная величина х примет значение, принадлежащее интервалу (a,b), равна: , где a – математическое ожидание,   – среднее квадратическое отклонение данной случайной величины.

23. Расчет вероятности заданного отклонения нормальной случайной величины. Правило трех сигм.

Вычислим вероятность того, что отклонение нормально распределенной случайной величины х от своего математического ожидания по абсолютной величине не превысит  , то есть вероятность осуществления неравенства  . Заменим неравенство с модулем равносильным ему двойным неравенством: Теперь мы можем воспользоваться формулой для нахождения вероятности попадания в заданный интервал нормальной случайной величины, где границами интервала являются Вывод: вероятность того, что отклонение нормально распределенной случайной величины х от своего математического ожидания по абсолютной величине не превысит  , равна:

Правило трех сигм

если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения. . Другими словами, вероятность того, что абсолютная величина отклонения превысит  , составляет всего 0,0027. Такое событие, исходя их принципа невозможности маловероятных событий, можно считать практически невозможным.

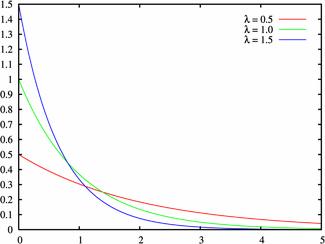
24. Показательное распределение плотности вероятностей непрерывной случайной величины и вероятность попадания в заданный интервал для данного распределения.

Экспоненциальное( показательное) распределение — абсолютно непрерывное распределение, моделирующее время между двумя последовательными свершениями одного и того же события;распред-е плотности вероятности вида вер-ть попадания в заданный интервал: P(a<x<b)=F(b)-F(a)=1-e –лямбда b – 1+e –люмбда а= e –люмбда а-e –лямбда b.

25. Числовые характеристики показательного распределения: математическое ожидание, дисперсия, среднее квадратичное отклонение.

Функция надежности.Пок.распределение: M(x)=1/лямбда,D(x)=1/лямбда в квадрате, σ(Х)=корень D(x)=1/лямбда.Функция отказа-F(t).вер-ть отказа за время t,меньшее время безотказ.работы:P(T<t)=1-e –лямбдаt.T-длительность безотказной работы.Функция надежности-R(t)=1- F(t)=1-(1- e –лямбдаt)=1-1+ e –лямбдаt= e –лямбдаt_.

26. Понятия генеральной совокупности, выборки и степени ее свободы, связных и несвязных выборок, нулевой и альтернативной гипотез.

Генеральная совокупность – совокупность всех объектов (единиц), относительно которых учёный намерен делать выводы при изучении конкретной проблемы.

Выборка (выборочная совокупность)– множество случаев (испытуемых, объектов, событий, образцов), с помощью определённой процедуры выбранных из генеральнойсовокупности для участия в исследовании.

Степень свободы – число независимых (свободных) величин в данной выборке. Характеризуется ср значением и числом элементов. Следовательно любой элемент выборки может быть равен : количество элементов*среднее значение – сумму значений элементов Число степеней свободы у какого-либо параметра определяют как число опытов, по которым рассчитан данный параметр, минус количество одинаковых значений, найденных по этим опытам независимо друг от друга.