Раздел 4 Анализ состояния технологического процесса обработки деталей: а) отверстие в червячном колесе (d3) б) вал под червячное колесо (d3)

Cхема расположения полей допусков для посадки Ø68Н7/k6 представлена на рис. 9.

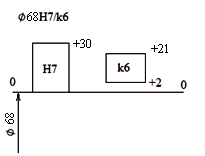
Рис. 10. Посадка червячного колеса на вал.

Рассчитаем параметры посадки:

S(N)_max = D_max - d_min = ESD - eid = 30 -2 = 28 мкм равно наибольшему зазору S_max = 28 мкм;

S(N)_min = D_min - d_max = EID - esd = 0 - 21 = -21 равно наибольшему натягу N_max = 21 мкм;

Cреднее значение параметра посадки равно: S(N)_m = 0,5(S(N)_max + S(N)_min) = 0,5(28 + (-21)) = +3,5 мкм;

Допуск посадки равен TS(N) = S(N)_max – S(N)_min = 28 - (-21) = 49 мкм или TS(N) = Td + TD = 30 + 19 = 49 мкм.

S(N)_m = +3,5 является центром группирования распределения параметра посадки S(N) (зазоров - натягов).

Координата середины поля допуска вала ec = 0,5(es + ei) =0,5(2+21)=11,5 мкм.

Координата середины поля допуска отверстия Ec = 0,5(ES + EI) = 0,5(30 + 0) = +15 мкм.

Средний размер вала – 68+0,0115=68,0115 мм, отверстия - 68 + 0,015 = 68,015 мм. Средние размеры являются центрами группирования погрешностей при изготовлении деталей, на него настраивают станок при обработке.

Предполагаемый диапазон рассеяния (размах) размеров деталей получаемых при обработке:

d₃ = D₃ = A = 68 мм - номинальный размер соединения (задан в условии).

Для отверстия:

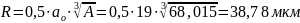
а_о = 19 - коэффициент точности отверстия (из условия).

Для вала:

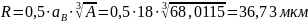
а_В = 18 - коэффициент точности вала.

а) Статистическая обработка результатов многократных равноточных измерений отверстия.

Смоделируем результаты измерения отверстия с помощью Формирователя.

Число измерений N=200 (согласно заданию).

Результаты наблюдений:

67,993	67,998	68,010	68,017	68,031
67,964	67,998	68,010	68,017	68,031
67,970	67,999	68,010	68,017	68,032
67,975	68,000	68,010	68,017	68,032
67,978	68,000	68,010	68,018	68,032
67,978	68,000	68,011	68,018	68,033
67,980	68,000	68,011	68,018	68,033
67,982	68,001	68,011	68,019	68,033
67,982	68,001	68,011	68,019	68,034
67,982	68,001	68,011	68,019	68,034
67,983	68,001	68,011	68,019	68,035
67,983	68,001	68,011	68,019	68,035
67,984	68,001	68,012	68,019	68,036
67,985	68,001	68,012	68,020	68,036
67,986	68,001	68,012	68,021	68,036
67,987	68,001	68,012	68,021	68,036
67,987	68,002	68,012	68,021	68,037
67,989	68,002	68,012	68,022	68,037
67,989	68,003	68,012	68,023	68,037
67,990	68,003	68,012	68,023	68,037
67,990	68,003	68,013	68,023	68,038
67,990	68,004	68,013	68,023	68,039
67,992	68,004	68,013	68,023	68,039
67,992	68,005	68,014	68,024	68,040
67,992	68,005	68,014	68,026	68,042
67,992	68,005	68,014	68,026	68,042
67,993	68,006	68,014	68,027	68,042
67,993	68,006	68,015	68,027	68,042
67,993	68,006	68,015	68,027	68,043
67,994	68,007	68,015	68,028	68,044
67,994	68,007	68,016	68,028	68,046
67,995	68,007	68,016	68,029	68,049
67,995	68,007	68,016	68,029	68,049
67,995	68,007	68,016	68,029	68,053
67,996	68,008	68,017	68,029	68,053
67,996	68,008	68,017	68,029	68,054
67,996	68,008	68,017	68,029	68,057
67,997	68,009	68,017	68,029	68,066
67,997	68,009	68,017	68,030	68,069
67,998	68,009	68,017	68,030	68,070

Минимальное значение наблюдаемого размера равно 67.964 мм, а максимальное равно 68.069 мм, тогда размах R, равный разности полученных предельных значений, равен: R = dmax - dmin = 68,069 - 67,964 = 0,105 мм.

Далее вариационный ряд разбиваем на k=9 интервалов. Величина интервала равна R/k = 0,105/9 = 0,0117 мм, а половина интервала равна 0,5R/k = 0,00585 мм. Находим значения середин интервалов и образуем интервальный ряд, для чего к dmin прибавим значение 0,5R/k, к полученному значению прибавим снова 0,05R/k и так далее, получим в итоге dmax - 0,5R/k, т.е. 68,063 мм.

Далее находим количество наблюдений попавших в каждый из интервалов.

В условиях производства из-за ограниченности числа измерений при обработке вместо математического ожидания и дисперсии получают их приближенные статистические оценки - соответственно эмпирическое среднее и эмпирическую дисперсию s², характеризующие средний результат измерений и степень рассеяния результатов

• =Σx_i(n_i/N)=(67,969*2+67,982*12+67,994*27+68,005*40+68,016*54+ +68,028*32+68,039*21+68,052*6+68,063*3)/200=68,014мм

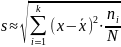= [(-0,045)²*0,01 + (-0,032)²*0,065+ …+

+(-0,02)²*0,14]^0,5≈0,018 мм

Анализируя результаты наблюдений, получаем:

Интервалы действительных размеров di , мм		Среднее значение хi интервала, мм	Число ni деталей в интервале	Отклонение от среднего значения vi=xi-	Частность ni/N
от	до
67,964	67,976	67,969	2	-0,045	0,01
67,976	67,988	67,982	13	-0,032	0,065
67,988	67,999	67,994	28	-0,02	0,14
67,999	68,01	68,005	40	-0,009	0,2
68,01	68,022	68,016	54	0,002	0,27
68,022	68,034	68,028	32	0,014	0,16
68,034	68,046	68,039	22	0,025	0,11
68,046	68,058	68,052	6	0,038	0,03
68,058	68,069	68,063	3	0,049	0,015
=68,014		-	N=200	Σvi= 0,022	Σni/N=1

Центр группирования МХ= 68.014

Максимальное отклонение от среднего |V| = 0.019

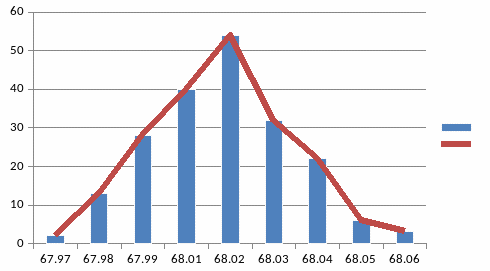
Рис. 11. Гистограмма и полигон распределения.

Анализируя результаты наблюдений, приходим к выводу, что среди них встречаются значения существенно отличающееся от большинства результатов, они являются промахами или грубыми ошибками. Такие наблюдения, могут быть вызваны невнимательностью контролера, попаданием в выборку посторонних деталей, а также другими причинами, нарушающими нормальные условия получения опытных данных.

Зона рассеивания размеров отверстия определяется по результатам виртуальных измерений (ФОРМИРОВАТЕЛЬ) и равна ±V.

Таким образом в данном конкретном случае зона рассеяния равна:

-V − +V

67,995 − 68,033

После исключения грубых ошибок и результатов, не вошедших в зону рассеяния, получим:

Рис. 12. Гистограмма и полигон распределения.

б) Статистическая обработка результатов многократных равноточных измерений вала.

Смоделируем результаты измерения отверстия с помощью Формирователя.

Число измерений N=200 (согласно заданию).

Результаты наблюдений:

67,969	67,997	68,008	68,015	68,026
67,969	67,997	68,008	68,016	68,027
67,973	67,997	68,008	68,017	68,028
67,975	67,997	68,009	68,017	68,029
67,978	67,997	68,009	68,017	68,029
67,979	67,997	68,009	68,018	68,030
67,980	67,998	68,009	68,018	68,030
67,980	67,998	68,009	68,018	68,030
67,981	67,998	68,009	68,020	68,031
67,981	67,999	68,009	68,020	68,031
67,981	67,999	68,009	68,020	68,031
67,982	67,999	68,009	68,021	68,031
67,983	67,999	68,009	68,021	68,033
67,984	67,999	68,009	68,021	68,033
67,984	68,000	68,010	68,021	68,033
67,984	68,001	68,010	68,021	68,033
67,985	68,001	68,010	68,021	68,033
67,986	68,001	68,010	68,021	68,034
67,986	68,002	68,011	68,022	68,034
67,987	68,002	68,011	68,022	68,034
67,987	68,002	68,011	68,022	68,035
67,987	68,002	68,011	68,022	68,035
67,988	68,003	68,012	68,022	68,036
67,988	68,003	68,012	68,022	68,036
67,988	68,003	68,012	68,023	68,036
67,989	68,003	68,012	68,023	68,037
67,989	68,003	68,013	68,023	68,038
67,989	68,003	68,013	68,023	68,039
67,990	68,003	68,013	68,023	68,039
67,990	68,003	68,014	68,024	68,040
67,991	68,004	68,014	68,024	68,040
67,991	68,005	68,014	68,024	68,041
67,991	68,006	68,014	68,024	68,042
67,993	68,006	68,014	68,025	68,043
67,993	68,007	68,014	68,025	68,044
67,995	68,007	68,014	68,026	68,045
67,995	68,007	68,014	68,026	68,046
67,995	68,007	68,014	68,026	68,048
67,996	68,008	68,015	68,026	68,048
67,996	68,008	68,015	68,026	68,053

Минимальное значение наблюдаемого размера равно 67,969 мм, а максимальное равно 68,053 мм, тогда размах R, равный разности полученных предельных значений, равен: R = dmax - dmin = 68,053 – 67,969 = 0,084 мм.

Далее вариационный ряд разбиваем на k=9 интервалов. Величина интервала равна R/k = 0,084/9 = 0,0093 мм, а половина интервала равна 0,5R/k = 0,00465 мм. Находим значения середин интервалов и образуем интервальный ряд, для чего к dmin прибавим значение 0,5R/k, к полученному значению прибавим снова 0,05R/k и так далее, получим в итоге dmax - 0,5R/k, т.е. 68,04835 мм.

Далее находим количество наблюдений попавших в каждый из интервалов.

• = Σx_i (n_i / N)= (67,974*4+67,983*15+67,992*21+ 68,002*32+ 68,011*46+ +68,019*35 +68,029*24 + 68,038*16+68,048*7)/200 =68,012 мм

= [(39,960 - 39,999)²*3/200 + (39,970 - 39,999)²*15/200 + …+ (40,041-39,999)²*3/200]^0,5≈0,016 мм

Анализируя результаты наблюдений, получаем:

Интервалы действительных размеров di , мм		Среднее значение хi интервала, мм	Число ni деталей в интервале	Отклонение от среднего значения vi=xi-	Частность ni/N
от	до
67,969	67,978	67,974	4	-0,038	0,02
67,978	67,987	67,983	15	-0,029	0,075
67,987	67,997	67,992	21	-0,02	0,105
67,997	68,006	68,002	32	-0,01	0,16
68,006	68,015	68,011	46	-0,001	0,23
68,015	68,025	68,019	35	0,007	0,175
68,025	68,034	68,029	24	0,017	0,12
68,034	68,043	68,038	16	0,026	0,08
68,043	68,053	68,048	7	0,036	0,035
=68,012		-	N=200	Σvi= -0,012	Σni/N=1

Центр группирования МХ= 68,011

Максимальное отклонение от среднего |V| = 0,0178

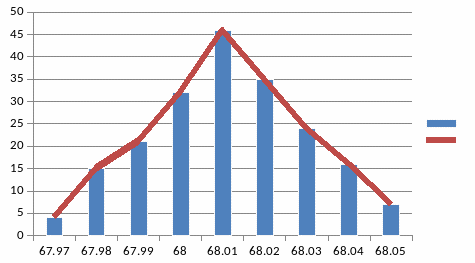
Рис. 13. Гистограмма и полигон распределения.

Анализируя результаты наблюдений, приходим к выводу, что среди них встречаются значения существенно отличающееся от большинства результатов, они являются промахами или грубыми ошибками. Такие наблюдения, могут быть вызваны невнимательностью контролера, попаданием в выборку посторонних деталей, а также другими причинами, нарушающими нормальные условия получения опытных данных.

Зона рассеивания размеров отверстия определяется по результатам виртуальных измерений (ФОРМИРОВАТЕЛЬ) и равна ±V.

Таким образом в данном конкретном случае зона рассеяния равна:

-V − +V

67,993 − 68,029

После исключения грубых ошибок и результатов, не вошедших в зону рассеяния, получим:

Рис. 14. Гистограмма и полигон распределения.