
- •1.1. Объем куба равен 8. Найдите площадь его поверхности.
- •2.9. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
- •2.21. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
- •4.1. Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на .
- •4.5. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота — 10.
- •6.4. Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 14.
- •8.3. В основании прямой призмы лежит прямоугольный треугольник с катетами 9 и 6. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы.
- •9.2. Прямоугольный параллелепипед описан около сферы радиуса . Найдите его объем.
- •11.2. Площадь большого круга шара равна 3. Найдите площадь поверхности шара.
- •13.3. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите .
- •14.4. Найдите объем V части конуса, изображенной на рисунке. В ответе укажите .
2.21. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
 Ответ:
58
2.22. Найдите объем многогранника,
изображенного на рисунке (все двугранные
углы прямые).
Ответ:
58
2.22. Найдите объем многогранника,
изображенного на рисунке (все двугранные
углы прямые).
 Ответ:
90
2.23. Найдите объем многогранника,
изображенного на рисунке (все двугранные
углы прямые).
Ответ:
90
2.23. Найдите объем многогранника,
изображенного на рисунке (все двугранные
углы прямые).
 Ответ:
10
2.24.
Найдите объем многогранника, изображенного
на рисунке (все двугранные углы прямые).
Ответ:
10
2.24.
Найдите объем многогранника, изображенного
на рисунке (все двугранные углы прямые).
 Ответ:40
2.25.
Найдите объем многогранника, изображенного
на рисунке (все двугранные углы прямые).
Ответ:40
2.25.
Найдите объем многогранника, изображенного
на рисунке (все двугранные углы прямые).
 Ответ:
18
3.1.
Длина окружности основания конуса равна
3, образующая равна 2. Найдите площадь
боковой поверхности конуса.
Ответ:
18
3.1.
Длина окружности основания конуса равна
3, образующая равна 2. Найдите площадь
боковой поверхности конуса.
 Ответ:
3
3.2. Объем конуса равен 16. Через
середину высоты параллельно основанию
конуса проведено сечение, которое
является основанием меньшего конуса с
той же вершиной. Найдите объем меньшего
конуса.
Ответ:
3
3.2. Объем конуса равен 16. Через
середину высоты параллельно основанию
конуса проведено сечение, которое
является основанием меньшего конуса с
той же вершиной. Найдите объем меньшего
конуса.
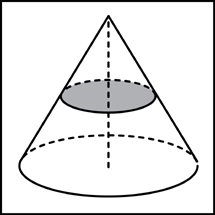 Ответ:
2
3.3. Объем конуса равен 64. Через
середину высоты параллельно основанию
конуса проведено сечение, которое
является основанием меньшего конуса с
той же вершиной. Найдите объем меньшего
конуса.
Ответ:
2
3.3. Объем конуса равен 64. Через
середину высоты параллельно основанию
конуса проведено сечение, которое
является основанием меньшего конуса с
той же вершиной. Найдите объем меньшего
конуса.
Ответ: 8 3.4. Объем конуса равен 120. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Ответ: 15 3.5. Объем конуса равен 128. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Ответ: 16
4.1. Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на .
 Ответ:
12
4.2.
Стороны основания правильной
четырехугольной пирамиды равны 10,
боковые ребра равны 13. Найдите площадь
поверхности этой пирамиды.
Ответ:
12
4.2.
Стороны основания правильной
четырехугольной пирамиды равны 10,
боковые ребра равны 13. Найдите площадь
поверхности этой пирамиды.
 Ответ:
340
4.3.
Стороны основания правильной шестиугольной
пирамиды равны 10, боковые ребра равны
13. Найдите площадь боковой поверхности
этой пирамиды.
Ответ:
340
4.3.
Стороны основания правильной шестиугольной
пирамиды равны 10, боковые ребра равны
13. Найдите площадь боковой поверхности
этой пирамиды.
 Ответ:
360
4.4.
В правильной четырехугольной пирамиде
высота равна 12, объем равен 200. Найдите
боковое ребро этой пирамиды.
Ответ:
360
4.4.
В правильной четырехугольной пирамиде
высота равна 12, объем равен 200. Найдите
боковое ребро этой пирамиды.
 Ответ:
13
Ответ:
13
4.5. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота — 10.
 Ответ:300 5.1.
Прямоугольный параллелепипед описан
около цилиндра, радиус основания и
высота которого равны 6. Найдите объем
параллелепипеда.
Ответ:300 5.1.
Прямоугольный параллелепипед описан
около цилиндра, радиус основания и
высота которого равны 6. Найдите объем
параллелепипеда.
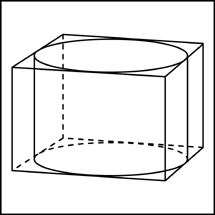 Ответ:
864
5.2. Прямоугольный параллелепипед
описан около цилиндра, радиус основания
и высота которого равны 9,5. Найдите объем
параллелепипеда.
Ответ:
864
5.2. Прямоугольный параллелепипед
описан около цилиндра, радиус основания
и высота которого равны 9,5. Найдите объем
параллелепипеда.
Ответ: 3429,5 5.3. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1,5. Найдите объем параллелепипеда.
Ответ: 13,5
5.4. Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 6. Объем параллелепипеда равен 36. Найдите высоту цилиндра.
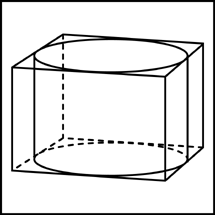 Ответ:
0,25
5.5.
Прямоугольный параллелепипед описан
около цилиндра, радиус основания которого
равен 9. Объем параллелепипеда равен
81. Найдите высоту цилиндра.
Ответ:
0,25
5.5.
Прямоугольный параллелепипед описан
около цилиндра, радиус основания которого
равен 9. Объем параллелепипеда равен
81. Найдите высоту цилиндра.
Ответ: 0,25
5.6. Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 3. Объем параллелепипеда равен 27. Найдите высоту цилиндра.
Ответ: 0,75 5.7. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 8,5. Найдите объем параллелепипеда.
Ответ: 2456,5 6.1. Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 16.
 Ответ:
48
6.2.
Цилиндр и конус имеют общее основание
и общую высоту. Вычислите объем цилиндра,
если объем конуса равен 11.
Ответ:
48
6.2.
Цилиндр и конус имеют общее основание
и общую высоту. Вычислите объем цилиндра,
если объем конуса равен 11.
Ответ: 33 6.3. Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 87.
Ответ: 261
