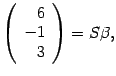- •Линейные пространства
- •§ 1. Понятие линейного пространства
- •§2. Линейная зависимость и линейная независимость векторов линейного пространства
- •§3. Ранг и базис системы векторов
- •Базис и размерность пространства
- •Координаты векторов
- •Координаты векторов
- •Изменение координат вектора при изменении базиса
Координаты векторов
Определение 18.4 Пусть -- -мерное линейное пространство, вещественное или комплексное, -- базис. Тогда произвольный вектор из представим в виде линейной комбинации векторов базиса:
![]()
Числа
![]() называются
координатами вектора
в
базисе
.
Столбец
называются
координатами вектора
в
базисе
.
Столбец
 из
координат вектора называется координатным
столбцом вектора
.
из
координат вектора называется координатным
столбцом вектора
.
Предложение 18.3 Координаты вектора в заданном базисе определяются однозначно.
Доказательство. Предположим противное. Пусть -- базис, в котором у вектора есть два различных набора координат:
![]()
Тогда
![]()
то есть
![]()
Так как наборы координат различны, то хотя бы один из коэффициентов справа отличен от нуля. Следовательно, векторы -- линейно зависимы, что противоречит определению базиса. Полученное противоречие означает, что предположение о наличии двух различных наборов координат неверно.
Предложение 18.4 Пусть в -мерном пространстве задан базис . Тогда координатный столбец суммы векторов равен сумме координатных столбцов слагаемых, координатный столбец произведения вектора на число равен координатному столбцу вектора, умноженному на это число.
Доказательство.
Пусть векторы
и
имеют
координатные столбцы
и
 соответственно.
Отсюда следует, что
соответственно.
Отсюда следует, что
![]()
Поэтому
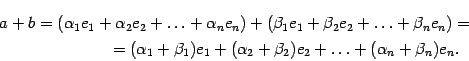
Это равенство означает, что координатный
столбец вектора
![]() имеет
вид
имеет
вид
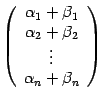 .
Первая часть предложения доказана.
Доказательство второй части предоставляем
читателю.
.
Первая часть предложения доказана.
Доказательство второй части предоставляем
читателю.
Из последнего предложения следует, что как только в -мерном пространстве зафиксирован базис, каждый вектор можно заменить его координатным столбцом, и операциям сложения и умножения на число соответствуют такие же операции над их координатными столбцами. Таким образом, каждое -мерное пространство является, с точки зрения алгебры, копией пространства в вещественном случае, а в комплексном -- копией .
Изменение координат вектора при изменении базиса
Пусть в
-мерном
линейном пространстве
выбран
базис
,
который мы будем для удобства называть
"старый" и другой базис
![]() ,
который мы будем называть "новый".
Возьмем призвольный вектор
из
.
Его координатный столбец в старом базисе
обозначим
,
а в новом --
,
который мы будем называть "новый".
Возьмем призвольный вектор
из
.
Его координатный столбец в старом базисе
обозначим
,
а в новом --
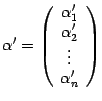 .
Нам нужно выяснить, как связаны друг с
другом координаты в старом и в новом
базисе. Для этого нам сначала нужно
"связать" друг с другом старый и
новый базисы. Запишем разложения новых
базисных векторов по старому базису
.
Нам нужно выяснить, как связаны друг с
другом координаты в старом и в новом
базисе. Для этого нам сначала нужно
"связать" друг с другом старый и
новый базисы. Запишем разложения новых
базисных векторов по старому базису
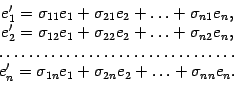
Составим матрицу, столбцами которой служат координатные столбцы векторов нового базиса

Эта матрица называется матрицей перехода от старого базиса к новому.
Замечание
18.1 Матрица перехода
всегда невырождена, то есть
![]() .
.
Предложение 18.5 Координатные столбцы в старом базисе и в новом базисе связаны формулой
|
(18.1) |
где справа стоит произведение матрицы
перехода
![]() на
матрицу-столбец.
на
матрицу-столбец.
Доказательство.
Так как
![]() --
координатный столбец вектора
в
новом базисе, то
--
координатный столбец вектора
в
новом базисе, то

Заменив векторы
![]() их
разложениями по старому базису, получим
их
разложениями по старому базису, получим
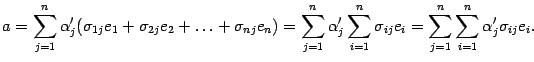
В силу предложения 14.3 изменим порядок суммирования
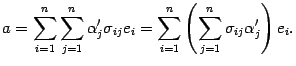
Здесь мы получили разложение вектора
по
старому базису, причем координата
вектора с номером
![]() равна
равна
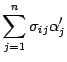 .
Элемент с номером
столбца
.
Элемент с номером
столбца
![]() будет
иметь такой же вид. Следовательно,
формула (18.1)
доказана.
будет
иметь такой же вид. Следовательно,
формула (18.1)
доказана.
Пример 18.4
Пусть
![]() ,
то есть
--
трехмерное векторное пространство.
Пусть задан ортонормированный базис
i, j, k. Выберем другой (новый)
базис
,
то есть
--
трехмерное векторное пространство.
Пусть задан ортонормированный базис
i, j, k. Выберем другой (новый)
базис
![]()
Возьмем вектор
![]() .
Найдем его координаты в новом базисе.
.
Найдем его координаты в новом базисе.
Выпишем матрицу перехода, ее столбцы -- это координаты новых базисных векторов
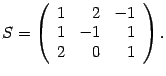
Пусть
--
координатный столбец вектора
![]() в
новом базисе. Тогда
в
новом базисе. Тогда
|
(18.2) |
откуда
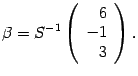
Найдем матрицу
![]() по
формуле (14.14).
Находим определитель
по
формуле (14.14).
Находим определитель
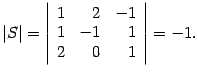
Находим алгебраические дополнения
![]()
Следовательно,
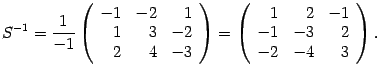
Находим координаты вектора

Таким образом, новые координаты вектора
:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Тот же самый результат можно было получить, записав формулу (18.2) в виде системы уравнений
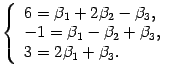
Решив эту систему, например, методом
Гаусса, найдем новые координаты
![]() ,
,
![]() ,
,
![]() .
.
Вперед: Матрица линейного преобразования Наверх: Линейные преобразования Назад: Линейные преобразования
Определение и примеры
Рассмотрим линейное
пространство
и
преобразование
![]() этого
пространства, то есть закон, по которому
каждому вектору
из
соответствует
вектор
этого
пространства, то есть закон, по которому
каждому вектору
из
соответствует
вектор
![]() из
того же пространства. Вектор
называется
образом
вектора
и
обозначается
из
того же пространства. Вектор
называется
образом
вектора
и
обозначается
![]() ,
а вектор
называется
прообразом
вектора
.
,
а вектор
называется
прообразом
вектора
.
Определение
19.1
Преобразование
линейного
пространства
называется
линейным,
если для любых векторов
и
![]() и
любого числа
и
любого числа
![]() выполнены
равенства
выполнены
равенства
|
(19.1) |
то есть образ суммы векторов равен сумме образов слагаемых, образ вектора, умноженного на число, равен произведению этого числа на образ вектора.
Замечание 19.1 В этой главе с каждым линейным преобразованием будет связана матрица, которую мы будем обозначать той же буквой, что и само преобразование. Чтобы их различать, мы для букв, обозначающих преобразование, будем использовать так называемый "каллиграфический" шрифт.
Линейное преобразование пространства называют также линейным отображением из в или линейным оператором из в .
Исходя из равенств (19.1) легко проверить, что
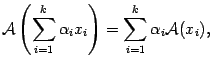
то есть образ линейной комбинации векторов равен линейной комбинации их образов.
Рассмотрим несколько примеров линейных преобразований.
Пример
19.1 Пусть
--
двумерное векторное пространство, то
есть множество векторов плоскости.
Пусть
![]() .
Это преобразование действует так: каждый
вектор оно переводит в вектор такого
же направления, но в два раза большей
длины. Если считать, что все векторы
имеют начало в начале координат, то
преобразование
можно
представить как растяжение плоскости
в два раза (рис. 19.1).
.
Это преобразование действует так: каждый
вектор оно переводит в вектор такого
же направления, но в два раза большей
длины. Если считать, что все векторы
имеют начало в начале координат, то
преобразование
можно
представить как растяжение плоскости
в два раза (рис. 19.1).
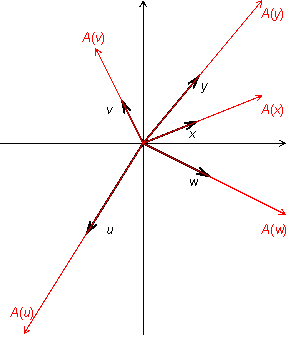
Рис.19.1.Преобразование растяжения
Проверим выполнение равенств (19.1)
![]()
![]()
Равенства (19.1) выполнены, следовательно, преобразование является линейным.
Пример
19.2 Пусть
--
двумерное векторное пространство,
--
поворот вектора по часовой стрелке на
угол
![]() (рис.
19.2).
(рис.
19.2).
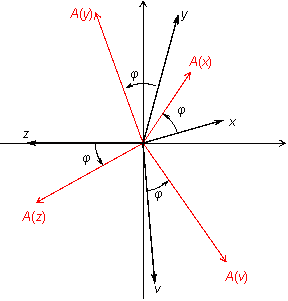
Рис.19.2.Преобразование поворота
Покажем, что это -- линейное преобразование.
Пусть
и
--
два вектора. Тогда
![]() --
это диагональ параллелограмма со
стронами
,
(рис.
19.3).
--
это диагональ параллелограмма со
стронами
,
(рис.
19.3).
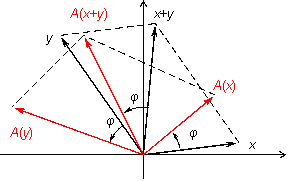
Рис.19.3.Образ суммы векторов
Если параллелограмм
повернуть как единое целое на угол
,
то его стороны станут векторами
и
![]() ,
диагональ будет вектором
,
диагональ будет вектором
![]() .
С другой стороны, диагональ тоже
повернулась на угол
и
поэтому является вектором
.
С другой стороны, диагональ тоже
повернулась на угол
и
поэтому является вектором
![]() .
Следовательно,
.
Следовательно,
![]() ,
первое из условий (19.1)
выполнено.
,
первое из условий (19.1)
выполнено.
Пусть
--
число. Из рисунка 19.4 очевидно, что
![]() .
.
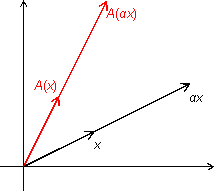
Рис.19.4.Образ вектора, умноженного на число
Следовательно, преобразование -- линейное.
Упражнение19.1.1.
Пусть
--
двумерное векторное пространство,
![]() --
некоторая прямая, проходящая через
начало координат,
--
преобразование, переводящее каждый
вектор
в
вектор
симметричный
исходному относительно прямой
(рис.
19.5). Другими словами,
является
зеркальным отражением вектора
в
прямой
.
--
некоторая прямая, проходящая через
начало координат,
--
преобразование, переводящее каждый
вектор
в
вектор
симметричный
исходному относительно прямой
(рис.
19.5). Другими словами,
является
зеркальным отражением вектора
в
прямой
.
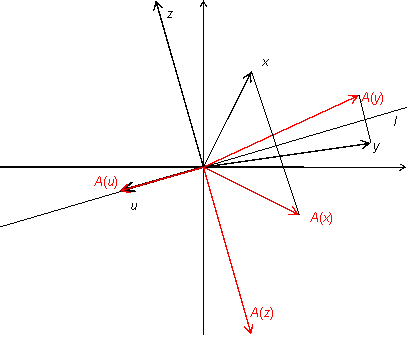
Рис.19.5.Преобразование отражения
Докажите, что является линейным преобразованием.
Упражнение19.1.2. Пусть -- двумерное векторное пространство, -- некоторая прямая, проходящая через начало координат, -- преобразование, переводящее каждый вектор в его проекцию на прямую (рис. 19.6).
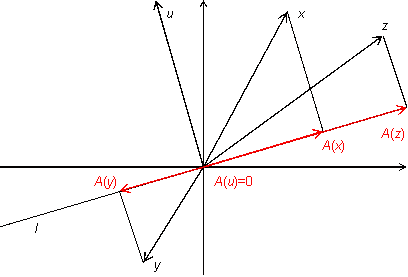
Рис.19.6.Преобразование проектирования
Докажите, что является линейным преобразованием.
Пример
19.3 Пусть
--
пространство всех многочленов,
--
преобразование, которое переводит
вектор из
,
то есть многочлен, в производную этого
многочлена, которая естественно является
многочленом, то есть вектором из
.
Пусть
![]() ,
то есть
,
то есть
![]() .
Тогда
.
Тогда
![]()
Например, если
![]() ,
то
,
то
![]() .
Покажем, что преобразование
является
линейным.
.
Покажем, что преобразование
является
линейным.
Пусть
![]() ,
--
число. Тогда в силу свойства линейности
производной получим
,
--
число. Тогда в силу свойства линейности
производной получим
![]()
Аналогично,
![]()
Следовательно, -- линейное преобразование.
Пример
19.4 Пусть
--
-мерное
линейное пространство, Выберем в этом
пространстве базис
.
Тогда у любого вектора
есть
его координатный столбец
 .
Пусть
--
квадратная матрица порядка
.
Определим преобразование
следующим
образом:
.
Пусть
--
квадратная матрица порядка
.
Определим преобразование
следующим
образом:
![]() является
вектором, координатный столбец которого
равен
является
вектором, координатный столбец которого
равен
![]() (справа
стоит произведение матрицы
на
столбец
).
Покажем, что преобразование
--
линейное.
(справа
стоит произведение матрицы
на
столбец
).
Покажем, что преобразование
--
линейное.
Пусть
и
имеют
координатные столбцы
и
![]() соответственно,
а их образы
и
--
координатные столбцы
,
и
соответственно,
а их образы
и
--
координатные столбцы
,
и
![]() .
Тогда
.
Тогда
![]()
Но выражение в
последнем равенстве справа является
координатным столбцом образа суммы
векторов
.
Следовательно,
![]() .
.
Пусть
![]() --
произвольное число. Тогда координатный
столбец вектора
--
произвольное число. Тогда координатный
столбец вектора
![]() равен
равен
![]() ,
координатный столбец образа вектора
,
координатный столбец образа вектора
![]()
то есть равен числу
,
умноженному на координатный столбец
образа вектора
.
Поэтому
![]() .
Тем самым мы доказали, что преобразование
является
линейным.
.
Тем самым мы доказали, что преобразование
является
линейным.
Очевидно, что
примерами линейных преобразований
могут служить тождественное
преобразование,
то есть преобразование, переводящее
каждый вектор в себя,
![]() ,
и нулевое
преобразование,
переводящее каждый вектор в нуль,
,
и нулевое
преобразование,
переводящее каждый вектор в нуль,
![]() .
.
Легко проверяется,
что для любого линейного преобразования
образ
нуля равен нулю,
![]() .
Действительно, в силу второго из
равенств (19.1)
.
Действительно, в силу второго из
равенств (19.1)
![]()
Вперед: Матрица линейного преобразования Наверх: Линейные преобразования Назад: Линейные преобразования
Вперед: Координаты векторов Наверх: Линейные пространства Назад: Определение и примеры