Вариант 17.

№13.

В прямоугольной трапеции ABCD высота АВ равна сумме оснований AD и ВС. Биссектриса угла АВС пересекает сторону CD в точке К. В каком отношении эта точка делит CD?

Д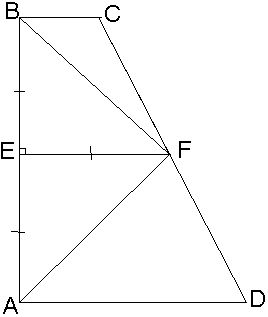 ано: ABCD – прямоугольная трапеция, , - биссектриса, .

Найти:

Решение.

I способ

Пусть EF – средняя линия ABCD. Проведем BF и AF, , также - равнобедренный, ;

- биссектриса, - средняя линия и

Ответ:

I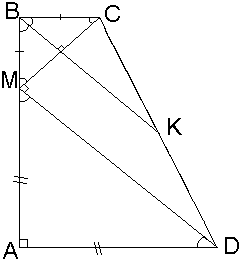 I способ

Пусть , тогда - равнобедренный

также равнобедренный

- прямоугольный

ВК – биссектриса равнобедренного треугольника с основанием МС ВК – серединный перпендикуляр к центр описанной вокруг окружности лежит на ВК, но он также лежит на CD, как на гипотенузе. В , точка, принадлежащая одновременно CD и ВК, является точкой К К – центр описанной вокруг окружности .

Ответ:

I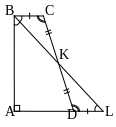 I способ

Пусть BK  AD = L. Так как BK – биссектриса B, а B = 90, то ABL = = CBL = 45. Так как AL װ BC, то BCD = CDL, ABL = CBL = L = = 45  ABL – равнобедренный  AB = AL. Так как AB = AD + BC, AL = = AD + DL, а AB = AL, то AD + BC = AD + DL  BC = DL. Так как BCD = = CDL, CBL = L, BC = DL, то BCK = DKL  CK = KD  .

Ответ:

№14.

В окружность диаметра см вписан шестиугольник, одна сторона которого 10 см, а все остальные равны между собой. Найдите его углы.

Д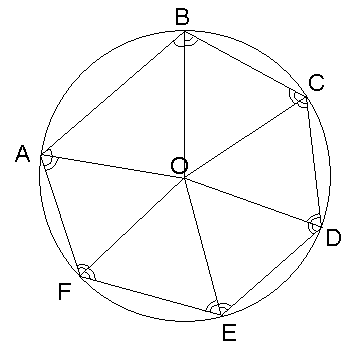 ано: , , .

Найти:

Решение.

I способ

по теореме косинусов

Ответ: ,

I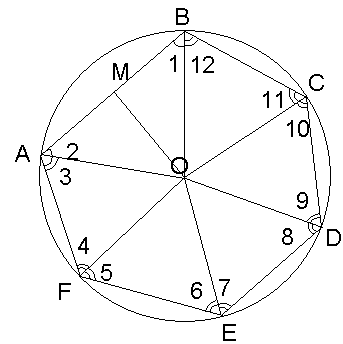 I способ

Пусть . В - равнобедренный

Сумма всех углов шестиугольника

Итак ,

Ответ: ,

№15.

На окружности с центром О дана точка А. найдите геометрическое место середин всех хорд этой окружности, проведенных из точки А.

Д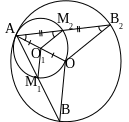 ано: , ,

Найти: ГМТ точки М

Решение.

Пусть точка B₁ окружности такая, что точка O не лежит на отрезке AB₁. Пусть O₁ – середина AO. Тогда, поскольку M₁ – середина AB₁ и O₁ – середина AO, O₁M₁ – средняя линия в AOB₁  O₁M₁ = ½OB₁ = ½R. Таким образом, точка M₁ удалена от данной точки O₁ на данное расстояние, равное ½R. Тогда, в силу произвольности выбора точки B₁, все точки M лежат на данном расстоянии от точки O₁, то есть, на окружности с центром в точке O₁ и радиусом, равным ½R. Докажем, что все точки этой окружности принадлежат искомому ГМТ. Выберем произвольно точку M₂ этой окружности. Пусть прямая AM₂ пересекает данную окружность в точке B₂. Докажем, что M₂ – середина AB₂. Так как AO = OB₂, то AOB₂ – равнобедренный  OAB₂ = OB₂A. Также AO₁ = O₁M₂, поэтому AO₁M₂ – равнобедренный  OAB₂ = O₁M₂A  OB₂A = O₁M₂A  O₁M₂ װ OB₂, а так как O₁ – середина AO, то по теореме Фалеса M₂ – середина AB₂. Итак, искомое ГМТ – окружность с центром в середине отрезка AO и радиусом, равным половине этого отрезка.

Ответ:

Вариант 18.

№ 13.

Найдите радиус окружности, описанной около равнобедренного треугольника с основанием 10 см и боковой стороной 13 см.

Д ано: ABC, AB = AC = 13, BC = 10.

Найти: R

Решение.

S_ =

R = .

Ответ:

№ 14.

Точки M и N – середины сторон CD и BC параллелограмма ABCD. Докажите, что отрезки AM и AN делят диагональ BD на три равные части.

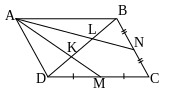
Дано: ABCD – параллелограмм, MС=MD, NB=NC, AMBD = K, ANBD = L

Доказать: DK = KL = LB

Доказательство.

Так как ABCD – параллелограмм, то AB = DC, AD = BC, AB║CD, AD║BC. Так как M – середина CD, то DM = ½CD = ½AB  Аналогично . Так как AB║CD, то ABK ~ DKM     DK = BD – DK  DK = BD  DK = BD. Аналогично из подобия треугольников ALD и BLN получаем: BL = BD. Так как DK + KL + LB = = BD, DK = BD, BL = BD, то и KL = BD  DK = KL = LB, ч.т.д.

№ 15.

На гипотенузе AB прямоугольного треугольника ABC выбрана произвольная точка M, и из неё опущены перпендикуляры MK и MP на катеты этого треугольника. Определите, при каком положении точки M длина отрезка PK будет наименьшей.

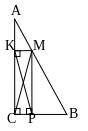
Дано: ABC, C = 90, M AB, MK  AC, MP  BC

Найти: при каком положении точки M длина отрезка PK будет наименьшей.

Решение.

Заметим, что CKMP – прямоугольник  PK = CM при любом положении точки M на гипотенузе. Значит PK минимально только в том случае, если CM минимально, а минимальное расстояние от точки C до прямой AB есть отрезок перпендикуляра, опущенного из точки C на прямую AB. Значит M – основание высоты, опущенной из вершины C на гипотенузу.

Ответ: M – основание высоты, опущенной из вершины C на гипотенузу.