Вариант 15

№ 13.

В треугольнике ABC биссектриса AE равна отрезку EC. Найдите углы треугольника ABC, если известно, что AC = 2AB.

Д ано: ABC, AE – биссектриса BAC, AE = EC, AC = 2AB

Найти: A, C, B

Решение.

Так как AE – биссектриса A, то BAE = CAE. Так как AE = EC, то AEC – равнобедренный  BAE = CAE = C  A = 2C. Пусть M – середина AC. Тогда AB = AM = MC, поскольку AC = 2AB,  EM – медиана AEC, а так как AEC равнобедренный, то EM – высота AEC  AME = 90. Так как по условию AC=2AB и М – середина АС, то AB = AM=МС, BAE = CAE, AE – общая сторона, то ABE = AME  B = AME = 90. A + B + C = 180, а так как B = 90, A = 2C, то 3C = 90  C = 30  A = 60.

Ответ: A = 60, C = 30, B = 90.

№ 14.

В равнобокую трапецию с острым углом 30 вписана окружность. Найдите отношение длины окружности к периметру трапеции.

Дано: ABCD – равнобокая трапеция с основаниями AD и BC, A = D = = 30, Окр.(О;r) - вписанная

Найти:

Решение.

Пусть BH – высота трапеции. Тогда BH = 2r, где r – радиус окружности. Поскольку трапеция является описанной около окружности, то AB+CD = BC + AD, а так как AB = CD (трапеция равнобокая), то AB = .

Так как ABH – прямоугольный, а A = 30, то BH = . ,   .

Ответ:

№ 15.

Внутри треугольника ABC взята точка D такая, что ABD = ACD = 45. Докажите, что отрезки AD и BC перпендикулярны и равны, если угол BAC равен 45.

Д ано: ABC, A = 45, D ABC, ABD = ACD = 45

Доказать: AD = BC, AD BC

Доказательство.

Пусть BD  AC = B₁, CD  AB = C₁, AD  BC = A₁. Тогда BB₁  AC, поскольку AB₁B = 180 - A - ABD = 90,  BB₁ – высота ABC. Аналогично CC₁ – высота ABC  D – точка пересечения высот ABC  AA₁ – высота ABC  AD  BC. Так как ABB₁ – равнобедренный, то AB₁ = BB₁. Также B₁DC – равнобедренный, поэтому B₁D = B₁C. Тогда треугольники AB₁D и BB₁C равны по двум катетам  AD = BC, ч.т.д..

Вариант 16.

№13.

В трапеции ABCD диагонали АС и BD перпендикулярны. На большем основании AD выбрана точка М так, что ВМ=MD=3 см. Найдите длину средней линии трапеции.

Д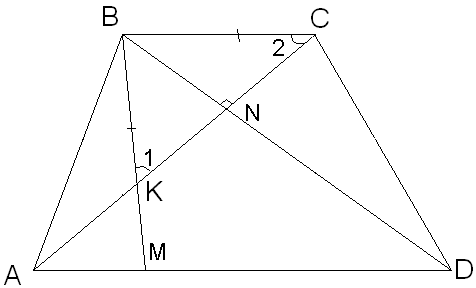 ано: ABCD – трапеция, , ВМ=MD=3 см.

Найти:

Решение.

I способ

Т.к. ВМ=MD, то - равнобедренный

как накрест лежащие при и секущей BD.

BN –биссектриса и высота - равнобедренный и ВК=ВС , KN=NC

как накрест лежащие при и секущей АD,

, т.е.

Ответ:

I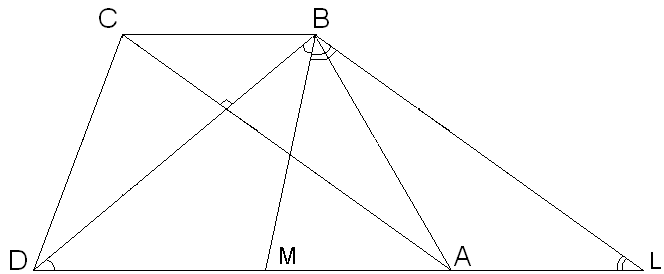 I способ

Дополнительное построение:

LBCA – параллелограмм ( )

. - равнобедренный . Также , - равнобедренный длина ВМ численно равна длине средней линии трапеции и ВМ=3см

Ответ:

I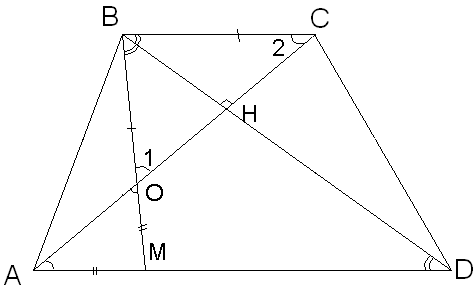 II способ

Т.к. ВМ=MD, то - равнобедренный

как накрест лежащие при и секущей BD.

BН –биссектриса и высота - равнобедренный и ВК=ВС , ВС=ВО

Пусть ВС=ВО=х, тогда ОМ=3-х

( как накрест лежащие при и секущей АС), значит, - равнобедренный АМ=ОМ=3-х

Ответ:

№14.

Найдите углы треугольника, если высота и медиана, проведенные из одной вершины, делят угол при этой вершине треугольника на три равные части.

Д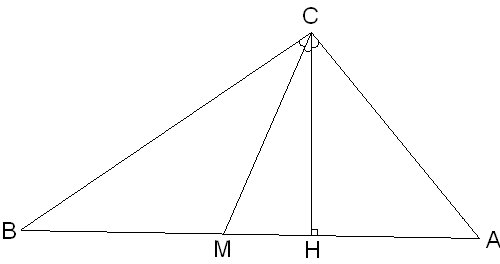 ано: , медиана СМ, СН - высота,

Найти: A, C, B

Решение.

: СН – биссектриса, тогда, по свойству биссектрисы угла треугольника,

Тогда

Ответ: ,

№ 15.

Две окружности пересекаются в точках A и B, прямая CD – общая касательная этих окружностей (C и D – точки касания). Прямые AB и CD пересекаются в точке N. Докажите, что N – середина CD.

Дано: ₁ и ₂ – окружности, ₁   ₂ = {A;B}, CD – общая касательная, CD  ₁ = C, CD  ₂ =D, AB  CD = N

Доказать: CN = ND

Доказательство.

По теореме о квадрате касательной для окружности ₁ имеем: . Аналогично, для окружности ₂ получаем: . Значит CN² = ND²  CN = ND  N – середина CD, ч.т.д.