
- •Введение.
- •Основные факты планиметрии.
- •I. Треугольники
- •1) Теорема синусов.
- •2) Теорема косинусов.
- •3) Теорема о биссектрисе угла в треугольнике.
- •4) Вычисление биссектрисы угла.
- •5 ) Вычисление координаты точки отрезка.
- •4 ) Теорема об отрезках пересекающихся хорд.
- •Вариант 1.
- •Вариант 2.
- •Вариант 4.
- •Вариант 5.
- •Вариант 6.
- •Вариант 7.
- •Вариант 8.
- •Вариант 9.
- •Вариант 10.
- •Вариант 11.
- •Вариант 12.
- •Вариант 13.
- •Вариант 14.
- •Вариант 15
- •Вариант 16.
- •Вариант 17.
- •Вариант 18.
- •Вариант 19.
- •Вариант 20.
Вариант 10.
№13.
В выпуклом четырехугольнике ABCD
точки Е, F и G
– середины сторон АВ, ВС и AD
соответственно, причем
![]() .
Найдите угол ACD.
.
Найдите угол ACD.
Д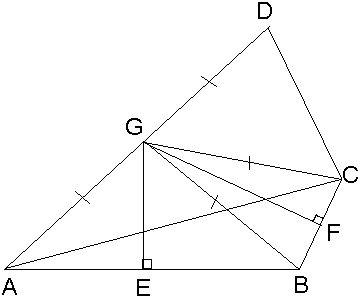 ано:
ABCD – выпуклый четырехугольник,
ано:
ABCD – выпуклый четырехугольник,
![]() .
.
Найти:
![]()
Решение.
GF – серединный перпендикуляр
к
![]() ,
GЕ – серединный перпендикуляр
к
,
GЕ – серединный перпендикуляр
к
![]() ,
значит, точка G равноудалена
от всех вершин ABCD
G
– центр описанной около ABCD
окружности.
,
значит, точка G равноудалена
от всех вершин ABCD
G
– центр описанной около ABCD
окружности.
опирается на диаметр![]()
Ответ:
![]()
№14.
В треугольник вписан ромб так, что один угол у них общий, а противоположная вершина делит сторону треугольника в отношении 1:3. Диагонали ромба равны 18 см и 24 см. Найдите стороны треугольника, содержащие стороны ромба.
Д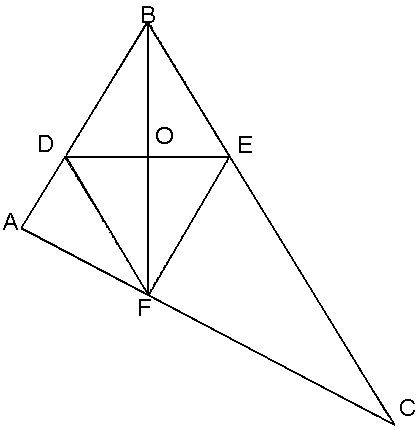 ано:
DBFE – ромб,
ано:
DBFE – ромб,
![]() ,
,
![]() ,
,
![]() .
.
Найти: АВ, ВС
Решение.
Т.к. DBFE – ромб, то, из
прямоугольного
![]() .
.
![]() и аналогично
и аналогично
![]() ,
тогда
,
тогда
![]() и
и
![]() ,
как соответственные углы при параллельных
прямых, значит,
,
как соответственные углы при параллельных
прямых, значит,
![]()
![]()
![]()
Ответ:
![]() ,
,
![]()
№15.
Две противоположные стороны выпуклого четырехугольника лежат на перпендикулярных прямых. Докажите, что расстояние между серединами двух других сторон четырехугольника равно расстоянию между серединами его диагоналей.
Д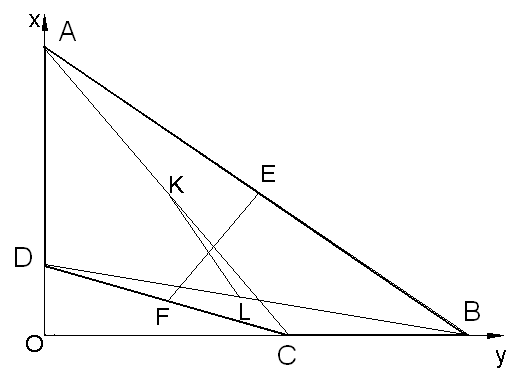 ано:
ABCD – выпуклый четырехугольник,
ано:
ABCD – выпуклый четырехугольник,
![]() .
.
Доказать: BF=KL
Доказательство.
Зададим прямоугольную систему координат так, что сторона СВ лежит на оси Ox, AD - на Oy, тогда пусть A(0;a), B(b;0), C(c;0), D(0;d).
Тогда
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]()
![]()
Т.е. BF=KL, ч.т.д.
Вариант 11.
№13.
В параллелограмме ABCD диагональ BD перпендикулярна стороне AD. Найдите АС, если AD=6 см и BD=5 см.
Д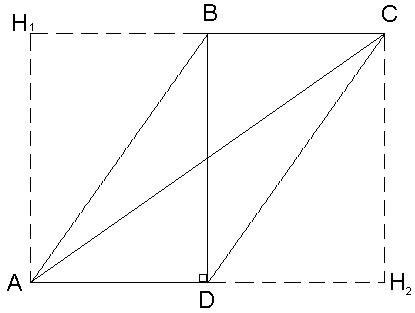 ано:
ABCD – параллелограмм,
ано:
ABCD – параллелограмм,
![]() ,
,
![]() .
.
Найти: АС
Решение.
Дополнительное построение:
![]() ,
так что
,
так что
![]() и
и
![]() поэтому
поэтому
![]() ,
,
![]() Т.е. получим прямоугольник
Т.е. получим прямоугольник
![]() ,
где
,
где
![]() ,
,
![]() .
Из прямоугольного
.
Из прямоугольного
![]() :
:
![]()
Ответ:
![]()
№14.
В шестиугольнике ABCDEF AB=AF, BC=CD, DE=EF. Докажите, что биссектрисы углов А, С и Е пересекаются в одной точке.
Д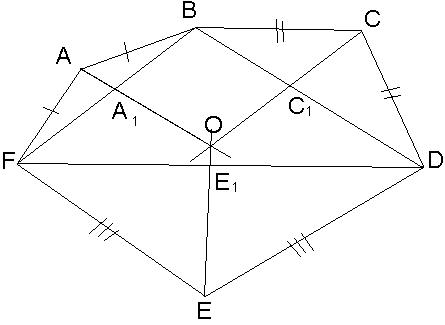 ано:
ABCDEF, AB=AF,
BC=CD, DE=EF,
АА1, СС1, ЕЕ1 - биссектрисы.
ано:
ABCDEF, AB=AF,
BC=CD, DE=EF,
АА1, СС1, ЕЕ1 - биссектрисы.
Доказать:
![]()
Доказательство.
![]() - равнобедренные, тогда АА1, СС1,
ЕЕ1 – биссектрисы и медианы
- равнобедренные, тогда АА1, СС1,
ЕЕ1 – биссектрисы и медианы![]() - серединные перпендикуляры к сторонам
- серединные перпендикуляры к сторонам
![]() ,
а серединные перпендикуляры пересекаются
в треугольнике в одной точке, т.е.
,
ч.т.д.
,
а серединные перпендикуляры пересекаются
в треугольнике в одной точке, т.е.
,
ч.т.д.
№15.
Две стороны треугольника имеют длины
6 см и 12 см, а угол между ними равен
![]() .
Найдите длину биссектрисы, проведенной
к большей стороне.
.
Найдите длину биссектрисы, проведенной
к большей стороне.
Д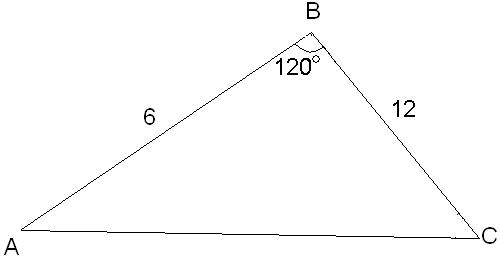 ано:
,
ано:
,
![]() ,
,
![]() .
.
Найти: длину биссектрисы, проведенной к большей стороне.
Решение.
По теореме косинусов
![]()
![]() ,
т.е.
,
т.е.
![]() искомая
биссектриса
,
т.к. против большего угла лежит большая
сторона
искомая
биссектриса
,
т.к. против большего угла лежит большая
сторона
![]()
Ответ:
![]()
Вариант 12.
№13.
В треугольнике со сторонами 30 см, 25 см и 11 см найдите длину высоты, проведенной из вершины меньшего угла.
Д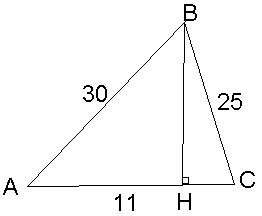 ано:
,
ано:
,
![]() .
.
Найти: длину высоты, проведенной из вершины меньшего угла.
Решение.
Дополнительное построение:
Меньший угол лежит против меньшей
стороны![]() - меньший.
- меньший.
Пусть
![]() ,
тогда из
,
тогда из
![]() :
:
![]()
Из
![]() ,
,
![]()
![]()
![]()
Ответ:
![]()
№14.
Найдите площадь равнобокой трапеции, если ее диагональ равна 29 см, а средняя линия – 21 см.
Д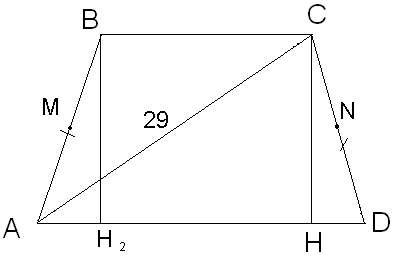 ано:
ABCD – равнобокая трапеция,
ано:
ABCD – равнобокая трапеция,![]() ,
,
![]() -
средняя линия,
-
средняя линия,
![]() .
.
Найти:
Решение.
Дополнительное построение:
![]() .
.
Т.к.
![]() ,
то
,
то
![]()
![]()
![]() - прямоугольный,
- прямоугольный,
![]()
![]()
Ответ:
![]()
№15.
Найдите геометрическое место середин всех хорд данной окружности, имеющих заданную длину.
Д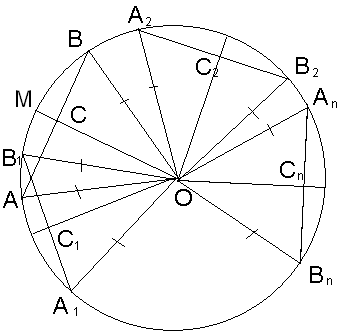 ано:
,
ано:
,
![]() -
хорды,
-
хорды,
![]() - середины хорд
- середины хорд
Найти: ГМТ
Решение.
![]() ,
т.к.
,
т.к.
![]() ,
,
![]() (
по теореме о диаметре, делящем хорду
пополам),
(
по теореме о диаметре, делящем хорду
пополам),
![]()
Тогда
![]() ,
т.е. середины хорд равноудалены от центра
окружности, т.е. лежат на окружности с
центром в точке О и
,
т.е. середины хорд равноудалены от центра
окружности, т.е. лежат на окружности с
центром в точке О и
![]() .
.
Теперь докажем, что все точки окружности
![]() являются серединами хорд данной
окружности длины l.
являются серединами хорд данной
окружности длины l.
Пусть
![]() .
Построим
.
Построим
![]() ,
т.е. АВ – касательная к окружности
.
,
т.е. АВ – касательная к окружности
.
![]() (
(![]() - общая, AO=OB=R).
По теореме Пифагора
- общая, AO=OB=R).
По теореме Пифагора
![]() ,
ч.т.д.
,
ч.т.д.
Ответ: середины хорд лежат на
окружности с центром в точке О и
![]() .
.
