Вариант 4.
№13.
Две касающиеся окружности с центрами О1 и О2 лежат внутри окружности с центром О и радиусом R касаются ее в двух различных точках. Найдите периметр треугольника ОО1О2.
Д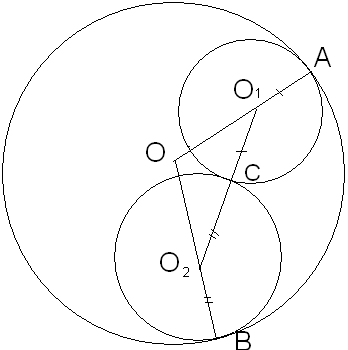
ано:
Окр. (О; R), Окр(О1;r),
Окр(О2;R`) –касаются
друг друга.
Найти:
Решение.
Известно, что точка касания двух
окружностей лежит на прямой, соединяющей
их центры, тогда
и
,
и
- лежат на одних и тех же прямых.
Пусть А, В, С – точки касания окружностей,
тогда
(т.к.
)
(т.к.
)
Но
Ответ:
№14.
Треугольник АВС, стороны которого 13 см, 14 см и 15 см, разбит на три треугольника отрезками, соединяющими точку пересечения медиан М с вершинами треугольника. Найдите площадь треугольника ВМС.
Д
ано:
,
- медианы,
см,
см,
см
Найти:
Решение.
,
,
т.к.
,
высота общая
,
аналогично
По формуле Герона
Ответ:
см2
№15.
Каждая высота параллелограмма не меньше той стороны, которой она перпендикулярна. Докажите, что параллелограмм является квадратом.
Д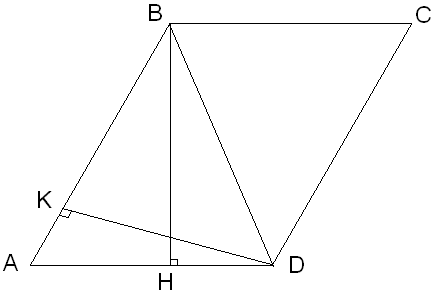
ано:
ABCD – параллелограмм,
,
,
,
.
Доказать: ABCD - квадрат
Доказательство.
Рассмотрим 2 случая:
1)
,
(т.к.
AD – гипотенуза прямоугольного
треугольника AKD)
С другой стороны
-
получено противоречие, значит, утверждение
не верно и
,
2) Итак,
,
,
т.е.
,
- квадрат, ч.т.д.
Вариант 5.
№13.
В равнобокой трапеции, площадь которой
равна
см2, одно из оснований в
два раза больше другого. Диагональ
трапеции является биссектрисой острого
угла. Найдите основания трапеции.
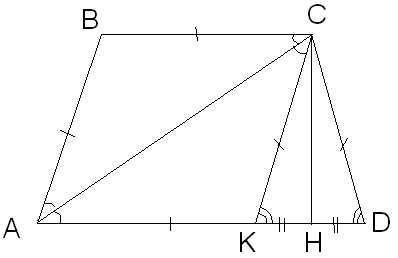
Дано: ABCD – трапеция,
,
,
АС – биссектриса
.
Найти:
Решение.
Дополнительное построение:
.
-
равносторонний и
Дополнительное построение:
,
т.к.
равносторонний, то СН – высота, медиана
и биссектриса.
- прямоугольный,
Ответ:
№14.
Точки С и D лежат на окружности с диаметром АВ. Прямые AC и BD пересекаются в точке Р, а прямые AD и BС – в точке Q. Докажите, что прямые AB и PQ перпендикулярны.
Д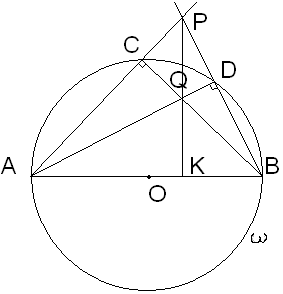
ано:
,
,
,
AC
BD=Р,
AD
BС=Q
Доказать:
Доказательство.
и
-
прямоугольные, т.к. опираются на диаметр.
Рассмотрим
:
- точка пересечения высот
,
а т.к. она единственна, то
,
ч.т.д.
№15.
Прямая проходит через центр квадрата со стороной 1. Найдите сумму квадратов расстояний от всех вершин квадрата до этой прямой.
Д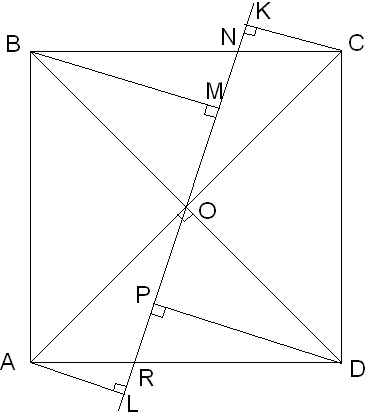
ано:
ABCD – квадрат,
,
.
Найти:
Решение.
,
-прямоугольные,
,
-
общий, тогда
,
значит,
=
(по
углу и гипотенузе), тогда
.
Аналогично
,
значит,
Ответ:
Вариант 6.
№13.
В прямоугольном треугольнике АВС
проведена высота CD
к гипотенузе АВ. Найдите АВ, если
.
Д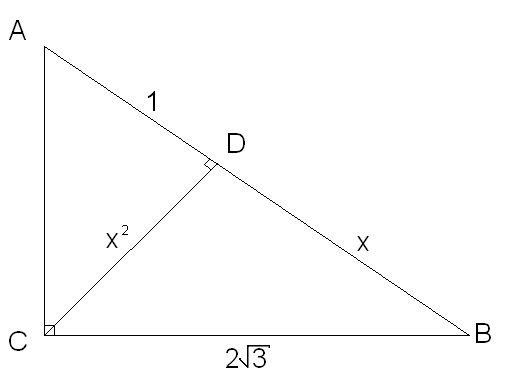
ано:
- прямоугольный, CD –
высота,
Найти: АВ
Решение.
Пусть
,
тогда
,
т.е.
Ответ:
№14.
На стороне АВ параллелограмма ABCD как на диаметре построена окружность, проходящая через точку пересечения диагоналей и середину стороны AD. Найдите углы параллелограмма.
Дано: ABCD – параллелограмм,
,
,
,
AC
BD=О,
Найти:
Решение.
,
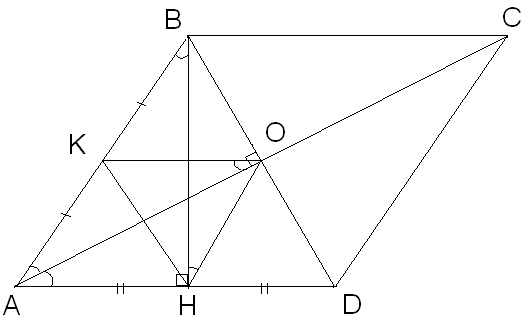т.к. О – середина BD, К –
середина АВ
КО
– средняя линяя
,
аналогично
,
как углы, опирающиеся на диаметр
,
т.к. они опираются на одну дугу
,
т.к.
,
как накрест лежащие при
и секущей АО
Тогда
(из
)
Ответ:
№15.
Каждая диагональ четырехугольника делит его на два равновеликих треугольника. Докажите, что данный четырехугольник – параллелограмм.
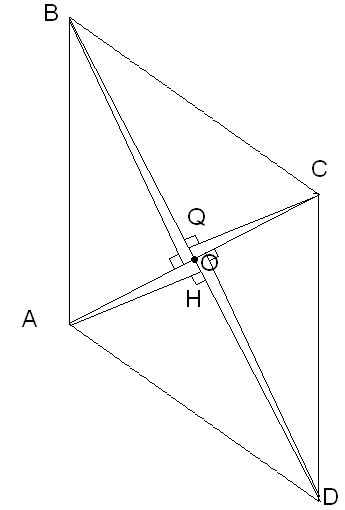Дано:
ABCD – четырехугольник,
AC
BD=О,
Доказать: ABCD – параллелограмм
Доказательство.
Дополнительное построение:
.
Т.к.
BD – общая, то
,
,
как вертикальные углы,
Аналогично
,
аналогично
- параллелограмм, ч.т.д.