Решебник к сборнику заданий А.Д.Блинкова, Т.М.Мищенко
для проведения экзамена по геометрии
в 9 классе
(задания второй части итоговой аттестационной работы).
Комсомольск-на-Амуре
2008 год
Учебное пособие составлено на основе решений учащихся МОУ лицей №1 г.Комсомольска – на – Амуре Замана К. и Мельниченко А. под руководством Будлянской Н.Л., учителя математики высшей категории.
В пособии приведены решения задач второй части итоговой аттестационной работы по геометрии в 9 классе. Все решения задач изложены очень грамотно и четко с необходимыми пояснениями. Для задач представлены по 2-3 способа решения. Некоторые задачи сборника сформулированы таким образом, что необходимо рассмотреть различные варианты предложенной в условии задачи ситуации (задача №15 варианта 2), и это отмечено в их решении.
Данный сборник решенных задач представляет определенную значимость для учителей и учащихся 9 класса при подготовке к экзамену по геометрии.
Заслуженный учитель школы РФ
кандидат педагогических наук,
доцент Г.Н.Сумина
2008г.
Введение.
При подготовке к итоговой аттестации по геометрии в 9 классе многие учителя и учащиеся используют «Сборник заданий для проведения экзамена в 9 классе» авторов А.Д.Блинкова и Т.М.Мищенко, издательства «Просвещение», 2006. При этом задачи второй части вызывают у некоторых серьезные затруднения, что усугубляется отсутствием ответов и комментариев к ним.
Данное пособие призвано помочь снять эти трудности.
Пособие снабжено описанием используемых основных теоретических фактов, необходимыми чертежами и пояснениями. Многие задачи решены несколькими способами.
Основные факты планиметрии.
I. Треугольники
1) Теорема синусов.
В треугольнике стороны пропорциональны синусам противолежащих
углов.
В
а b
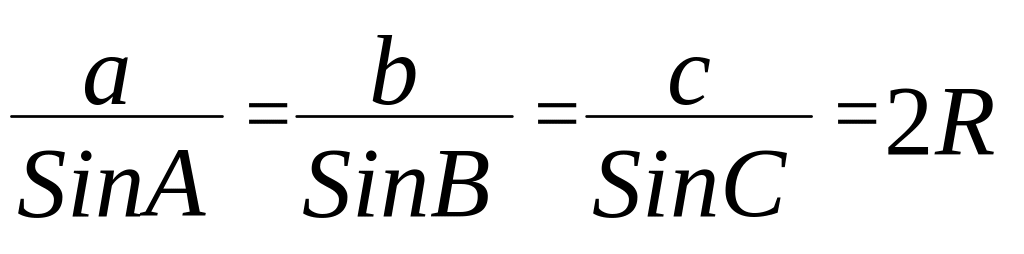
А c С
2) Теорема косинусов.
В треугольнике квадрат одной стороны равен сумме квадратов двух других
сторон без удвоенного произведения этих сторон на косинус угла между
ними.
В
а b
А с С
Примечание. Если CosA
0,
то
А
– острый, если CosА
= 0, то
А
– прямой, если CosA
0,
то
А
– тупой.
3) Теорема о биссектрисе угла в треугольнике.
Биссектриса угла треугольника делит его сторону на части,
пропорциональные прилежащим сторонам.
В
D
А С
4) Вычисление биссектрисы угла.
В
А
С
5 ) Вычисление координаты точки отрезка.
С В
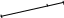А
,
где
или
,
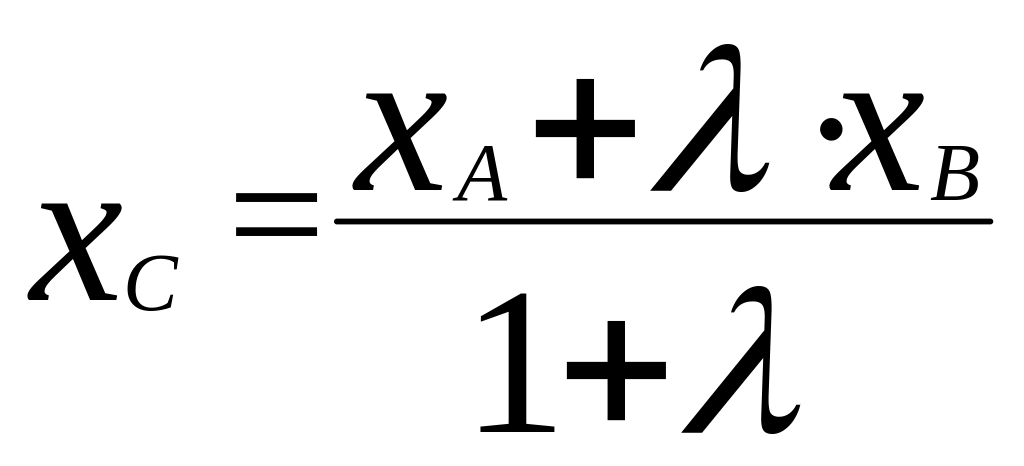где
6) Теорема о медианах.
В треугольнике медианы пересекаются в одной точке и делятся в
отношении 2:1, считая от вершины.
В
А
С
7) Вычисление длины медианы треугольника
С
с
а 
А b В
8) Теорема о высоте прямоугольного треугольника.
С
b a
,
где
=DB
– проекция катета а
на
гипотенузу с,
=АD
– проекция
А c В катета b на гипотенузу с.
D
,
9) Теорема о центре вписанной окружности.
В
Центр вписанной окружности лежит на
пересечении биссектрис треугольника.
А С
10) Теорема о центре описанной окружности.
Центр описанной окружности лежит на пересечении серединных
Перпендикуляров к сторонам треугольника.
Центр описанной окружности в остроугольном треугольнике лежит внутри треугольника;
Центр описанной окружности в тупоугольном треугольнике лежит вне треугольника;
Центр описанной окружности в прямоугольном треугольнике лежит на середине гипотенузы.
11) Тригонометрические функции в прямоугольном
треугольнике.
А
,
,
,
b с
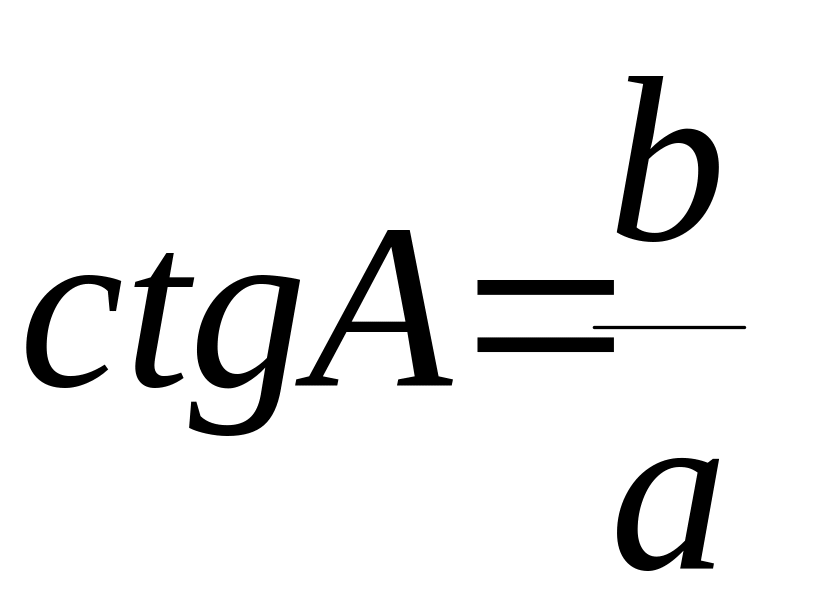
С В
а
12) Площадь треугольника.
а)
;
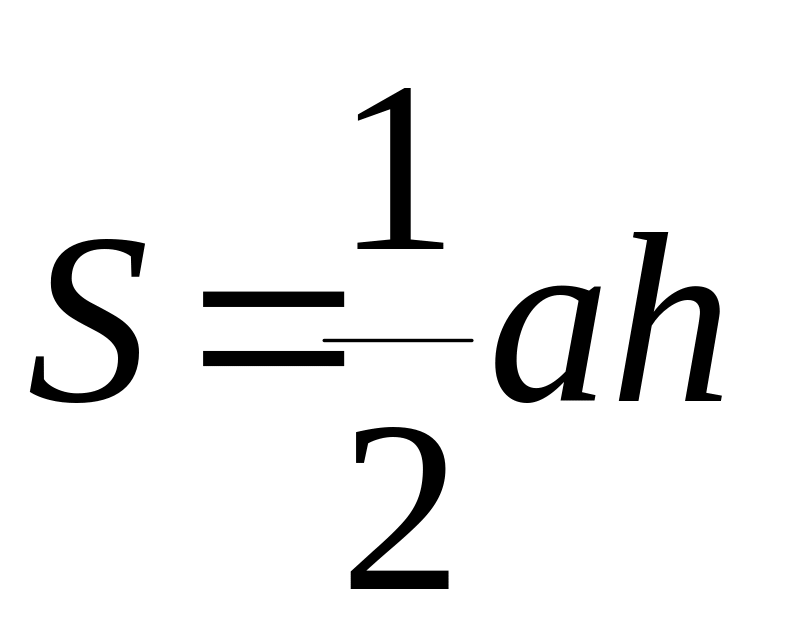б)
;
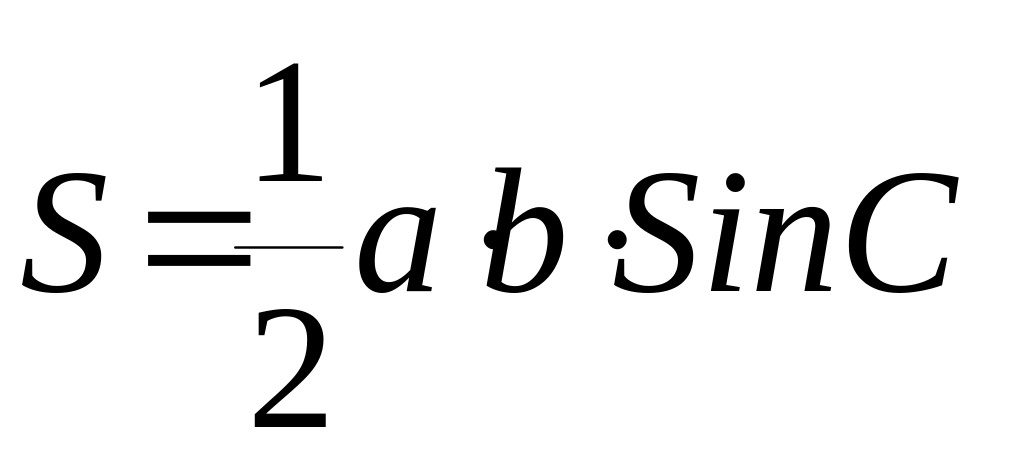в)
,
где
;
г)
,
где R – радиус
описанной окружности;
д)
;
е)
,
где r радиус
вписанной окружности, Р –
периметр
треугольника;
ж)
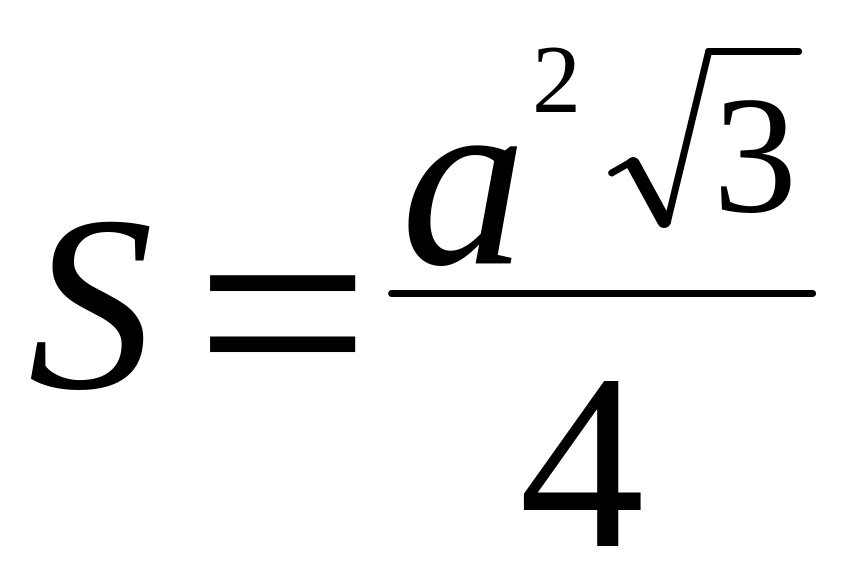- площадь равностороннего треугольника;
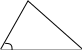
13) Теорема об отношении площадей треугольников, имеющих равный угол.
В
А С
Площади относятся как произведение
сторон, заключающих равные углы, то есть
если
,
то
.
14) Теорема об отношении площадей подобных треугольников.
В
А С
,
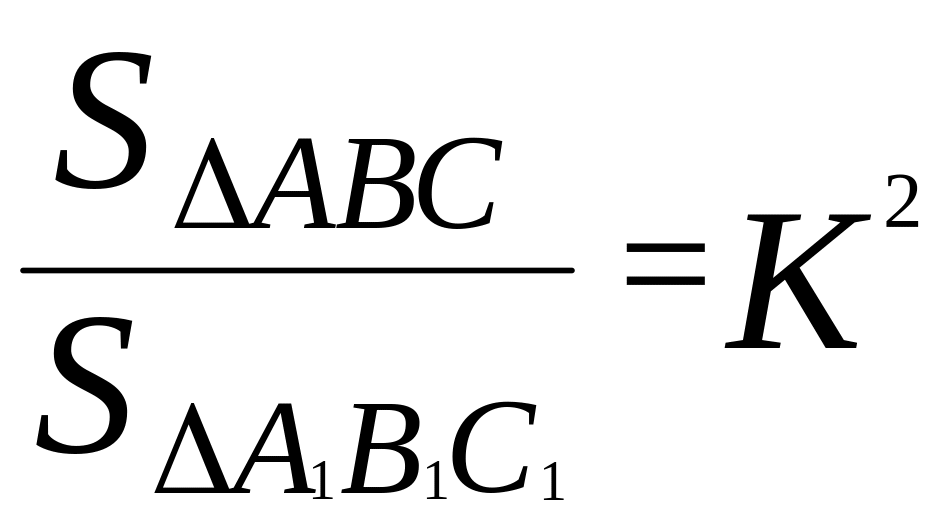где К – коэффициент подобия.
Примечание:
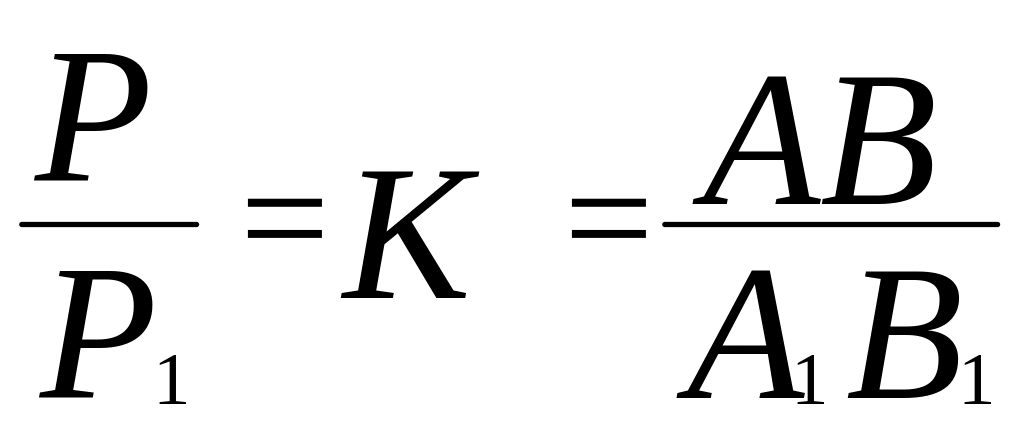
14) Теорема Чевы.
Если три чевианы пересеклись в одной точке, то
В
,
,
- чевианы.
А С
II. Четырехугольники
1) Параллелограмм.
В а С
h
площадь
b
параллелограмма АВСD
А D
В С
A D
где
и
-
диагонали параллелограмма АВСD
2) Ромб.
В
,
где
и
-
диагонали ромба АВСD
А С
,
где а – сторона ромба
D
3) Трапеция.
B b
C 
,
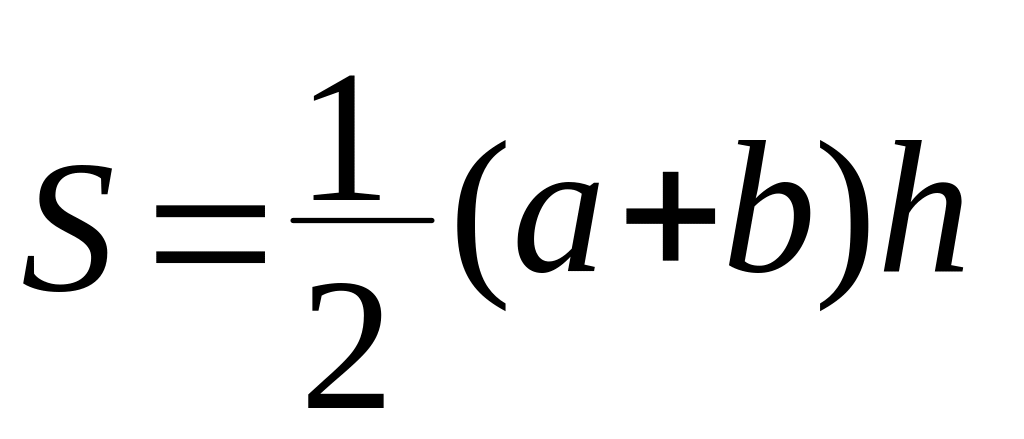
где
-
средняя линия трапеции
A а D
4) Свойства описанного четырехугольника.
b
В любом описанном четырехугольнике
суммы противо-
положных сторон равны:
a c
с
d
5) Свойства вписанного четырехугольника.
В любом вписанном четырехугольнике сумма
противоположных
углов равна
:
6) Площадь любого четырехугольника, у которого диагонали
перпендикулярны, выражается формулой:
В
А С , где и - диагонали
D четырехугольника АВСD.
7) Правильные многоугольники.
-
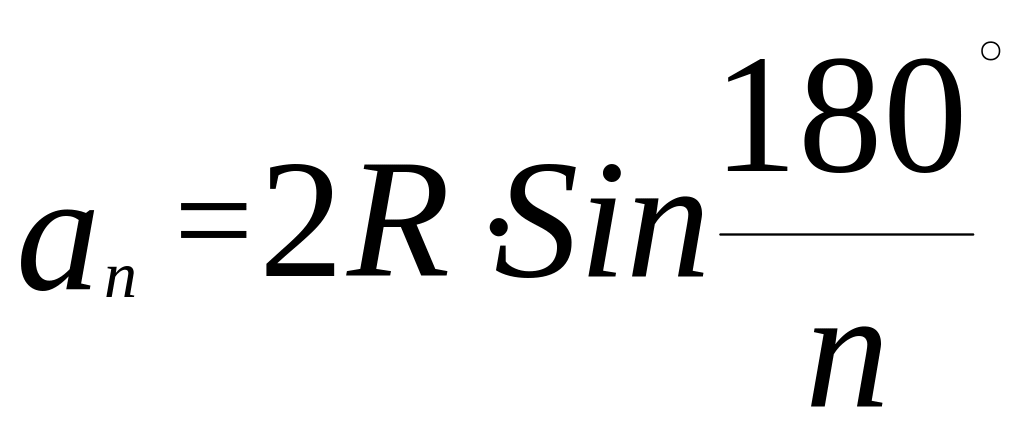сторона правильного многоугольника,
где R – радиус описанной окружности;
- сторона правильного многоугольника,
где – r радиус
вписанной окружности;
I
II.
Окружность.
1)
В
АВС
– вписанный,
АВС=
АС;
С
ADC
– центральный,
ADC=
АС.
А
2
)
C
D Углы,
опирающиеся на диаметр прямые.
B
A
АВ – диаметр,
АСВ
=
ADB
=
3)
D
A B
