cСанкт-Петербургский государственный политехнический университет факультет экономики и менеджмента Кафедра информационных систем в экономике и менеджменте

Учебная дисциплина «Математические и инструментальные методы поддержки принятия решений»

ТЕМА 5

Нормативные математические модели и методы СППР

Лектор: профессор АНИСИМОВ Владимир Георгиевич

Санкт-Петербург - 2012

5.1. Общая характеристика нормативных моделей и методов, применяемых в сппр

Нормативные модели и методы в СППР применяются в интересах формирования управленческих решений. Формирование решений по управлению социально-экономической системой или организацией в общем случае может быть представлено отображением

0₁:R  P  S  T  Ц  V, (5.1.1)

где R - множество ресурсов системы;

P - множество потребителей ресурсов;

S - множество возможных ситуаций (состояний социально-экономической системы);

Ц - множество целей, которые должны быть достигнуты в результате управления;

T - множество моментов времени (этапов);

V - множество допустимых вариантов управленческих решений.

Отображение (5.1.1) представляет собой алгоритм, который каждому набору условий (r  R, p  P, s  S, ц  Ц, t  T) ставит в соответствие некоторое решение v V из множества допустимых. Реализация этого решения приводит к некоторому результату, прогнозирование которого при выработке решения может быть в обобщенном виде представлено отображением

0₂:R  P  S  T  V  S. (5.1.2)

Отображение (5.1.2) представляет собой модель, связывающую вариант v  V решения с ожидаемыми результатами s(t  t_o) S использования ресурсов r  R развития социально-экономической системы. При этом качество выбранного варианта v  V определяется конечным результатом использования ресурсов.

Оценка качества в общем виде представляет собой отображение

0₃: R  P  S  T  E, (5.1.3)

где E - упорядоченное по степени предпочтения множество оценок достижения поставленных целей ц Ц.

В совокупности отображения (5.1.2) и (5.1.3) представляют собой модель для оценивания эффективности.

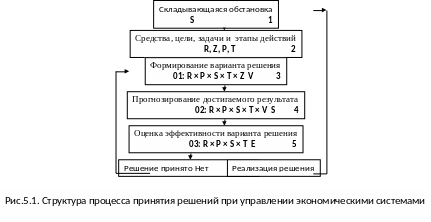
Общая структура процесса формирования решений по управлению может быть представлена в виде рис. 5.1.

На этом рисунке блоки 2 - 5 отражают обобщенную структуру методики формирования управленческих решений.

При моделировании социально-экономического процесса оценка достижения целей, то есть процедура формирования отображения (5.1.3), формально сводится к проверке выполнения некоторых целевых соотношений следующего вида:

H (r, p, s, t) = 0, 

G (r, p, s, t)  0,  (5.1.4)

Q (r, p, s, t)  extr

где H (.) - вектор требований типа равенств;

G (.) - вектор требований типа неравенств;

Q (.) - вектор экстремальных требований.

Если условия (5.1.4) в принципе выполнимы, то добиться их реального выполнения можно только путем изменения результатов процесса s(t  t₀)  S за счет соответствующего подбора элементов решения v  V.

В рамках рассмотренной структуры задача формирования целесообразного варианта решения по управлению может быть формально представлена в виде следующей модели выбора:

Определить вариант решения

v*(r,p,s,t₀)  V, (5.1.5)

для которого выполняется условие

Q(r,p,s,t  t₀,v*) = extr Q, (5.1.6)

при ограничениях

H(r,p,s,t  t₀,v*) = 0, (5.1.7)

G(r, p, s, t  t₀,v*)  0. (5.1.8)

Представление задачи формирования решений по управлению в виде соотношений (5.1.5) - (5.1.8) является обобщенным, но в то же время достаточно содержательным для классификации и выбора на этой основе математического аппарата моделирования и методов нахождения решений. В частности, в зависимости от размерности k₁ вектора Q(.) можно выделить балансные (k₁=0) и оптимизационные k₁>0 модели. В балансных моделях оценивание эффективности не имеет большого значения, поскольку приемлемым считается любое решение по управлению рассматриваемым процессом, обеспечивающее баланс задач и имеющихся ресурсов.

Ключевое значение оценивание эффективности приобретает в оптимизационных моделях, поскольку в них решение формируется на основе сравнения возможных вариантов по ожидаемой эффективности. Модели этого класса в настоящее время уже частично разработаны, но не нашли широкого применения в практике управления. Вместе с тем, будущее за ними, поскольку характерный для современных условий дефицит ресурсов объективно обусловливает необходимость их рационального использования.

При k₁ = 1 оптимизационная модель решения соответствующей задачи будет однокритериальной, а при k₁ > 1 - многокритериальной.

В зависимости от размерностей k₂ и k₃ векторов H(.) и G(.), соответственно, различают класс моделей безусловной оптимизации (k₂ = k₃ = 0) и класс моделей условий оптимизации (k₂ + k₃ > 0).

Размерность i вектора r  R ресурсов определяет классы однономенклатурных (i=1) и многономенклатурных (i > 1) моделей.

В зависимости от учета или не учета параметров t  T различают динамические (многоэтапные, t>1) и статические (одноэтапные t = 1) модели.

По наличию в составе вектора s  S компонентов, характеризующих конкуренцию субъектов и объектов социально-экономического процесса, можно выделить модели с учетом и без учета конкуренции. При этом в зависимости от способа учета конкуренции различаются односторонние и двухсторонние игровые модели.

По степени детерминированности элементов и связей в соотношениях (5.1.5) - (5.1.8) различают детерминированные модели, стохастические модели, а также модели выбора решений в условиях неопределенности.

Все эти особенности находят отражение в средствах математического описания моделей и методах поиска решений. Так, в классе линейных балансных статических моделей используется формальный язык линейной алгебры.

Для класса линейных или нелинейных динамических моделей с непрерывной функцией времени используются, соответственно, линейные или нелинейные дифференциальные уравнения.

Формализация задач принятия решений в виде односторонней статической модели без учета фактора времени обычно приводит к различным типам детерминированных или стохастических одноэтапных задач математического программирования, а в случае учета времени - к многоэтапным (динамическим) задачам математического программирования или краевым и вариационным задачам оптимизации.

Формализация задач принятия решений в виде двухсторонней модели может быть осуществлена в классе игровых моделей, которые также могут быть статическими или динамическими, дискретными или непрерывными, линейными или нелинейными и т.п.

Таким образом, моделирование в интересах формирования решений по управлению социально-экономическими и организационно техническими системами может осуществляться различными способами. Целесообразность того или иного из них определяется сущностью моделируемой задачи, условиями, в которых осуществляется ее решение и совокупностью требований, вытекающих из методологических принципов выбора вариантов построения и комплексирования моделей и алгоритмов оптимизации.